抗滑桩—格构梁联合加固边坡效果分析

赵志强 姚 成

(江苏科技大学土木工程与建筑学院，江苏 镇江 212000)

0 引言

近年来，在土木工程生产实践活动中随着高速公路建设向西部的延伸和发展，涉及了大量的边坡工程技术课题，由于我国西部地区地形，地质条件较为复杂，深挖高填十分普遍，边坡工程问题日益突出。目前国内外滑坡灾害防治技术措施还包括:卸荷、压坡角、坡面防护、抗滑桩、锚杆、预应力锚索、综合加固等方法，在很多大型滑坡灾害防治工程中往往同时采用多种防治措施。针对一些地质复杂，岩性较差，节理发育的土质深路堑边坡，工程中已经开始利用桩打入稳定岩层的预应力锚索抗滑桩阻止山坡整个滑体滑动，外加锚索对格构梁的反拉力来控制滑面的进一步滑动的复合结构。

针对抗滑桩—格构梁联合应用支护边坡，根据预应力锚索抗滑桩变形协调原理，在变形协调中增加格构梁的变形影响。本文借助有限元软件ABAQUS进行建模分析，通过计算结果对比分析，选择更有利于边坡加固的方法。

1 锚索、抗滑桩以及格构梁三者变形协调

若预应力锚索抗滑桩—格构梁复合结构在理论设计中考虑将桩与格构连接作为整体，变形如图1所示。

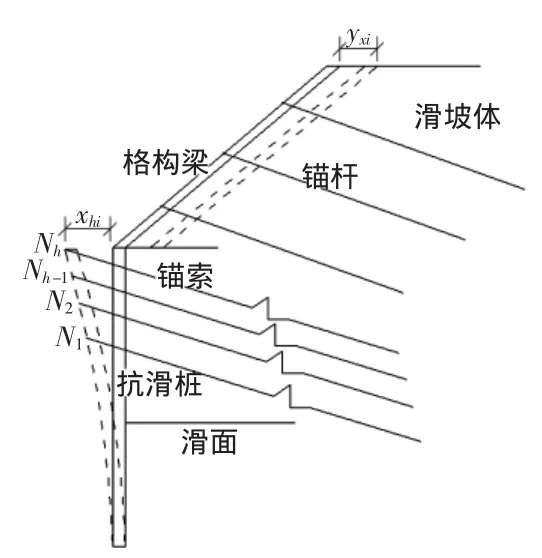
图1 抗滑桩与格构梁联合结构图

滑动面以上桩身的位移为:

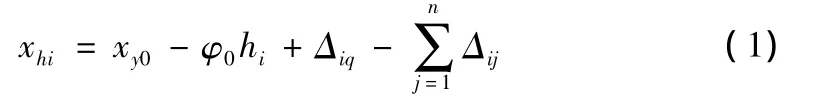
其中，xy0为桩0点处水平位移;φ0为桩0点处转角;Δiq为滑坡推力或岩土压力作用于第i根锚索处桩的水平位移;hi为第i根锚索距离滑坡面的距离;Δij为锚索拉力Ni水平分量作用在第j根锚索的水平位移，Δij=Njcosαjδij(αj为第i根锚索与水平线夹角;δij为锚索拉力Ni水平分量作用在第j根锚索的水平位移系数)。

假定锚索的变形计算不考虑桩的挠曲变形对锚索变形的影响，则锚索在预应力作用下的弹性变形Δli，根据胡克定律得:

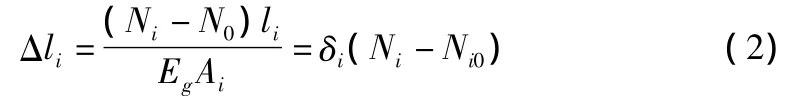
其中，Δli为第i根锚索弹性伸长量;Ni为第i根锚索作用力;Ni0为第i根锚索初始应力;Eg为锚索的弹性模量;δi为第i根锚索的揉度系数;li为第i根锚索自由段长度与1/3锚固段长度之和;Ai为第i根锚索的截面面积。

根据Winkler地基梁理论，假设地基上任一点所受的压应力p与该点的地基沉降y成正比，格构梁整体变形如式(3)所示:

此位移对第i根锚索处桩的水平位移影响值为yxi:

其中，ω为滑坡坡角;H为桩身悬臂端长度;k为基床系数。

可依据锚索抗滑桩的变形协调原理将式中增加格构梁水平位移yxi的影响后变为:

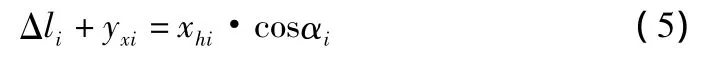
由以上理论分析可知，在锚索拉力相同前提下，考虑桩与格构梁的整体连接与两种结构单独进行计算相比较，前者的位移变形值应更小，对边坡稳定性控制应该会更好。文中的单独结构代表桩、格构梁作为独立结构，复合结构代表将桩与格构梁连接，作为整体考虑。

2 有限元模型

2.1 模型尺寸与材料参数

根据某工程资料，选择滑坡断面，建立边坡体的尺寸为:坡高12 m，坡率选取1∶1;坡前8 m，坡后15 m;选择边坡体采用Mohr-Coulomb弹塑性本构模型，土的力学参数见表1。

表1 土体力学参数

格构梁模型的基本布置方式:横、纵梁的间距均为3 m，悬臂端长度为1.5 m，纵梁和桩通过桩顶连梁连接起来;桩长度为12 m。如前所述，格构梁和桩以及连梁都采用 ABAQUS提供C3D8R类型的实体单元来模拟，有关力学参数见表2。

表2 桩与格构梁力学参数

2.2 荷载与边界条件

该模型主要受重力作用，桩上的锚索拉力以集中力施加在桩顶，大小为200 kN，与水平线夹角为30°;格构锚杆拉力将其简化为锚杆作用在横、纵梁交叉面上的面应力，大小为1000 kPa(约合拉力100 kN)。边界条件为:垂直于x轴的左、右两个面上，没有x方向的位移;垂直于z轴的前、后两个面，没有z方向的位移;垂直于y轴的底面，没有x，y，z三个方向的位移。

3 计算结果分析

3.1 滑坡支护前后安全系数对比

将滑坡支护前后的FV(即安全系数)值随U1(土体水平位移)的变化关系绘于图2中。从图2中可知，滑坡本身的安全系数为0.85左右，为不稳定滑坡，当采取支护结构方案都能提高滑坡的安全系数，并且安全系数值在1.2以上，说明支护结构能提高滑坡的稳定性。

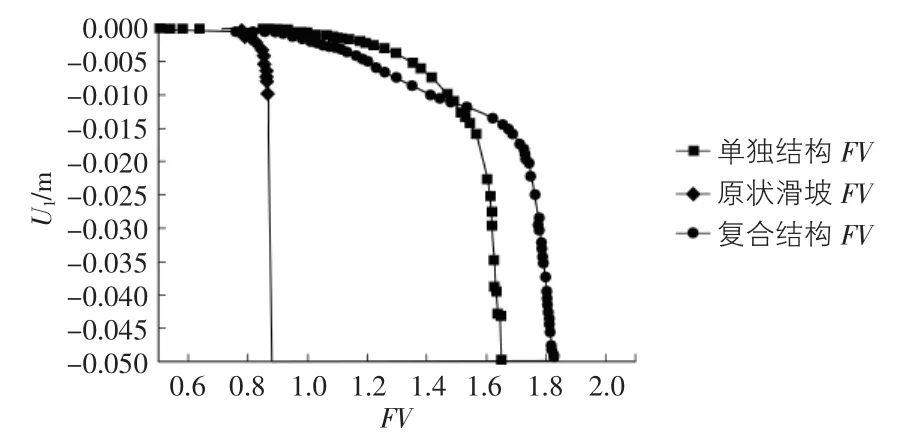
图2 FV随水平位移的变化关系

3.2 支护结构位移分析对比

图3～图6分别给出两种结构土体强度折减到同一数值时的水平位移等值线云图以及整体位移等值线云图。根据强度折减原理在ABAQUS中的实现过程，在计算中止时位移情况如图7～图9所示。

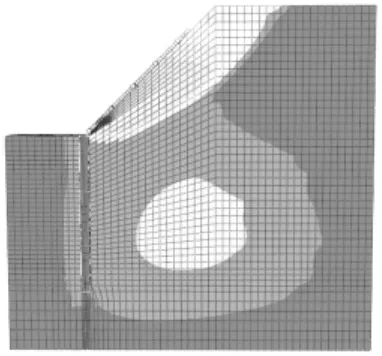
图3 单独结构水平位移等值线云图

图4 复合结构水平位移等值线云图

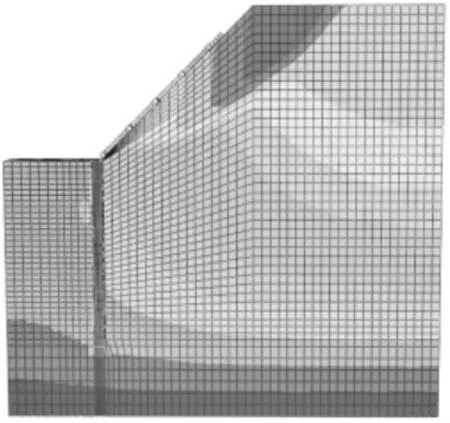
图5 单独结构整体位移等值线云图

图6 复合结构整体位移等值线云图

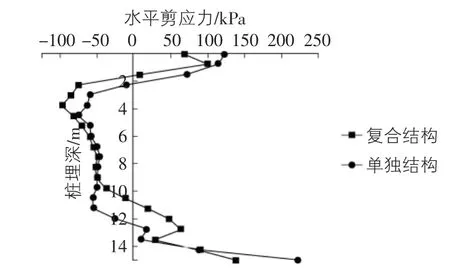
图7 水平剪力随桩埋深分布

从水平位移图以及整体位移图对比可知，单独结构情况下，格构梁对坡体的加固效果影响范围较小，并且局部区域内位移过大;复合结构则在很大程度上体现出对边坡加固的整体性，无论是水平位移等值线云图还是整体位移等值线云图，整个边坡位移变化更均匀。

3.3 抗滑桩剪力分布

图7比较了单独结构和复合结构两种情况下桩身所受水平剪应力的分布情况。计算结构表明，两种结构下的剪应力分布曲线形状存在差异。复合结构的第二个剪力为零点出现在桩顶以下大约10.5 m处，单独结构则出现在12.5 m左右的地方，相比之下，复合结构的桩锚固深度较单独结构情况下更深。剪应力为负代表桩所受剪力为滑坡下滑方向。

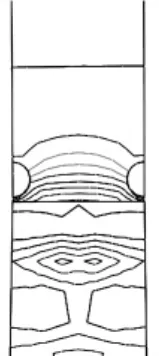
图8 单独结构桩间水平位移等值线图

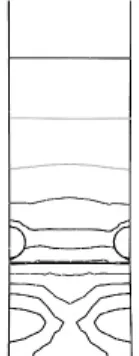
图9 复合结构桩间水平位移等值线图

3.4 桩间土体流失情况对比

图8和图9为桩间水平位移等值线图。从图中可以看出，单独结构等值线图中部出现向x轴负方向的弯曲，说明此时土拱作用已经不太明显甚至消失，土体已经出现绕桩流失现象;复合结构情况下等值线图中部曲线弯曲并未完全趋向x轴负方向，甚至部分还存在向x轴正向弯曲。x轴负向为滑坡破坏方向，在等桩间距条件下，通过x轴方向位移等值线图对比可知，复合结构中还有土拱作用存在。

4 结语

1)抗滑桩—格构梁复合结构整体设计和抗滑桩、格构梁单独结构设计两种方法中，前者提高边坡的安全系数更高，支护后边坡整体位移变化更均匀，支护效果更好。

2)通过对两种情况的桩剪力、桩间土体流失情况对比，对于同一边坡治理问题，在加固效果相同的前提下，考虑将抗滑桩—格构梁作为整体的复合结构可适当增加桩间距或降低桩长，以达到降低工程造价的目的。

[1]陈希哲.土力学地基基础[M].北京:清华大学出版社，2004:316-318.

[2]段智伟.预应力锚索与抗滑桩在高速公路滑坡治理中的应用[J].科技情报开发与经济，2005，15(17):263-264.

[3]桂树强.预应力锚索抗滑桩结构计算方法[J].中国地质大学学报，2005，30(2):223-240.

[4]佴 磊，徐 燕，代树林.边坡工程[M].北京:科学出版社，2010.

[5]李 群，章广成，唐辉明，等.十字交叉格构梁内力分析与优化设计[J].煤田地质与勘探，2006，34(6):50-53.