预应力锚索桩计算理论的研究现状和对其力学模型的探讨

吴润泽 ，周海清，胡源，李鹏举

（1后勤工程学院军事建筑工程系，重庆 401311；2岩土力学与地质环境保护重庆市重点实验室，重庆 401311）

0 引言

从20世纪80年代开始，预应力锚索抗滑桩因其自身的优势而被广泛应用于工程建设中。同传统的抗滑桩相比，由于预应力锚索的设置不仅约束了桩身的变形和位移，也进一步改善了桩体的受力状态，桩身的内力显著减小，从而减小了桩体的截面尺寸、钢筋用量和锚固深度，桩间距也得以加大，一定程度上节约了工程造价。

虽然预应力锚索桩广泛应用于滑坡整治工程，但它的力学计算模型以及相应的计算理论却并不完善，在某些方面并不能反映其真实的工作状态和力学机理，尚未得到业界公认。

1 国内锚索桩计算理论的研究现状

国内学者对锚索桩的研究较为活跃，也取得了一定的成果，比如陈占结合梁挠曲变形微分方程和地基系数法,采用分段计算法计算了预应力锚索桩桩锚协调变形时桩的变形与内力[1]。周德培将桩简化为受约束的弹性地基梁,结合桩锚变形协调原理,按地基系数法求取锚索拉力和桩身内力[2]。杨佑发基于地基系数“K-K”法的原理，运用有限差分法对预应力锚索抗滑桩全桩内力进行了计算[3]。桂树强将双参数法引入地基系数并贯穿到整个桩身结构计算[4]。但这些研究都是在锚索桩内力的求解方法上或不同地基模型上做文章，只是数学上的不同，而不是对锚索桩真实受力规律的探索，计算所采用的力学模型都是在普通抗滑桩力学模型的基础上引入桩锚协同变形条件，增加了锚索对桩的约束条件，这样仅能反映锚索桩是一种受约束的抗滑桩，却未能反映锚索桩主动式受力这一重要力学过程。刘小丽针对这一力学过程，提出了预应力锚索桩改进计算的新方法，考虑了锚索预应力张拉阶段对桩后土体的预加固作用并反映到其计算模型中[5]，但尚不完善，还处于探索阶段。

2 桩锚协同工作机理分析

预应力锚索桩的施工和受力过程大概可划分为以下三个阶段[6]：

第一阶段为桩身、锚索的施工阶段。抗滑桩与锚索施工完毕，预应力尚未施加，边坡处在稳定状态，此时桩身的作用力较小，锚头处的侧向位移也近似为零。本文认为此阶段不需单独建立锚索桩的力学模型进行内力计算，但此时锚索张拉前桩侧的岩土压力是否会影响到后续桩身内力的计算还需要进行大量的系统研究来论证。

第二阶段为预加固阶段。张拉锚索施加预应力并锁定，张拉力通过锚索锚固段传至稳定岩层中，抗滑桩在锚索拉力的作用下将绕下部的某个位置发生一定量的整体转动，滑面以上桩体将对其背后的土体形成挤压起到加固边坡的作用，桩和背后土体之间自然也就产生了相互作用的力，此时滑动面以上桩体的受力特点类似于弹性地基梁，而这一重要的力学过程正是预应力锚索抗滑桩所特有的，它必将对桩身内力计算产生重要影响，现有的锚索桩力学计算模型都未能准确反映这一力学过程所产生的影响，如何准确地分析这一过程，建立真实的计算模型，将这一阶段带来的影响反映到计算理论中，关系到一套合理的锚索桩计算理论体系的建立。

第三阶段为滑坡推力逐渐作用直至完全施加到桩上。随着时间的推移，由于坡体前部的开挖或者降雨等不利因素的影响，滑坡推力增大并逐渐作用于桩上，桩体会向远离滑坡体的方向发生侧移和转动，此阶段桩和锚索将作为一个整体来起到稳定边坡的作用，桩的侧向变形要受到锚索的弹性约束，锚索拉力由于桩体的变形而会增大到设计值，桩与锚索之间存在变形协调关系。

3 预应力锚索桩计算模型的三个重要环节

目前预应力锚索桩的计算模型主要是将桩体从滑动面位置分为上下两段，上段视为具有弹性支座的简支梁，在考虑桩身与桩后滑体的相互作用时，常是将滑坡推力以某种可能的分布方式作用于桩身悬臂段，其分布不受桩与背后岩土体相互作用的影响，国内对于这种固定的分布方式的研究也取得了一些总结性的成果[7]；下段视为弹性地基梁，对于滑面以下的岩土体与桩的相互作用则采用弹性地基梁理论，同时对于滑面以上桩前有抗体的情况，剩余抗滑力可采用以某种分布形式作用于桩上，也可与桩锚固段岩土体作为一个整体按弹性地基梁理论考虑。本文认为建立一个合理、真实、完整的预应力锚索桩力学计算模型，以体现出预加固阶段的特有影响，离不开对以下三个环节的考虑，这将直接影响到锚索桩结构的内力计算。

3.1 滑坡推力的分布形式

滑坡推力分布形式受滑坡类型，地层性质等多种因素的影响，确定起来十分困难。戴自航结合模型试验和现场实测在其论文中对不同岩土类别总结出了不同形状的推力分布形式，并给出了相应的分布函数[7]。目前不论是普通抗滑桩还是预应力锚索桩，人们在工程中都参照这些分布形式结合自身经验对其进行设计计算，但锚索桩比普通抗滑桩多一个施加预应力的主动受力阶段，在这一阶段，锚索预应力的预加固作用显然将改变滑动面以上桩体背后岩土压力的分布，位置越靠上，桩的侧移越大，挤压作用越明显，桩背后的岩土压力就越大，而这种改变的影响还会持续到锚索桩的第三受力阶段，改变最后的滑坡推力分布形式。这种影响的程度大小与所施加的预应力的大小有关，施加的预应力越大，影响就越明显。因此锚索桩最终的滑坡推力的分布形式与所施加的预应力的大小是相关的，照搬普通抗滑桩固定不变的滑坡推力分布形式进行设计计算显然是不合理的，不过预应力大小与滑坡推力分布形式之间具体的影响规律还需要通过系统地试验研究才能了解。

3.2 桩锚变形协调方程

桩锚变形协调方程是求解锚索拉力的关键，但目前文献中提出的桩锚协调变形条件都存在明显不足。有文献认为锚索的伸长量等于桩锚连接处桩的水平变形量，明显忽略了锚索与水平方向存在的夹角，也没有考虑桩身在滑面处存在转角和位移[8]。有文献考虑了这些，认为锚索的伸长量与桩锚连接处桩身的水平位移在沿锚索方向的分量相等，但该方法认为桩在最终的滑坡推力作用下是沿竖直位置向坡体外侧位移，忽略了桩身在预应力作用下已经产生了向坡体内侧的位移[4]。后来毛明章在其提出的桩锚协调变形方程中加入了桩身在预应力作用下向坡体内侧的位移，但其这部分位移只考虑了桩身在滑面处的转角和位移对桩锚连接点产生的位移，忽略了桩自身的挠曲变形[9]。

本文所建立的桩锚协调变形方程为：

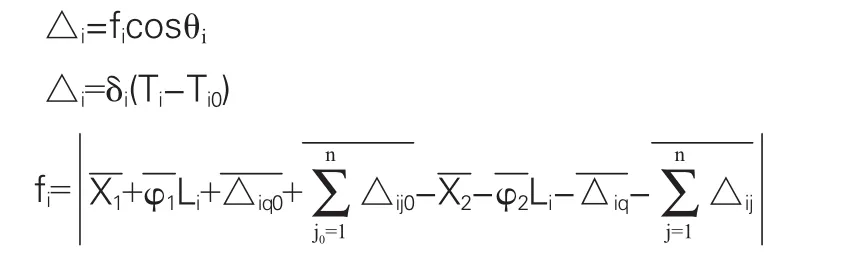
图1 桩锚变形协调示意图

变形协调示意图如图1所示，方程式中：△i为锚索的伸长量；Ti0为锚索的初始预应力；Ti为锚索拉力设计值；δi为锚索的柔度系数；θi为锚索与水平方向的夹角；fi是桩从预加固阶段的位置变化到滑坡推力完全作用于桩身上的位置过程中桩锚连接处水平位移大小为矢量，分别是预应力施加阶段和滑坡推力作用到最大阶段桩身在滑面处偏离竖直方向的水平位移量，以向土体侧位移为正，背离土体侧位移为负是预应力施加阶段和滑坡推力作用到最大阶段桩身在滑面处偏离竖直方向的转角，以顺时针偏转为正，逆时针偏转为负分别为预加固力和滑坡推力完全作用时第i根锚索桩锚连接处的水平挠曲变形量，以向土体侧为正，背离土体侧为负，其中预加固力可将桩视为弹性地基梁求取则分别为各层锚索预应力和各层锚索最终拉力作用时第根锚索桩锚连接处的水平挠曲变形量，以向土体侧为正，背离土体侧为负。

3.3 锚索预应力的取值

大量工程实践表明过大的预应力会使桩体外侧长期受拉，产生过大的负弯矩，增大外侧的配筋量，造成不必要的浪费；而预应力过小则使得锚索应有的作用无法体现。目前预应力的计算方法主要有以下几种 （这里只包含考虑了桩锚协调变形的情况）：

（1）假设锚索预应力考虑为锚索设计拉力的4/7等经验值，代入桩锚协调变形方程进行计算，不过计算出的锚索预应力和设计拉力应根据桩顶位移控制标准进行校核使桩身受力合理[1]。

（2）根据滑坡推力和锚索拉力使得桩身正负弯矩大致相等的条件求解锚索拉力设计值，再代入桩锚协调变形方程求解预应力[11]。

除此之外，其他学者也提出了一些自己的计算方法，比如刘小丽提出按长期荷载作用确定锚索的预应力[6]；郑明新认为预应力可取滑坡推力的0.43倍[12]。总之这方面还需要大量进一步的研究，工程设计中应根据现场具体情况，综合考虑选取最合理的方式来确定锚索预应力,不必在任何时候都采取相同的计算模式。

4 结语

文章通过对桩锚协调变形机理的分析，将预应力锚索桩按照施工和受力过程划分为三个阶段，认为锚索桩是一种“主动式受力结构”，仅仅采用在普通抗滑桩计算模型基础上作简单修改后得到的模型进行计算是不合理的，预应力的施加必然对桩后岩土压力的分布形式产生直接的影响，进而影响到桩身内力的计算。同时本文还探讨了预应力锚索桩计算模型包含的三个重要环节，提出了更加合理的桩锚协调变形方程。目前预应力锚索桩的计算理论还远滞后于工程实践，还需要大量系统性的研究来提高锚索桩设计的可靠性和合理性，使其在工程中得以更好地应用。

[1]陈占.预应力锚索桩设计与计算[J].地球科学——中国地质大学学报，2001，26(4)：352-356.

[2]周德培，王建松.预应力锚索抗滑桩内力的一种计算方法[J].岩石力学与工程学报，2002，21(2)：247-250.

[3]杨佑发，许绍乾.锚索抗滑桩内力计算的有限差分“KK”法[J].岩土力学，2003，24(1)：61-64.

[4]桂树强.预应力锚索抗滑桩结构计算方法[J].地球科学——中国地质大学学报，2005，30(2)：233-240.

[5]刘小丽，张占民，周德培.预应力锚索抗滑桩的改进计算方法[J].岩石力学与工程学报，2004，23(15)：2568-2572.

[6]刘小丽.新型桩锚结构设计计算理论研究[D].西南交通大学，2003.

[7]戴自航.抗滑桩滑坡推力和桩前滑体抗力分布规律的研究[J].岩石力学与工程学报，2002，21(4)：517-521.

[8]黄质宏，郭建强，张建，等.关于预应力锚索抗滑桩内力计算方法的讨论[J].贵州工业大学学报：自然科学版，2008，37(1)：72-76.

[9]毛明章，邹先锋.预应力锚索抗滑桩协同工作机理[J].地下空间与工程学报，2010，6(增刊2)：1552-1555.

[10]邹兴普.锚索抗滑桩的设计计算[J].路基工程，2000，(2)：9-11.

[11]郑明新.预应力锚索抗滑桩中预拉力合理值的探讨[J].力学与实践，2011，33(5)：16-20.