纯转动拉曼测温激光雷达滤光器参数设计

马征征 王晓宾 康士峰 吴 健

(中国电波传播研究所 电波环境特性及模化技术重点实验室，山东 青岛 266107)

引 言

纯转动拉曼测温激光雷达是一种探测低层大气温度的先进设备。其利用大气分子(主要是氮气和氧气)拉曼散射谱形所具有的温度依赖关系，来反演大气温度参数。纯转动拉曼测温激光雷达除了具有激光雷达所共有的即时性、连续性、遥测等优点外，还具有不受气溶胶和薄云影响的优势。目前，纯转动拉曼测温激光雷达的测量范围多为近地面至对流层中部(3～5 km)，这一区域的大气温度参数具有科研、气象、生产、生活等多方面的意义[1]。

然而， 目前纯转动拉曼测温激光雷达主要还用于科学研究领域，其系统设计并无明显针对性。近年来，随着激光雷达探测技术的发展，针对大气波导探测的拉曼激光雷达逐渐提到议事日程上来。该技术采用振动拉曼技术测量大气湿度，采用纯转动拉曼技术测量大气温度[2]。所谓大气波导，是指当大气折射率梯度满足一定特殊条件时，电磁波射线被限制在一定厚度的大气层内(下边界也可以是地/海面)上下反射向前传播，此时电磁波能够在较小衰减下传播得很远。按出现高度划分，包括悬空波导和表面波导。其中，悬空波导出现概率较低，出现高度从近地面至3 km，而表面波导出现高度贴近地面(100 m以下)。在海洋或大面积水域环境下，容易出现一种被称为蒸发波导的特殊表面波导，其出现概率超过50%.虽然大气波导本身的温度变化范围并不大，但由于其垂直结构非常精细(可小至几米)，对温度的探测精度提出了很高要求[3]。

传统的大气波导探测主要采用无线电探空仪。与其相比，目前纯转动拉曼激光雷达对温度的探测精度大体上要略低一些[2]。根据分析，其误差来自以下多个方面：首先，激光雷达探测大气参数的基本载体是光子。虽然激光器发射的初始光子数非常巨大(如1020个)，但事实上最终能接收到的光子数十分有限(如103个)。最主要的损失来自于被探测体极小的散射截面和望远镜对散射体所张的极小的接收立体角。因此，反演结果不能忽视回波信号起伏引起的误差。第二，纯转动拉曼激光雷达是通过选取散射谱上具有不同温度依赖关系两处的回波比对，来提取温度信息。因此，探测精度与选取处有直接关系。此外，还有拟合公式、背景噪声、弹性信号(瑞利和米散射)混入、定标误差等都会造成测量误差[1]。

综合上面的分析，不难发现，纯转动拉曼激光雷达滤光器件参数的选择具有相当重要的意义。一方面，其直接决定了回波与温度的依赖关系，决定了探测误差；另一方面，其还决定了接收的信号和噪声光子数，从而影响测量信噪比和探测误差。目前，多数纯转动拉曼激光雷达并无明显针对性，其滤光器件参数的设定要求较为宽松[4-8]。然而，对于大气波导，鉴于其精细的垂直结构，对温度的探测精度提出了较高要求。同时，不同的探测环境和条件对滤光器参数设计也提出了不同要求。例如：不同地理位置大气及波导温度不同，悬空波导和蒸发波导温度不同，夜间或白天温度和背景噪声不同等。在这种情况下，有必要针对大气波导的特殊要求来设计纯转动拉曼测温激光雷达的滤光器参数，以获得最优化的探测精度。以下我们将通过理论和仿真研究滤光器件参数对测量温度误差的影响，为高精度拉曼测温激光雷达系统的设计作参考。

1 理论原理

目前，鉴于掺钕钇铝石榴石(Nd:YAG)固体激光器的技术成熟和广泛使用，纯转动拉曼激光雷达最常采用的发射波长为二倍频532 nm和三倍频354.7 nm，其中后者具有更高的后向散射截面和对人眼的安全性而更广泛地被采用[4-8]。参考我所振动拉曼激光雷达的硬件参数[9]，以下的研究中我们设定激光器脉冲频率为20 Hz，在354.7 nm波长时脉冲能量为300 mJ，观测积累时间为5 min.于是发射光子总数为

(1)

此外，接收望远镜直径为0.5 m，假设重叠因子为1，雷达效率简单设定为1%[10].对悬空波导的探测，高度分辨率设置为30 m；而对于蒸发波导的探测，高度分辨率为3 m.

1.1 消 光

光子的消光过程包含分子消光和气溶胶消光。分子消光主要是由氮气和氧气的瑞利散射引起的，相对容易计算，根据量子力学知识，瑞利微分后向散射截面计算式为[1]

(2)

式中： 下标i代表氮气或氧气分子；ν0是激光的波数，其他部分参量如表1所示。而分子的消光系数可由后向散射截面和消光后向散射比(8π/3)得到，氮气和氧气密度剖面可由大气模式得到。

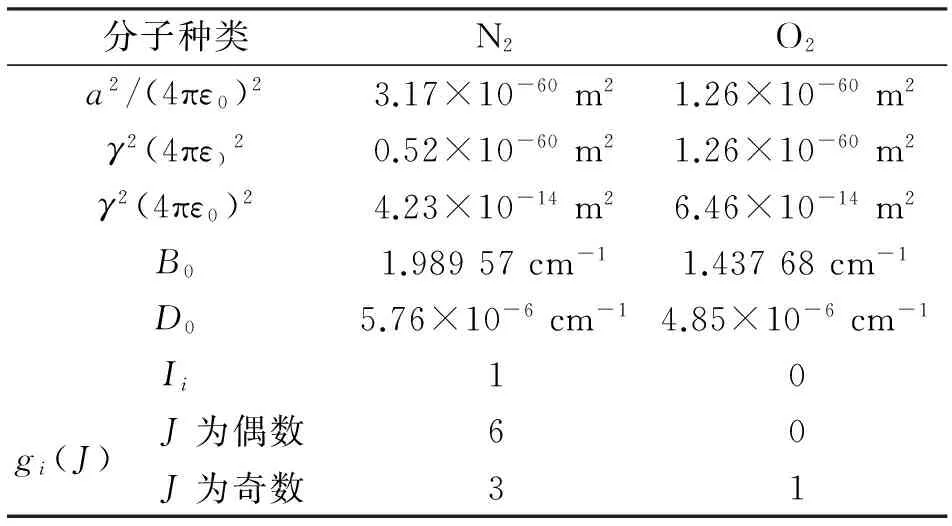
表1 有关瑞利散射和拉曼散射的部分参数表

对于大气气溶胶，本身存在较强的时变性，其消光系数平均值可由模式[11]得到：

aa(z)= 0.025(1+0.4)2ez/1.6/(0.4+ez/1.6)2+

1.5×10-7(1+2 981)2ez/2.5/

(2 981+ez/2.5)2

(3)

对于气溶胶尺度大于波长的情况，气溶胶消光系数与波长无关[12]。

1.2 散 射

根据量子力学理论[1]，氮气和氧气分子的转动能级为

Ei(J)= [B0,iJ(J+1)-D0,iJ2(J+1)2]hc0,

J=0,1,2,…

(4)

J为转动能级数，斯托克斯和反斯托克斯拉曼频移为

ΔνSt,i(J)= -B0,i2(2J+3)+

(2J+3)3],D0,i[3(2J+3)+

J=0,1,2，…

Δνan-St,i(J)=B0,i2(2J-1)-

D0，i[3(2J-1)+(2J-1)3],

J=2,3,4,……

(5)

拉曼后向微分散射截面为

(6)

其中部分参量由表1给出，另外，

(7)

MSIS-E-90(地面至热层中性大气密度和温度)模型[13]给出的青岛(120°E，36°N)上空0～5 km高度温度范围约为250～300 K.因此，根据式(6)计算得到氮气和氧气在250 K和300 K下纯转动拉曼散射截面谱，如图1所示。注意到虽然氧气的拉曼散射截面更大，但大气中氮气的含量要高一些。

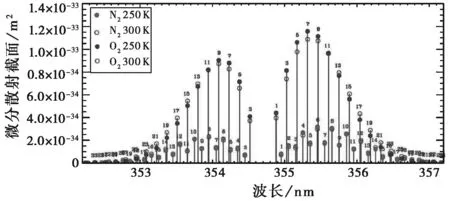
图1 发射波长为354.7 nm时氮气和氧气250和300 K下纯转动拉曼散射截面谱

1.3 反演方法

雷达方程为

(8)

式中：S0为发射光子数；ε为雷达探测效率；Α为接收望远镜物理面积；O(z)为重叠因子；N(z)为被探测物数密度；τ(Ji)为波长对应滤光透过率；ηi为相对丰度比；τa(z)为大气透过率。根据拉曼测温方法，两个通道接收的回波光子数比值为

(9)

认为两个通道具有相同的雷达效率，而两个通道的接收波长非常接近，可认为具有相同的大气透过率[1]。代入雷达方程有

(10)

对于简单情况，两个通道可以分别仅选取单支谱线，由式(6)和(10)，很明显可确定Q与T的关系：

Q(T)=exp(a-b/T)

(11)

于是有

(12)

式中，常数a和b需要定标。通常通过其他测温手段同步测量的T，来得到a和b的值。

事实上，虽仅包含一支谱线但会对滤光器件提出较高的技术要求(带宽需小至pm量级)[14]，并且鉴于单支谱线有限的散射截面，此时回波信号强度并不高，也就对应较高的探测误差[15]。当滤光器件包含多根谱线时，Q与T的关系将与式(11)背离，产生较大误差。然而，通过理论计算来获得两者的准确关系式较为复杂，并且滤光器件的参数也难以被准确获得。因此，实际操作中通常都不采用理论计算，而采用拟合方法。一种直观的提高测量精度方法就是在式(12)中增加二阶关系。类似地，还可以增加三阶关系来进一步提高探测精度。一种增加二阶关系的方式为

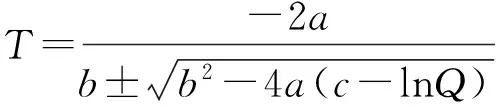
(13)

该公式的好处是仅有三个待定参数。同时据研究，该式在多数时候的拟合精度很高。因此，该式被广泛用于纯转动拉曼雷达的温度反演中[1]。

2 理论与仿真结果

2.1 温度对探测精度的影响

计算无噪声情况下滤光器件中心波长和带宽(半高全宽)的选取对探测精度的影响。对于温度T(Q)，根据传递公式，其标准差为

(14)

而由式(9)得

(15)

无噪声情况下，两个通道的信号服从泊松分布，有

(16)

于是，最终有

(17)

式中，分母项大体表示两个通道回波强度随温度变化的差异。直观上认为，若一个通道回波强度随温度升高而增强，另一个通道回波强度随温度升高而减小，则分母具有较大值，探测的温度具有较高精度。但也需注意式(17)分子项大体表示了回波泊松分布对测量精度的影响，较高的回波强度对应了较小的探测误差。因此，两通道即使具有相反的温度依赖关系，但若具有较低的回波强度，也可能具有低的探测精度。

根据大气模式，青岛地区2 km高度处(悬空波导高度)平均大气温度约为280 K.通过仿真计算来考察2 km高度处280 K时的温度测量误差。有4个自变量：一号通道滤光器件的中心波长和半高全宽，二号通道滤光器件的中心波长和半高全宽。采用嵌套循环的方式，来仿真计算4个自变量不同取值时的温度标准差。参考图1给出的谱线强度与温度依赖关系，一号通道滤光器件中心波长范围为353.7～354.6 nm，步长为0.1 nm；二号通道滤光器件中心波长范围为352.7～353.6 nm，步长为0.1 nm(为避免气溶胶荧光的影响，通常都选用拉曼散射的反斯托克斯谱)。两通道半高全宽范围均为0.1～1.0 nm，步长为0.1 nm.转动拉曼谱计算得到，事实上此时的后向微分散射截面已低于10-40m2.对滤光器件透过率随波长的分布使用高斯形函数来模拟，假设两通道滤光器件的峰值透过率均为100%.另外，所选滤光片在发射波长处还应达到较高的截止率，约107[1]。于是通过式(8)，可以计算得到S1和S2.再通过式(17)，计算得到σ(T)最小值为0.31 K，此时两通道滤光器件参数如表2所示。

表2 无噪声情况下滤光器件的参数选型

而对于蒸发波导的探测，探测高度设定为96 m，该高度上大气温度平均为290 K.计算得到最小值为0.037 K，出现最小值时两通道滤光器件参数同表2所示。示意图如图2(见1061页)所示，氮气和氧气的散射谱已由各自的数密度加权。

类似地，对多个温度分别计算获得对应的滤光器参数设定最优方案，从而给出随温度变化的滤光器参数设定方案(图3(见1061页))。可见，按照最优方案，温度升高时，二号通道滤光器件中心波长的设计应逐渐远离发射波长；而一号通道滤光器参数设计无变化。

2.2 噪声对探测精度的影响

注意到图2中二号通道的滤光片宽度较宽，实际上其包含的如351.7～352.5 nm范围内的信号很弱。很明显，在考虑噪声的情况下这种配置并不一定优化。通过实验观测简单调查了噪声的强度。图4(见1062页)是利用氮气振动拉曼激光雷达观测得到的回波光子剖面。

观测时间为2008年12月17日22:15 LT，发射波长为532 nm，脉冲频率为 20 Hz，脉冲能量为50 mJ，积累时间为250 s，高度分辨率为30 m.滤光片中心波长为607 nm，带宽为5 nm.蓝色为激光雷达观测的原始结果，红色为用1 km平滑的结果。得到的该模式下背景噪声平均值(20 km以上)仅为3个光子。这表明：对于夜间观测，即使是5 nm宽的滤光片，在采用光子计数模式下，其引入的噪声水平是相当低的。

根据以上分析，对于夜间观测的拉曼测温激光雷达，其滤光器件完全可按表2设计。而对于白天观测，太阳及天空会引起噪声的显著增加。更鉴于探测大气波导的激光雷达必须具有全天时观测能力，考虑噪声存在时，滤光器件参数的选型方案。对于噪声，认为其在355 nm附近均匀分布，因此其强度正比于滤光器件带宽。以下噪声的度量标准为每0.1 nm波长范围内噪声光子个数(100%透过率时)。根据脉冲激光雷达系统的参数反演方法，通常是取时延足够大(距离足够远)处一定范围内平均光子数为噪声水平，再从信号中将其减去。如此，噪声具有的起伏仍将被保留。对于噪声，其也服从泊松分布[16]，于是对除去噪声后的信号有

σ(S′) =σ(S+N-E(N))

(18)

于是有

(19)

计算结果(2 km高度，280 K)如图5(见1062页)所示，红色为1通道滤光器件参数，蓝色为2通道滤光器件参数，使用左坐标轴；黑色为测量温度的标准差，使用右坐标轴。

在噪声存在时，可根据噪声的不同强度选择相应的滤光器件参数方案。当噪声水平低于103个每0.1 nm时，滤光器件参数选取方案一样，只是测量的温度误差略有增加。当噪声水平继续提高时，二号通道滤光器件中心波长的设计需向发射波长靠近。当噪声达到105个每0.1 nm时，二号通道信噪比已低于1，因此不再计算。

2.3 拟合公式对探测精度的影响

除了信号泊松起伏和噪声对测量误差的影响，计算拟合式(13)引起的测量误差，以作参考比对。按照表2使用的配置参数来计算拟合式(13)引起的误差。为单独考虑拟合式(13)所引入的误差，忽略光子的泊松起伏。图6是采用式(13)并在270～300 K之间(悬空波导高度大气温度约为280 K，蒸发波导高度大气温度约为290 K)每1 K取一个点分别得到Q与T的数组(31个元素)， 将两个数组用最小二乘法拟合解出a、b和c，再计算该a、b和c值在各温度下所引入的误差。可见，使用式(13)拟合所引入的误差仅为±0.01 K，相比信号泊松起伏和噪声引入的误差要小得多。

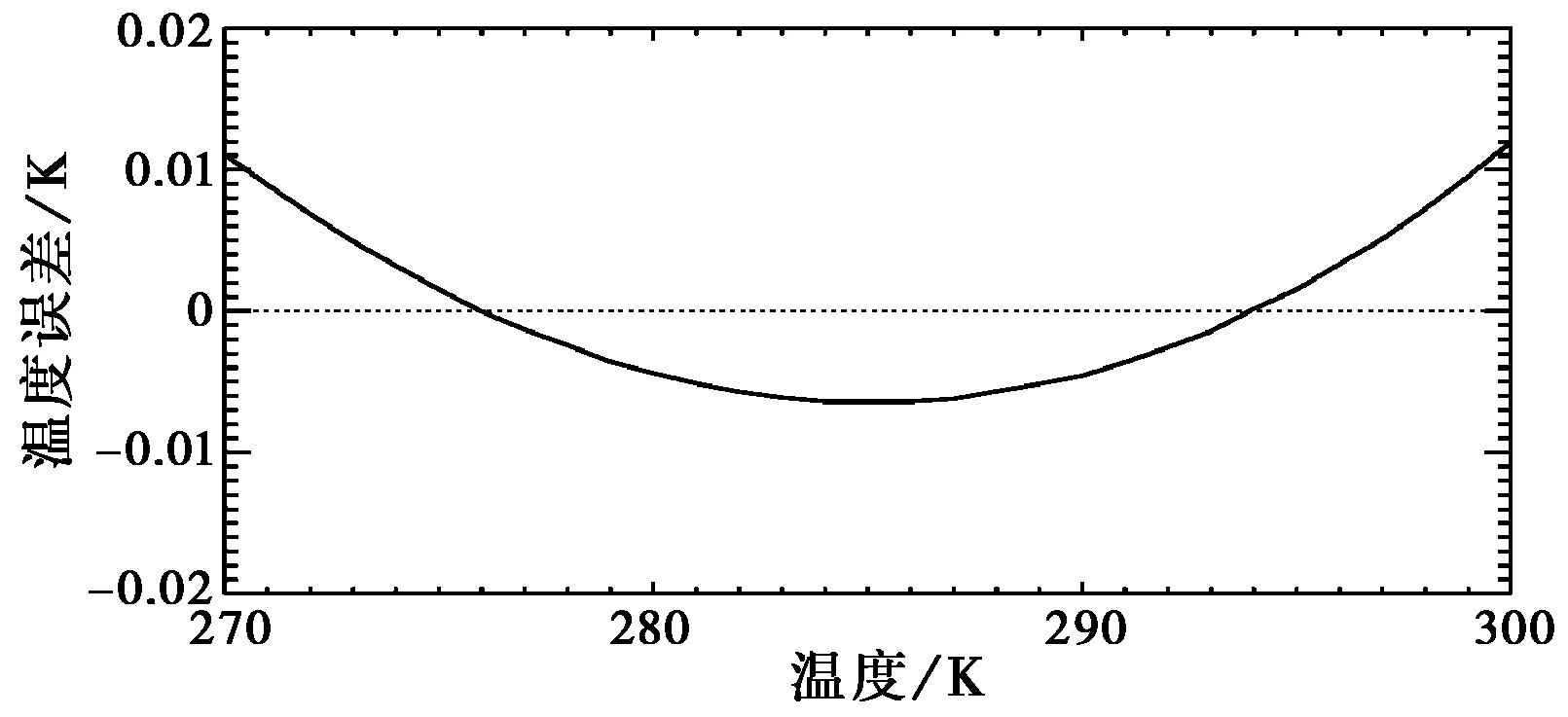
图6 拟合式(13)所引入的测量误差

2.4 弹性信号对探测精度的影响

对于弹性信号，其本身也是噪声的一种。但由于其强度随探测高度的分布并不明确，因此难以被拟合出来而去除。正常情况下都应该从硬件上保证对其较高的截止率(107)[1]。弹性信号包括分子的瑞利散射和气溶胶粒子的米散射，计算测量标准差随瑞利信号透过率的变化，系统参数同上。作为简单考虑，通道各含单支谱线，一号和二号通道分别对应氮气的J=4和J=14谱线。实际中离发射波长更近的一号通道更易混入弹性信号，忽略二号通道内的弹性信号。对于2 km高度，温度为280 K时，结果如图7所示。可见，瑞利信号混入对温度标准差的影响并不明显，但当透过率超过10-7时(拉曼信号透过率设定为1)，其会造成反演温度的显著漂移，必须避免这种情况的出现。

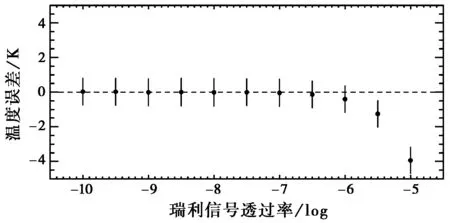
图7 瑞利信号引入的温度测量误差

3 结 论

综合本文的分析，对于354.7 nm发射波长的纯转动拉曼测温激光雷达系统，在给定的典型系统配置下，若噪声水平低于103个每0.1 nm，大气温度为280～300 K时，则两个通道滤光器件参数的最优设计方案为：一号通道中心波长为354.2 nm，半高全宽为0.2 nm；二号通道中心波长为352.8 nm，半高全宽为0.8 nm.此时2 km高度探测的温度标准差为0.31 K，96 m高度处温度标准差为0.037 K.随被探测大气温度的降低，二号通道滤光器件中心波长的设计应逐渐靠近发射波长。对于白天或大噪声水平下的观测，二号通道滤光器件中心波长设计应向发射波长处适度调整。另外，拟合公式引入的误差仅为±0.01 K，可以忽略。最后，弹性信号透过率低于10-7时，对测量结果及误差基本无影响。必须避免混入的弹性信号增大到一定程度后，将引起测量温度的漂移。

[1] WEITKAMP C. Lidar: Range-resolved Optical Remote Sensing of the Atmosphere[M]. New York: Springer: 102.

[2] AGNEW J. Lidar measurement of tropospheric radio refractivity [R/OL].[2011-12-08] http://www.ofcom.org.uk/static/archive/ra/topics/research/rcru/project41/finalreport/d41-6freport.doc

[3] 戴福山, 李 群, 董双林, 等. 大气波导及其军事应用[M]. 北京: 解放军出版社, 2011.

[4] PHILBRICK R. EM & EO properties of the lower atmosphere[C]//BACIMO 2003 Conference. Monterey,September 9-11 2003.

[5] FROIDEVAUX M, SERIKOV I, BURGOS S, et al. A new lidar for water vapor and temperature measurements in the atmospheric boundary layer[J]. Asia Flux Newsletter, 2009(28): 13-17.

[6] BEHRENDT A, NAKAMURA T, ONISHI M, et al. Combined Raman lidar for the measurement of atmospheric temperature, water vapor, particle extinction coefficient, and particle backscatter coefficient[J]. Applied Optics, 2002, 41(36): 7657-7666.

[7] FELTZ W F,SMITH W L,KNUTESON R O, et al. Meteorological applications of temperature and water vapor retrievals from the ground-based atmospheric emitted radiance interferometer (AERI)[J]. Journal of Applied Meteorology, 1998, 37(9): 857-875.

[8] MAO Jiandong, HUA Dengxin, WANG Yufeng, et al. Accurate temperature profiling of the atmospheric boundary layer using an ultraviolet rotational Raman lidar[J]. Optics Communications, 2009, 282(15): 3113-3118.

[9] 马征征, 王晓宾, 康士峰, 等. 青岛地区气溶胶的激光雷达观测[J]. 电波科学学报, 2011, 26(增刊): 344-347.

[10] POVEY A C. Development of an optimal estimation retrieval scheme for a Raman lidar system[R/OL]. [2011-12-08] http://www.atm.ox.ac.uk/group/eodg/1st_year_reports/adam_povey.pdf

[11] SPINHIRNE J D. Micro pulse lidar[J]. IEEE Trans Geo Rem Sens, 1993, 31(1): 48-54.

[12] ANSMANN A,WANDINGER U, RIEBESELL M, et al. Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter lidar[J]. Applied Optics, 1992, 31(33): 7113-7131.

[13] MSIS-E-90 Atmosphere Model[DB/OL]. [2011-12-08]. http://omniweb.gsfc.nasa.gov/vitmo/msis_vitmo.html

[14] 汪少林, 苏 嘉, 赵培涛, 等. 基于三级Fabry-Perot标准具的纯转动拉曼测温激光雷达[J]. 物理学报, 2008, 57(6):649-655.

WANG Shaolin, SU Jia, ZHAO Peitao, et al. A pure rotational Raman-lidar based on three-stage Fabry-Perot etalons for monitoring atmospheric temperature[J]. Acta Physica Sinica, 2008, 57(6): 649-655. (in Chinese)

[15] 苏 嘉, 张寅超, 胡顺星, 等. 多条转动拉曼谱线雷达测量对流层大气温度[J]. 光谱学与光谱分析, 2008, 28(8): 1781-1785.

SU Jia, ZHANG Yinchao, HU Shunxing, et al. Raman lidar measuring tropospheric temperature profiles with many rotational Raman lines[J]. Spectroscopy and Spectral Analysis, 2008, 28(8): 1781-1785. (in Chinese)

[16]H FFNER J, VON ZAHN U. The 1996 Leonid shower as studied with a potassium lidar: Observations and inferred meteoroid sizes[J]. Journal of Geophysical Research, 1999, 104(A2): 2633-2643.