基于混合计算方法的脉冲超宽带穿墙散射建模

任晶晶 柴守刚 陈卫东

(中国科学技术大学电子工程与信息科学系，安徽 合肥230027)

引 言

冲激/脉冲超宽带(IR-UWB)信号具有良好的穿透能力、精确的测距能力以及抗多径和干扰等优势，因此IR-UWB技术是穿墙环境中目标探测与数据通信的优选体制。在室内穿墙应用中，墙体和室内物体对IR-UWB信号传播的影响是超宽带系统设计必须考虑的重要因素，因此通过电磁建模来研究墙体和室内物体的IR-UWB信号传播与散射特性是十分必要的。由于墙体和室内物体是包含电大与电小两类尺寸的混合结构，所以在研究其反射、透射、绕射以及散射等传播现象时，需要采用能兼顾电大电小结构的混合电磁计算方法。在电大结构计算中，混合方法应着重考虑满足工程精度的高效计算问题；而在电小结构计算中，应优先考虑混合方法的计算精度和稳定性。

时域有限差分方法(FDTD)方法是一类可以精确分析IR-UWB信号室内传播过程的有效方法，在低频、复杂结构的建模问题和源设置上都优于伪谱时域法(PSTD)，因此在超宽带(UWB)室内场景的建模上应用较多。但是它需要对计算区域进行细致的网格剖分，以满足数值色散对空间离散间隔的要求，计算量较大。对于大尺度环境的电磁计算，人们通常采用高频近似的数值分析方法，其中射线追踪[1-2](Ray-tracing)技术以几何光学(GO)为基础，具有计算内存需求小、运算速度快的优点，并且易于和其他电磁数值计算方法混合使用[3]。在传统射线追踪算法中，需将激励源表示成傅里叶积分，根据场叠加原理，求出全频谱的信息再通过积分累加才能得到某一时刻的场分布。如果激励信号是很窄的脉冲，就需要在很宽的频率范围内求解，显著增加计算复杂度。根据IR-UWB信号时域极窄的特性，利用时域型的射线追踪技术通过一次卷积运算即得到宽带的频域结果更为有效[4]。在已有的研究基础上[5-7]，建立了完整的适用于穿墙计算的时域射线追踪方法(TD-Ray)。综上所述，FDTD方法便于分析有限大小的复杂损耗结构，对电大尺寸的目标计算存在消耗内存大、时间长等困难。TD-Ray技术则特别适合计算电大尺寸的规则结构，但对复杂损耗结构尤其是带有曲面结构的电磁建模存在困难。

根据上述问题，笔者提出了基于TD-Ray和FDTD的混合计算方法，充分利用IR-UWB特点，通过逆拉氏变换将传统的Ray-tracing变换到时域，并在电小结构附近用FDTD方法计算。混合方法保持了时域数值计算方法的优点，可以有效预测IR-UWB信号穿墙传播特性，并对墙后存在的不规则复杂几何结构的电小尺寸目标的电磁散射分析进行快速建模，避免了TD-Ray方法在模拟电小尺寸结构时精度不高的缺点，提高了FDTD方法的计算效率。基于穿墙人体目标平均雷达散射截面(RCS)的计算结果表明，该混合方法与FDTD方法和实验测量结果较为吻合，从而验证了混合计算方法对穿墙人体散射建模的正确性。

1 时域射线法与FDTD混合的计算模型

在UWB信号穿墙传播过程中，入射信号会产生空间扩散，墙面和地面引起的反射及透射，穿透墙体内部的损耗，门窗及障碍物的绕射及房间内部小尺寸复杂结构体的散射等物理现象。混合计算模型的基本思想是对大范围穿墙区域以时域射线追踪来实现传播建模，在不规则复杂几何结构处用FDTD方法进行电磁散射建模。在大范围穿墙区域内，对点源的每条初始射线进行追踪，记录IR-UWB信号的传播路径，按照每一条路径遇到的电磁传播现象(如反射、透射、绕射等)卷积相应的时域传播模型(系数)，可以直接从时域构建出某一极化方式下的接收波形。当给定入射波形式E0(t)时，第i条路径的接收信号可表示为

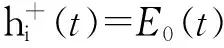
(1)

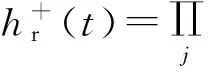
在房间内存在不规则复杂结构(特别是带有复杂曲面结构)的地方放置一个虚拟框[3]，根据时域射线追踪算法获得入射至虚拟框上的射线，记录它们的交点坐标，射线方向及电场值，然后以它作为FDTD方法的激励源。如图1所示，FDTD方法计算的区域被矩形框ABCD圈出来，矩形框的四条边即为混合方法的分界线。为了降低激励源产生的寄生波，将FDTD计算区域向矩形框ABCD外扩展一些。图1中A′B′C′D′区域表示散射场区，矩形框ABCD内部为总场区，它们的关系如式(2)(3)所示

Etot=Escat+Einc

(2)

Htot=Hscat+Hinc

(3)

下标tot，scat以及inc分别表示总场，散射场及入射场。在散射场区域，只计算散射场分量，这意味着入射波不计入该区域。

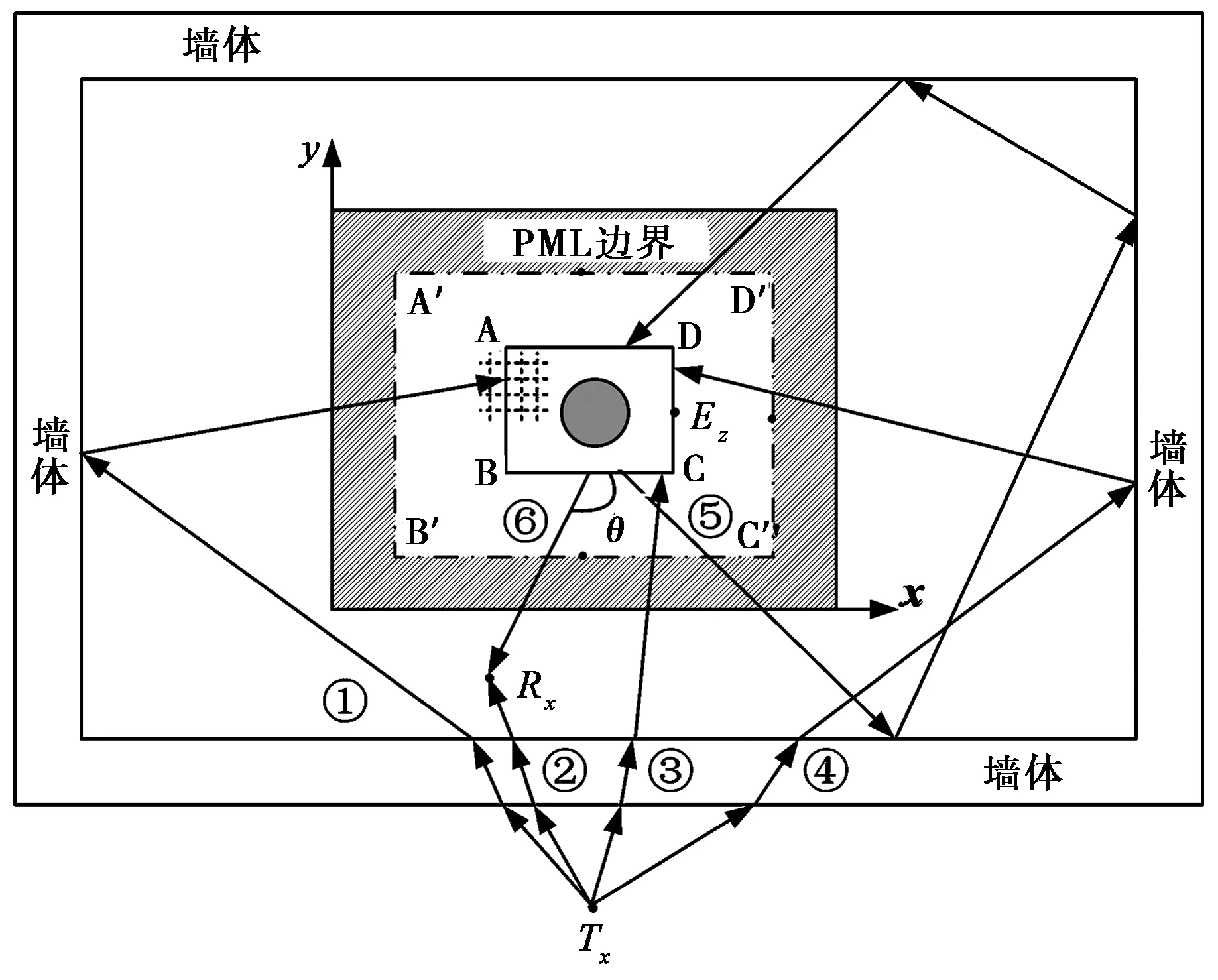
图1 混合计算方法示意图

在追踪过程中，射线遇到分界线后就被存储下来作为FDTD的激励(图1中①②③④四条射线)。经FDTD计算后波又回到分界线上(射线⑤和射线⑥)，再利用射线法将其发射出去并追踪。部分射线在房间内多次反射后又回到分界线上(射线⑤)，同理继续由FDTD追踪，直到计算时间结束或者射线能量小于一定门限即停止计算。逐一记录被接收点接收到的场强，按时间叠加后即可得到接收波形。混合方法的接收波形由IR-UWB信号在每条路径上传播现象的时域模型(系数)以及两种方法的衔接(耦合)方法共同决定，其中时域模型(系数)与入射角、极化方式、介质电导率、介电常数等因素有关，耦合方法则决定了虚拟框上由射线合并产生的激励源，以及在FDTD区散射后的TD-Ray方法的激励源。

2 时域模型(系数)和FDTD计算区域的处理方法

2.1 时域模型(系数)的计算

2.1.1 空间扩散因子的计算

空间扩散因子主要描述由于空间传播导致的IR-UWB信号能量扩散[4]。根据时域物理光学(TD-PO)方法可得

(4)

式中：E(r0)为参考点r0处场值；sinc=|r1-r0|；|A(sinc)|用射线束截面积比值的平方根来表示[5]

(5)

式中：A0、A1表示两个射线束横截面的面积；ρ1、ρ2为参考点到射线管截面变为零处的距离。

2.1.2 时域反射系数的计算

当IR-UWB信号遇到介质分界面会发生反射，根据几何光学法，信号的反射场可表示为[4-5]

(6)

式中，τr=t-di/c-dr/c、Ai(di)、Ar(dr)分别代表入射点到反射点、反射点到观测点的空间扩散因子，同样可以由式(5)得到。‘+’代表时间t的上半平面部分。

设分界面处的两种媒质的介电常数分别为ε1和ε2，磁导率分别为μ1和μ2，介质Ⅰ为空气，介质Ⅱ为有损介质如墙体等，E0代表入射波。

有损介质的复介电常数为ε=ε0(εr+σg/jω)，式中σg=120πσc.由空气入射到墙体时域反射系数r1(τr)为[4]

n·In(aτr)]

(7)

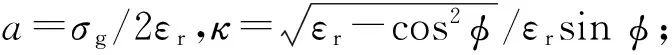
n·In(aτr)], +,hp;-,vp;

(8)

如果在传播过程中存在M次反射，则可以用

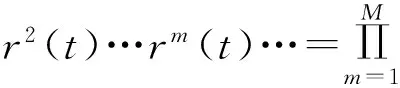
rm+(t)都可以由式(7)和(8)计算得到。

2.1.3 时域透射系数的计算

IR-UWB信号在传播过程中遇到障碍物发生反射的同时还会发生透射，透射场可以表示为

(9)

其中，τt=t-di/c-dt/c.由tvp,hp(τ)=δ(τ)+rvp,hp(τ)以及式(7)和(8)，可以得到由空气入射到介质时的时域透射系数t1(τ)，t2(τ).

2.1.4 介质内部时域传输系数的计算

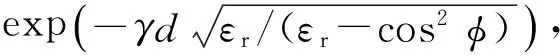
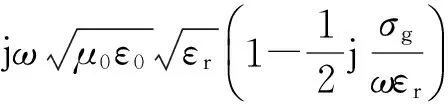
(10)

则

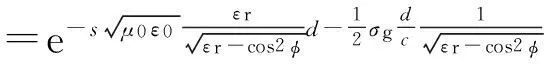
(11)

对上式做单边拉氏逆变换得

(12)

式(12)与文献[5]中的结果对照，可以说明这种近似的合理性。

2.1.5 时域绕射系数的计算

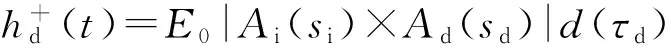
dhp,vp(t)=d1(t)+d2(t)+

rhp,vp(t)*(d3(t)+d4(t))

(13)

式中

当入射波为球面波时，L=sin2β0·ss′/(s+s′)，其中s′与s分别是绕射点到接收机与发送机的距离，β0为入射波与障碍物棱的立体角，一般为90°.

2.2 混合方法中FDTD计算区域的处理方法

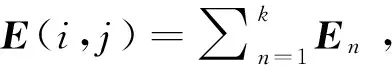
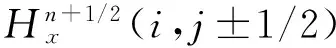
(14)

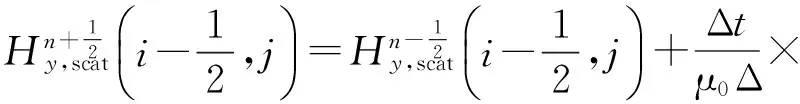
(15)

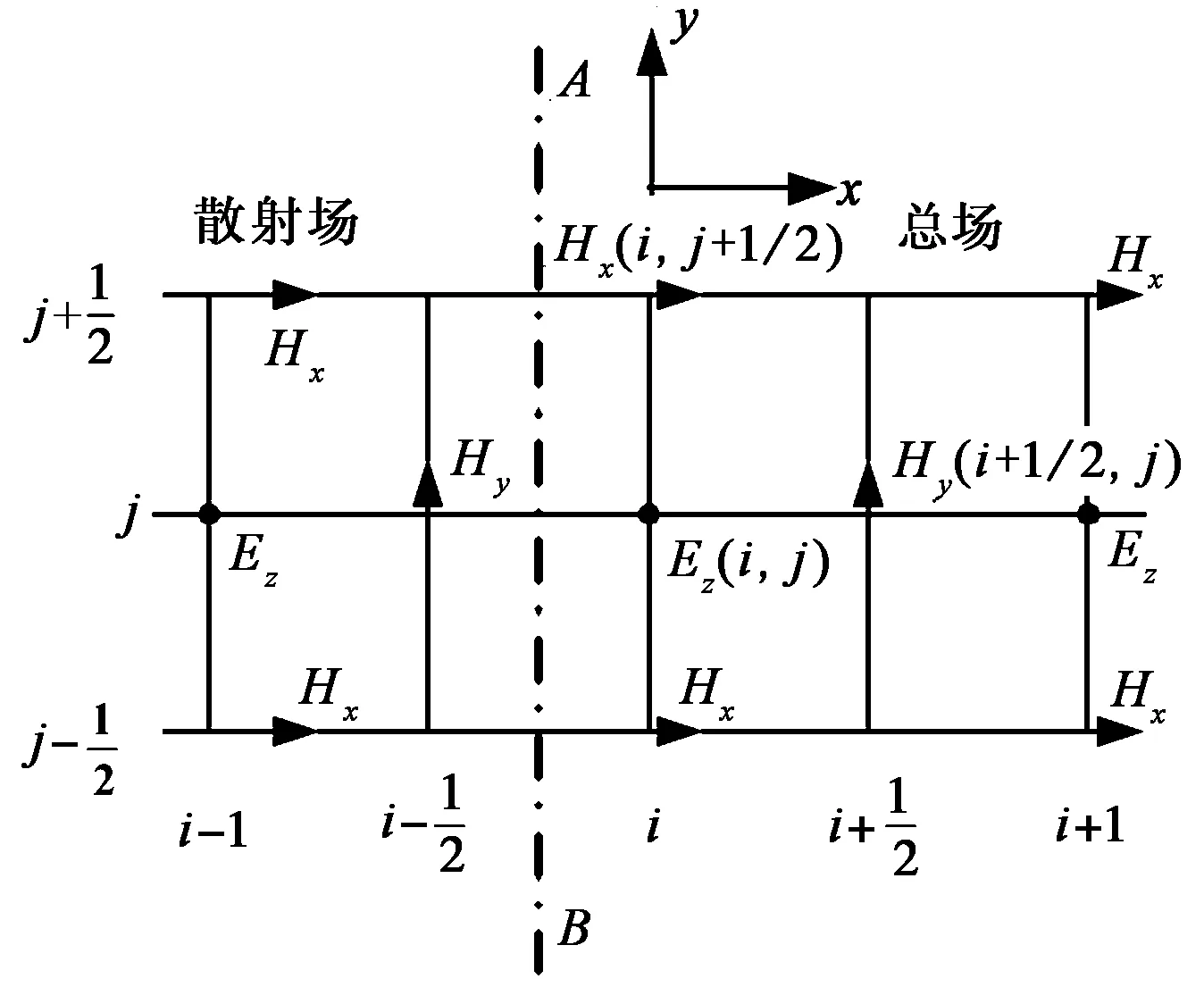
图2 总场边界附近的元胞

在FDTD计算结束以后，BC接收到由物体散射的回波，将FDTD计算的场值作为TD-Ray的源继续追踪。以图1中BC为例，将BC划分成P段，每一小段由l个网格组成，按照远场条件有l≤λmin/2[10]。根据FDTD时域近远场变换原理[11]得到第n个射线管的二次源为

(16)

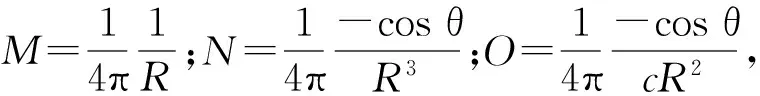
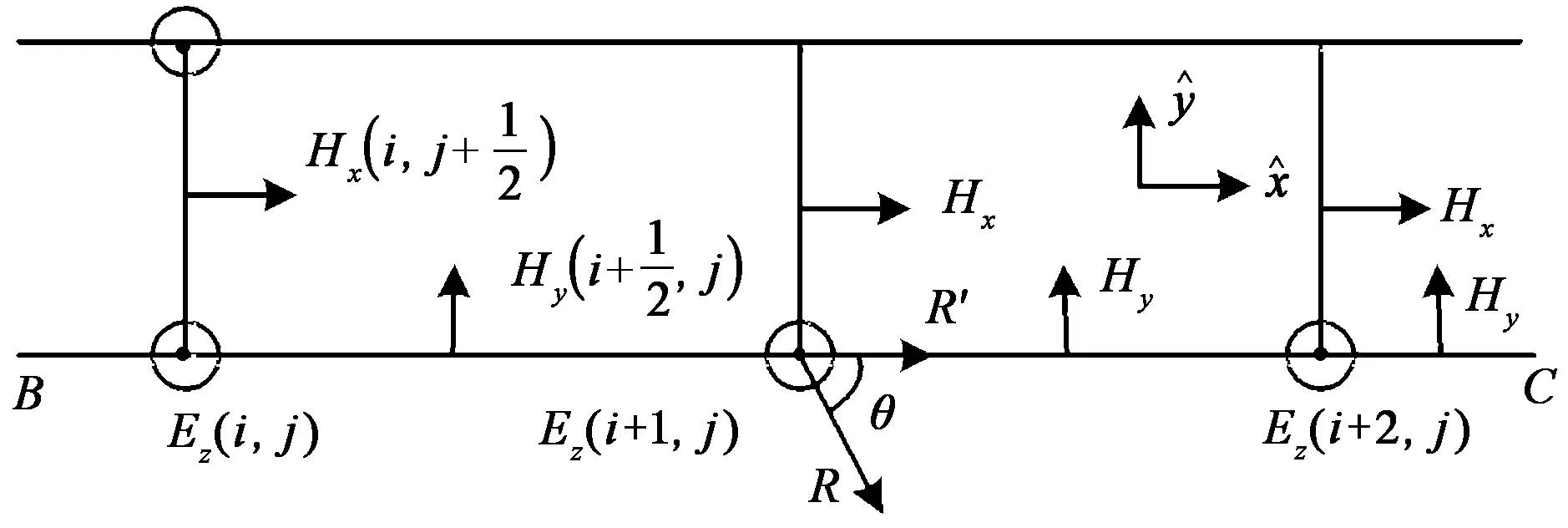
图3 FDTD方法与TD-Ray方法接口处的耦合方法

3 仿真结果分析与讨论

3.1 简单模型计算结果

利用基于二维FDTD与TD-Ray的混合方法(Hybrid method)计算墙后存在半径较小金属目标时的电磁散射回波，并与FDTD方法及TD-Ray方法比较。然后，利用三维FDTD方法及混合方法进行穿墙人体平均RCS的计算，并与实验数据进行比较。

计算场景如图4所示，墙体介电常数为εr=6，σ=0.01，墙厚24 cm，金属圆柱半径为10 cm，发射点和接收点的位置分别如图4中黑点标识所示。墙体坐标如图中所示，房间长为9 m，宽为6 m， 金属圆柱尺寸相对于房间尺寸非常小，虚线框所包围的区域为FDTD计算区域，框外为TD-Ray计算区域。

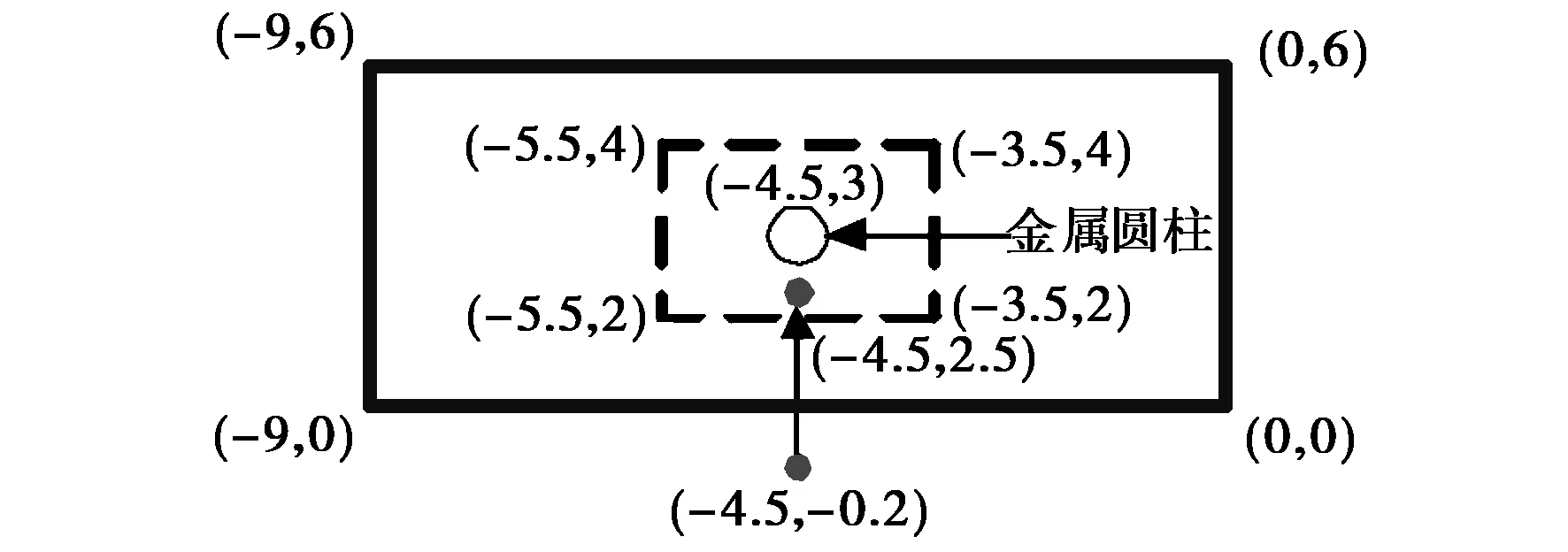
如果射线弹到虚线框上记录射线到达点坐标，时间、场值。图4 计算实例：9 m×6 m房间内有一金属圆柱，虚框标识处为两种算法的分界线

采用高斯二次微分脉冲作为发射源，如式(17)所示

(17)

其中，t0=1.596 ns，τ=532 ps，-20 dB频谱宽度为1～2 GHz.图5(见1061页)给出了分别利用混合方法、TD-Ray和FDTD方法计算图4场景得到的接收波形细节对比结果。以FDTD方法得到的接收波形作为参考，从图5中①②的细节对比中可以看出，混合方法结果优于TD-Ray方法，其与FDTD结果归一化距离为0.23，而TD-Ray结果归一化距离为2.01.这是由于计算场景不仅包含电大尺寸的墙体结构，还包含电小尺寸的目标结构—墙后金属圆柱。因为该金属圆柱半径非常小，在TD-Ray模型中仅能追踪到很少的目标散射射线，因此得到的计算结果误差较大。而混合方法在电小结构附近采用了FDTD方法进行建模，避免了这一区域射线追踪的缺点，同时又综合了两种方法的优势，因而大大改善了单一TD-Ray方法的计算精度，相比单一FDTD方法而言，计算效率也大大提高了。

表1为混合计算方法在该场景下得到的信道多径时延参数，其中超量时延(Excess Delay)和均方根时延(R.M.S)[12]的定义如式(18)和式(19)所示，将这两个参数与FDTD方法得到的参数进行比较，可以发现混合方法预测穿墙场景信道模型的准确度与FDTD方法基本一致，这证明了文章所构建的混合方法是一种可以有效建模UWB穿墙传播信道的计算方法。这对UWB系统设计和性能分析等实际工程问题是十分有意义的。表2对比了上述场景下三种计算方法所消耗的计算时间。其中，混合方法初始光线数目为100条，即射线夹角α=1.8°.

表1 多径时延参数

表2 计算时间对比

(18)

(19)

通过对某一位置处接收信号过不同门限时多径数目的统计分析，可以更定量、直观地评估计算方法的性能。图6通过改变混合方法中初始追踪射线数目得到了不同门限下的多径数目分布。

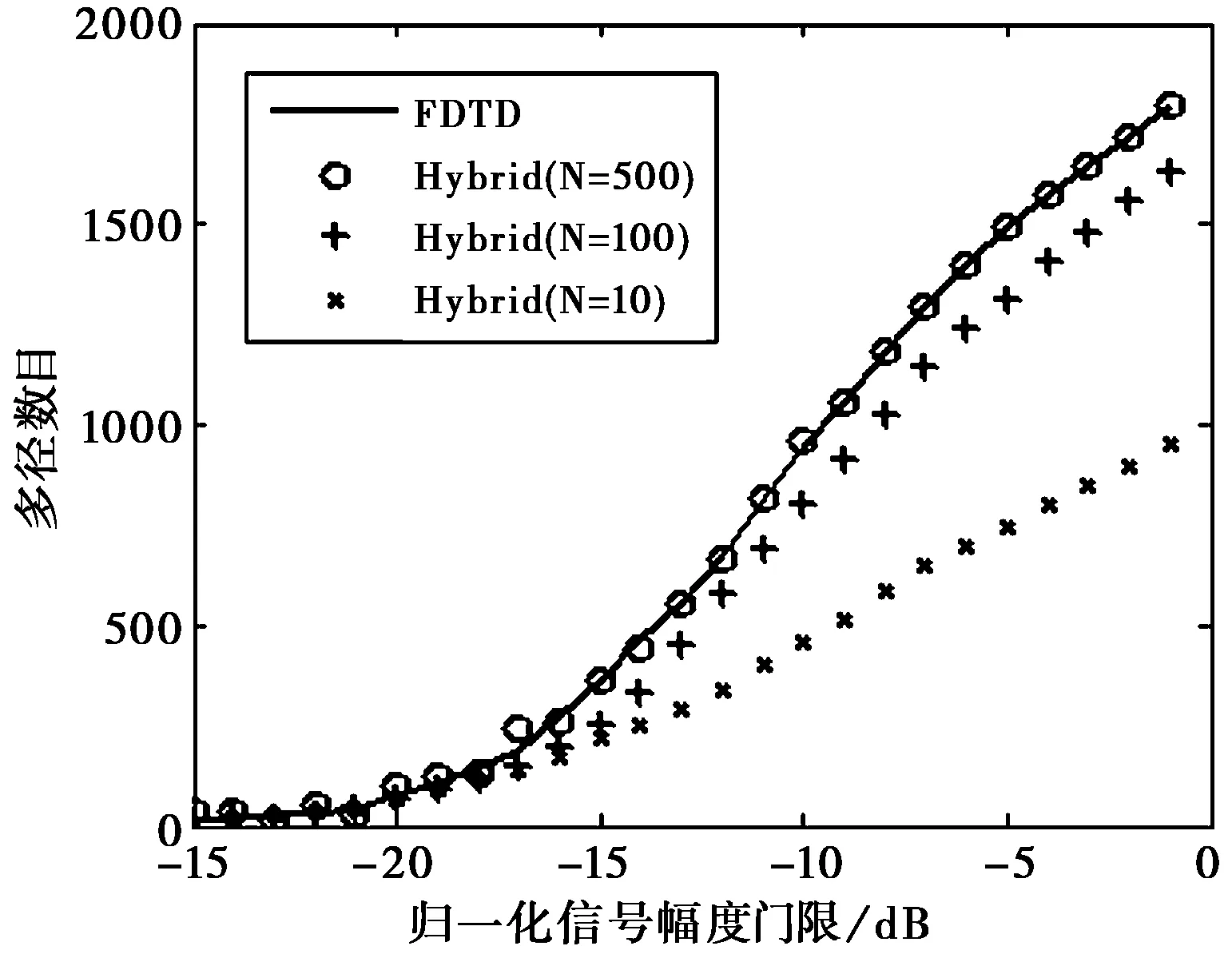
图6 不同射线数对仿真的信道多径的影响

在图中，N=100和N=500这两条曲线都与FDTD精确结果吻合得较好，这说明适当降低射线追踪数目并不影响混合方法的计算精度。利用混合方法建立超宽带信道模型时，可以根据信道环境所需要的建模精确程度，选取不同的初始射线数目。在相同模型准确度条件下，混合方法比传统方法具有更短的实现时间。

3.2 穿墙人体目标平均RCS

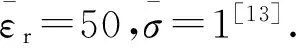
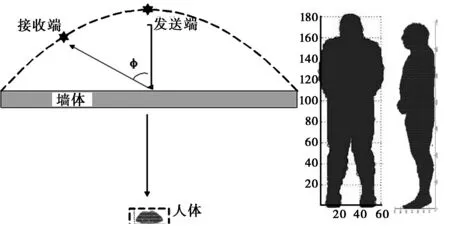
图7 (左)墙后人体平均RCS计算场景，(右)建立的人体模型，左图是按1 cm网格剖分的正视图，人体尺寸为62×17×178(元胞)，右图是按0.26 cm网格剖分侧视图，人体尺寸为238×66×700(元胞)

f=1～2GHzεrσ红砖墙(厚24cm)5.850.03

在计算过程中，混合方法初始追踪光线数目为200条， FDTD网格长度为1 cm，时间步为16.68 ps，采用8层PML吸收边界，吸收边界反射率为1×10-6.利用仿真得到的回波数据按公式(20)计算了频率范围在1～2 GHz的IR-UWB信号穿过墙体后的人体平均RCS

(20)

将FDTD和混合方法计算结果与室外穿墙人体平均RCS测量结果进行对比，如表4所示。表中实验数据由外场实验测量获得，实验方法参见文献[14]。从表4可以看到，在某些接收机位置处(如V-V极化φ=0°)，混合方法的预测结果会更接近实际结果。这并不是说混合方法比FDTD方法更准确，造成这个现象的原因有两个：第一，这种外场测量方法本身具有一定的误差，虽然在实验时已采取了多次实验求平均的方法来避免这种误差，但是也不能保证完全消除这方面的影响。第二，因为RCS所描述的是能量特征，所以就算接收波形细节不够准确，也不一定会影响其散射回波的能量计算。这从图5中的①也可以看出，尽管混合方法获得的波形细节不够丰富，但是与FDTD方法得到的回波能量差别不大，甚至有时候这种波形细节的误差还会令混合方法更接近实测。在本算例中，实测结果仅作为一个参照，通过其与理论结果对比，验证理论方法在预测人体目标RCS的有效性，而不能作为算法衡量标准，更精确的RCS测量需要在微波暗室中进行。在某些角度下，由混合方法得到的穿墙人体平均RCS与FDTD方法计算差别较大，这是由时域射线法系数如式(5)和(6)推导过程中的近似条件造成的，关于入射角度带来的时域系数误差的分析可以参见文献[4]。通过FDTD方法和混合方法的结果对比可以看出，在这种电大、电小尺寸共存的组合目标UWB电磁散射建模问题上，混合方法可以获得和FDTD一样令人满意的预测结果，是一种有效的UWB穿墙电磁散射建模方法。

表4 穿墙人体平均RCS

4 结 论

基于FDTD和TD-Ray的混合计算方法可以对IR-UWB信号的时域传播特性进行有效预测和分析。它充分考虑了IR-UWB信号特点，避免了FDTD方法中在大面积的均匀介质(如空气等)处进行密集的网格剖分，可对组合尺寸环境进行快速的时域电磁分析，大大减少了计算时间和内存消耗。

[1] 季 忠, 黎滨洪, 王豪行, 等. 用射线跟踪法对室内电波传播进行预测[J]. 电波科学学报, 1999, 14(2): 1-7.

JI Zhong, LI Binhong, WANG Haoxing, et al. Propagation Prediction in Indoor Environments Using Ray-tracing Technique[J]. Chinese Journal of Radio Science, 1999, 14(2): 1-7. (in Chinese)

[2] 潘顺康, 吕善伟, 周 沁, 等. 物理光学法在吸收体散射特性研究中的运用[J]. 电波科学学报, 2008, 23(3): 534-538.

PAN Shunkang, LV Shanwei, ZHOU Qin, et al. Scattering Analysis of Absorber by Physical Optics Method[J]. Chinese Journal of Radio Science, 2008, 23(3): 534-538. (in Chinese)

[3] WANG Ying, SAFAVI-NAEINI S. A Hybrid Technique Based on Combining Ray Tracing and FDTD Methods for Site Specific Modeling of Indoor Radio Wave Propagation[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(5): 743-754.

[4] BARNES P R, TESCHE F M. On the Direct Calculation of a Transient Plane Wave Reflected from a Finitely Conducting Half Space[J]. IEEE Transactions on Electromagnetic Compatibility, 1991, 33(2): 90-96.

[5] WANG YANG. Transmission Characteristics of Ultra-wide Band Impulse Signals[C]. Wireless Communications, Networking and Mobile Computing, 2007: 550-553.

[6] VERUTTIPONG T W. Time Domain Version of The Uniform GTD[J]. IEEE Transactions on Antennas and Propagation, 1990.

[7] YAO R, GAO G. UWB Multipath Channel Model Based On Time-domain UTD Technique[C]. IEEE Global Telecommunications Conference, 2003: 1205-1210.

[8] 黄永明, 吕英华, 徐 立, 等. 以改进的混合方法预测室外到室内的电波传播[J]. 电波科学学报, 2003, 18(4):428-432.

HUANG Yongming, LU Yinghua, XU Li, et al. Prediction of Radio Wave Propagation from Outdoor to Indoor Using an Improved Hybrid Method[J]. Chinese Journal of Radio Science, 2003, 18(4): 428-432. (in Chinese)

[9] 葛德彪, 闫玉波. 电磁波时域有限差分方法[M].西安: 西安电子科技大学出版社, 2005.

[10] WANG Ying, CHAUDHURI S K, SAFAVI-NAEINI S. An FDTD/Ray-tracing Analysis Method for Wave Penetration through Inhomogeneous Walls[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(11): 1598-1604.

[11] RAMAHI O M. Near-and Far-field Calculations in FDTD Simulations Using Kirchhoff Surface Integral Representation[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(5): 753-759.

[12] GHASSEMZADEH S S, JANA R, RICE C W, et al. Measurement and Modeling of an Ultra-Wide Bandwidth Indoor Channel[J]. IEEE Transactions on Communications, 2004, 52(10):1786-1796.

[13] DOGARU T. Computer Models of the Human Body Signature for Sensing Through the Wall Radar Applications[DB/OL]. 2003 DTIC Document. http://oai.dtic.mil/oai/oai verb=getRecord& metadataPrefix=html&identifier=ADA473937.

[14] 赵国群, 朱 峰, 刘丽娜, 等. 基于室外场RCS精确测量分析[J]，现代电子技术, 2008, 31(11): 12-14.

ZHAO Guoqun ZHU Feng LIU Lina, et al. RCS Precision Measurement Analysis Based on Room Outfield[J]. Modern Electronics Technique, 2008, 31(11): 12-14. (in Chinese)