时差定位系统的缩比实验原理分析*

姚山峰，贺 青，熊瑾煜

(盲信号处理国家重点实验室，成都610041)

无源时差定位是一种高精度的定位体制，它利用多个传感器接收来波信号的到达时间差(Time Difference of Arrival，TDOA)和辐射源位置之间存在的几何关系来对目标定位，具有高度的隐蔽性、广泛的实用性和精确的目标识别特性等优势［1－2］。目前，时差定位技术的应用领域越来越广泛，在军事、工业、气象、移动通信和无线传感器定位等领域中发挥着重要作用。近年来，国内外关于时差定位的研究很多，取得了大量成果。根据时差测量值得到的定位方程组具有非线性特点，通常需要先将其转化为线性方程组之后进行求解。文献［1］采用二重最小二乘算法给出了定位方程组的非迭代闭式解，在时差测量误差比较小时，具有最优估计性能，但随着时差测量误差的增加，该算法性能迅速下降。泰勒级数展开算法［2］是求解非线性方程的有效方法，具有精度高、鲁棒性强等特点。但是它要求迭代运算的初始值必须具有一定的准确度才能够保证比较快的收敛速度，而且算法是否收敛与初始值有关。文献［3］使用最小二乘算法估计目标初始位置，然后通过泰勒迭代算法得到目标真实值，该算法既具有泰勒级数展开算法精度高、鲁棒性强的优点，又克服了泰勒级数展开算法在某些条件下无法收敛的缺点。文献［4］对多信号交叠环境下的时差定位算法进行了研究。文献［5］指出时差定位系统的定位精度与站址误差及时差测量误差，目标与观测站之间几何位置等因素有关，文献［6－8］针对平面时差定位与三星时差定位精度问题，讨论了目标位置、观测站位置、时间测量误差和观测站站址误差对定位精度的影响。针对目标与观测站之间的几何位置对定位精度的影响，文献［9］使用加权离散搜索优化算法求解网内各观测器每一时刻的最佳观测位置，实现移动平台无源传感器网络的实时优化部署，该算法通过在最佳位置测量目标辐射源的到达时间差，完成目标运动分析，提高了对运动目标的定位跟踪精度。这些研究成果主要集中在定位求解算法、不同特性信号的时差估计算法、定位精度分析、布站优化等方面［1－10］，而对于时差定位系统性能指标的实验验证，相关研究并不多见。目前，在场地和其他条件受限的情况下，缩比实验是测试时差定位系统性能的途径之一，具有规模小、成本低、可行性高等优点，是工程实践中经常采用的一种验证办法。缩比实验技术指在满足一定条件下，将真实系统按一定缩尺比例缩小(或放大)成便于测试的模型系统，通过对模型系统的研究和测试，得到真实系统中的规律［11］。缩比实验以其可实现性强、重复性好、实验数据可靠等优点，在 RCS 测量［12］、空气动力测量［13］、射频仿真［14］等领域得到广泛的应用。

本文针对时差定位系统性能指标受场地、经费等条件所限不能进行实际场景验证的问题，对时差定位系统的缩比试验方法展开了研究，从理论上推导缩比模型与真实场景的可比性，为时差定位系统的缩比试验提供理论支持。论文首先对时差定位原理与定位精度进行分析，得出了时差定位误差的克拉美罗下界(Cramer-Rao Lower Bound，CRLB)，然后重点从几何相似性和时差测量精度相似性两个方面对缩比模型和实际模型进行了分析比较。本文的研究可为时差定位系统性能测试提供了一种可行的验证方式。

1 时差定位原理与定位精度

时差定位又称为双曲线定位，是一种重要的无源定位方法，它是通过处理三个或更多个观测站采集到信号之间的到达时间差，通过几何关系计算实现定位。对于二维平面内的目标辐射源，利用辐射源信号到达两观测站的时间差即可确定一对以两站为焦点的双曲线，通过布置三个观测站就可形成两对双曲线来产生交点，以确定辐射源的位置。若要确定三维空间内任意目标辐射源，辐射源信号到达两观测站的时间差确定了一对以两站为焦点的双曲面，则至少需要四个站形成三个单边双曲面来产生交点，以确定辐射源的位置。二维平面时差定位系统的示意图如图1所示。

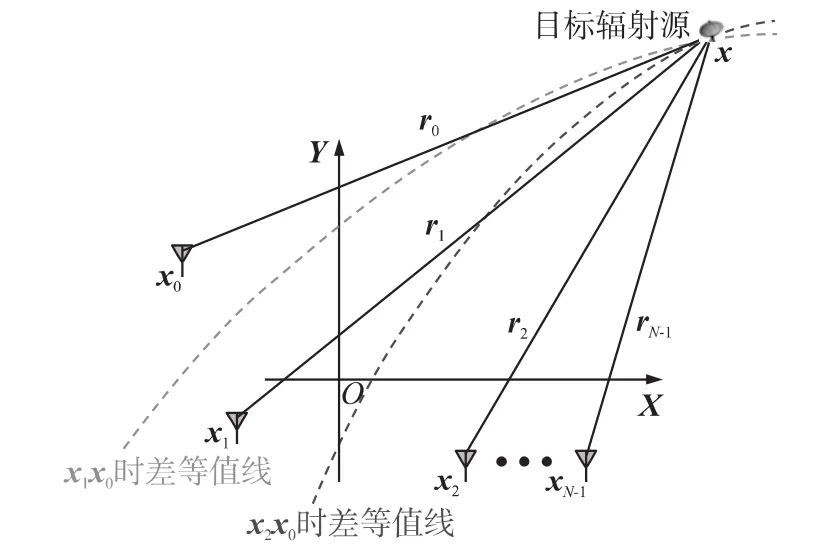
图1 时差定位原理示意图

图1中，目标辐射源位于x处，N个观测站分别位于 xi处，而 i=0，1，….N－1，目标辐射源到第 i个观测站的距离矢量为ri。选定x0为主站，其余观测站为副站，则根据目标信号到达主站与副站的时间差就可以得到N－1条单边双曲线，这N－1条单边双曲线的交点即为目标辐射源位置。根据观测站估计出的时差可以写出如下N－1个定位方程

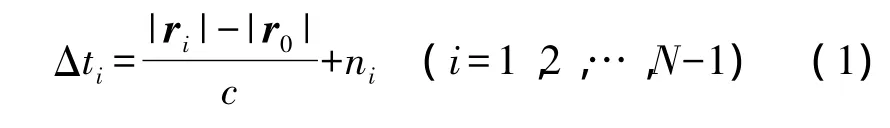
其中:ri=xi－x;r0=x0－x;c为光速;ni为时差测量噪声。

通过求解定位方程组即可实现对目标辐射源的定位，写成矩阵的形式为

其中:t为观测矢量;x为待估计矢量;n为噪声矢量;

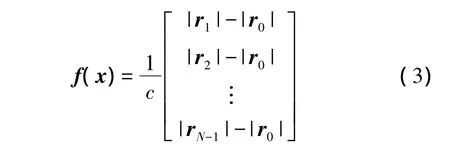
通过最小二乘即可得到x的估计^x。

根据统计信号处理理论，任意无偏估计量的估计误差方差即均方误差(MSE)都不能低于某个下界，这就是克拉美罗下界(CRLB)［15］。在高斯白噪声条件下的时差定位系统中，目标位置x的CRLB为:

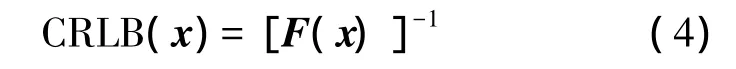
式中，F(x)为关于待估计矢量x的Fisher信息矩阵

式中，Qt表示时差测量向量的协方差矩阵，J为雅可比矩阵

于是，定位误差的CRLB为［16］

其中，tr(·)表示矩阵求迹运算。

由式(7)可以看出，定位误差的CRLB与目标位置、观测站位置以及时差测量精度有关。

在实际工程中，除了定位误差之外，还常用相对误差来衡量无源定位系统的定位精度，相对误差定义为定位误差与目标辐射源到主站的距离之间的百分比

2 缩比模型相似性分析

当受测试场地、实验条件、研究经费等因素限制，无法对时差定位系统进行实验验证时，可考虑采用缩比实验，将真实系统按一定缩尺比例缩小(或放大)成便于测试的模型系统，通过对模型系统的研究和测试，验证真实系统的性能。

对于无源时差定位系统，为了使时差定位缩比实验结果能反推出原始系统的定位性能，需要了解缩比模型与原始场景的相似关系，得到缩比模型与原始场景之间定位误差的比例关系。

2.1 几何相似分析

按照几何相似原则，将观测站与目标辐射源位置以1∶δl的比例几何等比缩小，δl称为相似比或缩放因子。图2中目标辐射源由x处缩小δl倍到x'处，N个观测站分别由xi缩放到x'i，此时目标辐射源到每个观测站的距离也缩小了δl倍。

图2 几何缩比场景示意图

此时定位方程

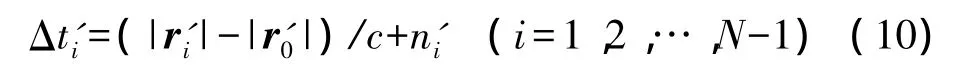
其中:r'i=x'－x'i;r'0=x'－x'0;n'i为时差测量噪声。

同理，x'的 CRLB为

式中，Qt表示时差测量向量的协方差矩阵，J'为雅可比矩阵

其中，

观察式(6)、式(14)，可得

也就是说，与原始场景相比，缩比模型条件下的雅可比矩阵并没有发生变化，这是不难理解的，

因为当满足几何相似缩比时，缩比场景中观测站与目标辐射源之间的几何结构并没有发生变化，从而缩比实验时，几何因子对CRLB的影响并不会发生变化。而通过前文对定位误差CRLB的分析可知，定位精度的CRLB除了与观测站与目标辐射源之间的几何关系有关之外，还与

时差测量精度有关，下面将继续分析时差测量精度的相似关系。

2.2 时差测量精度相似性分析

时差测量误差由相互独立的系统固有误差与时差估计算法的误差两部分组成。其中，系统固有误差包括观测站之间的时间同步误差与接收预处理系统中天线、接收机、变频器、A/D采集卡、放大模块以及传输线缆等将引入的时延差等，与目标位置与辐射信号特性无关，可通过校正算法消除;时差估计算法的误差受信号带宽、积累时间、信噪比等因素的影响，与目标位置与辐射信号特性有关。

针对矩形谱信号的时差估计误差，文献［17］指出，采用最优估计所能达到的时差估计精度为

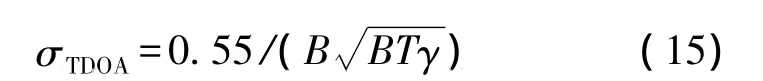
其中:B为带宽;T为时宽;γ为等效输出信噪比

可见，信号带宽、积累时间以及信噪比通过影响时差测量精度可以间接地对定位误差产生影响。带宽缩放系数δB、时宽缩放系数δT、信噪比δγ的缩放相似比与时差测量误差缩放相似比之间的关系为

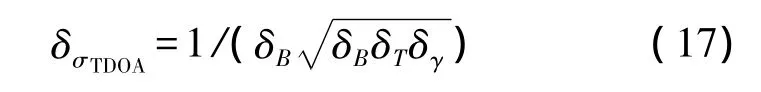
同时，信噪比由信号功率和噪声功率决定，而环境噪声与热噪声对于原始场景与缩比模型中时差定位系统的影响是一致的，当至少一路信噪比较高时，γ≈2γ1γ2/(γ1+γ2)，此时 δγ=δP/δ2l，其中，δP为发射信号功率的缩放相似比。于是

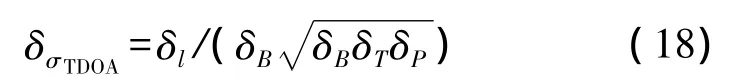
当信号带宽缩放因子为δB，积累时宽缩放因子为δT，信号发射功率缩放因子为δP时，观测站的接收功率将缩放 δP/δl，输出信噪比同比缩放 δP/δl，估计误差缩放因子为

当通过参考源等方法校正系统固有误差使其可以忽略时，缩比模型中定位误差将会减小倍，相对误差将变为原来的当目标辐射源的信号参数不发生变化，只是地理位置发生几何缩比时，δB=1，δT=1，δP=1，定位误差将会减小 δl倍，相对误差将保持不变。

当在原始场景与缩比模型中系统固有误差对时差测量精度起主要作用时，原始场景与缩比模型的时差测量误差主要由时间同步误差与系统传输时延差决定。此时，原始场景与缩比模型的时差测量精度一致，Q't=Qt，缩比后x'处定位误差的CRLB保持不变，相对误差将增大δl倍。

在实际系统中，每个观测站的时间频率基准源大多通过GPS驯服铷原子钟获得高精度的秒脉冲与基准频率，由于观测站之间相距较远，在不同的接收位置时钟频率基准源的收星条件不同，以及GPS信号在电离层与对流层的延迟不同，导致观测站之间的秒脉冲存在一定的偏差，即时间同步误差。在缩比模型中，各个观测站之间的距离相差不大，收星条件基本相同，此时的时间同步误差较小。然而，这个偏差一般是缓慢变化的，在一定时间范围内，可以认为是一个固有的时差，工程应用中常通过引入参考站的方法予以校正消除。在系统固有误差得到校正以后，影响实际系统与缩比模型定位精度的因素主要为目标位置与辐射信号参数。当缩比模型中目标辐射源信号参数与实际系统中的目标辐射源信号参数相同，即δB=1，δT=1，δP=1 时，缩比模型中的定位误差将会减小δl倍，相对误差保持不变;当缩比模型中目标辐射信号功率缩比因子为δl，带宽、时宽保持不变时，定位误差保持不变，相对误差将会减小δl倍。

3 仿真分析与实验验证

下面在前文建立的缩比模型基础上，针对不同的实验条件进行三站二维平面时差定位性能仿真分析与外场实验验证。

实验中，观测站位置信息如下表所示，时差测量精度为50 ns，几何缩比因子为10，也就是当原始场景的X轴分析范围为(－200，200)，Y轴分析范围为(－200，200)时，缩比后X 轴的等效分析范围为(－20，20)，Y 轴等效分析范围为(－20，20)，单位为 km。

表1 观测站位置

在表1的观测站布站条件下，原始场景的定位误差分布图如图3所示，其中绝对误差分布图中绝对误差等值线的单位为km，相对误差分布图中的相对误差为一无量纲的百分比系数，下文中的图5、图7与之相同。

图3 原始场景定位误差分布图

假设目标辐射源位于(100，0)处，采用Chan算法直接求解目标位置，经过200次蒙特卡洛仿真得到定位结果如图4(a)所示，定位误差曲线如图4(b)所示。

图4 原始场景定位结果统计图

可见，在表1的观测站布站条件下，当时差测量精度为50 ns时，对于(100，0)处的目标，定位误差均值为 976.8 m，相对误差为 0.98%。

几何缩比10倍，时差测量精度不变时的误差分布图如图5所示，此时由于时差测量精度不变，在相同的等效分析范围内，定位误差不变，相对误差将增大10倍，原本相对误差小于1%的区域对应的缩比等效范围内的相对误差将达到10%。通过对比图3、图5可以发现，当时差测量误差保持不变时，原场景与缩比后等效范围内的定位误差曲线相同，在原场景中的(100，0)处的定位误差约为1 km，相对误差为1%，对应于缩比模型中的(10，0)km处，缩比模型中的定位误差同样为1 km，相对误差为10%，即定位误差不变，相对误差将增大了10倍。

图5 时差测量精度不变时缩比模型的定位误差分布图

外场实验中，采用一距实验场地10 km的车载电台发射QPSK信号，选择同一方向的某广播信号作为参考源校正系统固有误差。换算到以主站为坐标原点的测站坐标系下，电台位置为(10，0)，辐射信号带宽为36 kHz，积累时间为100 ms，调整车载电台的发射功率使得接收信噪比为15 dB，此时，利用CAF算法进行时差估计的精度为50 ns，定位结果与定位误差曲线如图6所示。

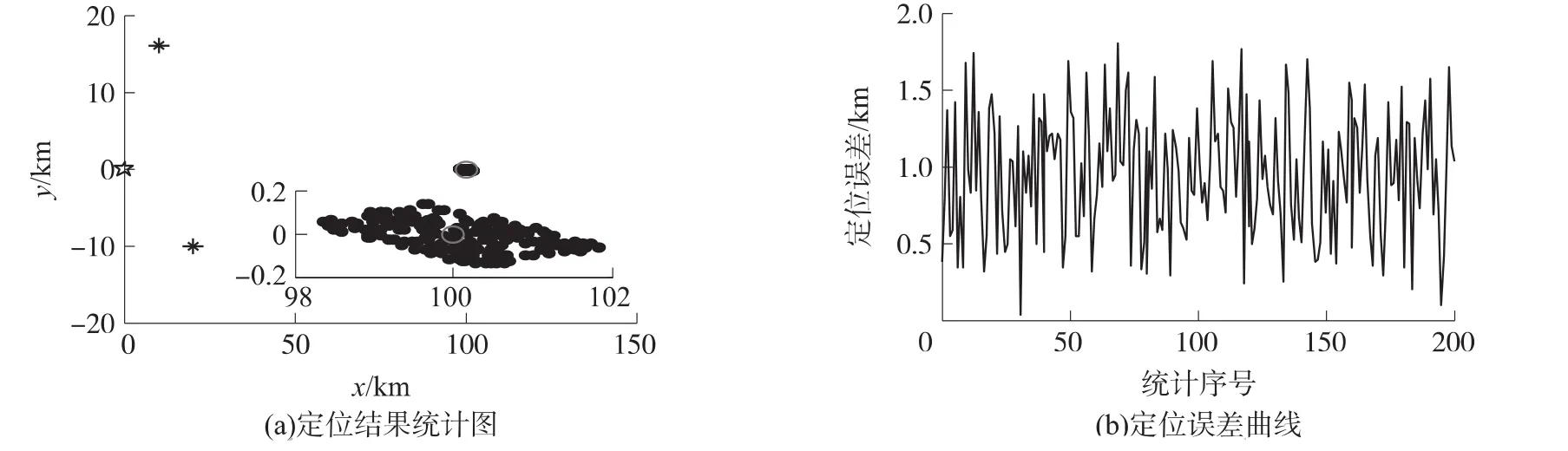
图6 缩比模型下外场实验定位结果统计图

可见，当目标辐射源由原始场景中的(100，0)处缩放10倍，变为缩比模型中的(10，0)处时，缩比模型下的定位误差均值为983.2 m，与相同仿真条件下原始场景中的定位误差相同，缩比模型下的相对定位误差为9.83%，与原始场景中的相对定位误差相比，增大了大于10倍，这与前文的结论一致。

几何缩比10倍，忽略固有误差的影响，当信号参数与发射功率保持不变时的误差分布图如图7所示。

图7 信号参数不变时的误差分布(几何缩比10倍，忽略固有误差)

此时由于信号发射功率不变，目标辐射源到观测站的距离减小了10倍，相当于 δB=1，δT=1，δP=1，δl=10，时差估计误差将减小10倍，因此，在相同的等效分析范围内绝对定位误差将减小10倍，相对定位误差与原场景保持一致。

综上，文中对原始场景以1∶10的比例几何等比缩小后，进行了2组仿真实验并利用外场实验结果与仿真分析结果进行了比对。当几何缩比10倍，时差测量精度不变时，图5所示缩比后对应分析范围内的绝对误差分布与原场景绝对误差分布情况一致，相对误差分布增大了10倍，外场实验结果与仿真分析一致。图7所示信号参数条件保持不变时的误差分布图反映了当目标辐射源发射信号不变、发射功率不变时，在对应分析范围内的目标辐射源，缩比模型下的绝对误差比原始场景的定位误差减小了10倍，相对误差保持不变。

4 结论

缩比实验是工程实践中经常采用的一种验证办法。如果想测试距主站上百公里以外区域的定位性能，可以利用缩比实验测试缩放一定倍数后缩比模型的定位性能，反推出原始场景中的定位性能。本文分析了时差定位系统原始场景与缩比模型的相似性，通过对信号带宽、积累时间、发射功率与时差测量误差、定位误差之间缩比关系的分析，得出了缩比模型下定位误差的变化规律:①当系统固有误差可以忽略，目标辐射源的信号参数不发生变化时，在几何缩比模型中，定位误差将随着几何缩比因子同比缩小，相对误差保持不变;②当时差测量精度不变时，在几何缩比模型中，绝对误差分布与原始场景一致，相对误差同比增大。实验结果证明了采取缩比实验方案的可行性，可为时差定位系统实验验证的开展提供参考依据。

［1］ Chan Y T，Ho K C.A Simple and Efficient Estimator for Hyperbolic Location［J］.IEEE Transactions on Signal Processing，1994，42(8):1905－1915.

［2］ Foy W H.Position-Location Solutions by Taylor Series Estimation［J］.IEEE Transactions on Aerospace and Electronic Systems，1976，12(3):187－194.

［3］ 熊瑾煜，王巍，朱中梁.基于泰勒级数展开的蜂窝TDOA定位算法［J］.通信学报，2004，25(4):144－150.

［4］ 罗勇江，赵国庆，斯海飞.一种多Chirp信号交叠环境下TDOA估计的新方法［J］.西安电子科技大学学报，2011，38(4):42－48.

［5］ 杨林，周一宇，孙仲康.TDOA被动定位方法及精度分析［J］.国防科技大学学报，1998，20(2):49－53.

［6］ 张正明，杨绍全，张守宏.平面时差定位精度分析［J］.西安电子科技大学学报(自然科学版)，2000，27(1):13－16.

［7］ 李文华.三星构型设计与时差定位精度研究［J］.宇航学报，2010，3:701－706.

［8］ 朱伟强，黄培康.三站时差定位系统观测站构型研究［J］.现代雷达，2010，1(1):1－6.

［9］ 顾晓婕，王新民，李文超.多站时差无源定位探测器位置优化［J］.传感技术学报，2011，24(1):93－99.

［10］ 徐耀松，李一博，付铜玲，等.有限空间液态场中基于优化EKF的双曲面水声定位方法研究［J］.传感技术学报，2011，24(11):1579－1583.

［11］ 武海军，黄风雷，陈利，等.动能弹侵彻钢筋混凝土相似性分析［J］.兵工学报，2007，28(3):276－280.

［12］ 陈晓洁，李磊，史小卫，等.半空间理想导体目标RCS缩比关系的研究［J］.电波科学学报，2006，21(6):939－943.

［13］ 陈劲松，马鸿雅，林禹.火箭发射燃气喷流缩比实验相似参数［J］.空气动力学学报，2005，23(3):307－311.

［14］ 郑星，汪连栋.缩比模型实验技术在射频仿真暗室设计中的应用［J］.电讯技术，2008，48(5):32－35.

［15］ Kay S M.Fundamentals of Statistical Signal Processing:Estimation Theory［M］.New Jersey:Prentice-Hall，1993.

［16］ 孙仲康，周一宇，何黎星.单多基地有源无源定位技术［M］.北京:国防工业出版社，1996.

［17］ Woodward P M.Probability and Information Theory with Applications to Radar［M］.New York:McGraw-Hill，1953.