舰载光电跟踪伺服系统的建模与仿真
吴晗平,胡大军,吴 晶,黄俊斌,黄 璐
(1. 武汉工程大学电气信息学院,湖北 武汉 430205;2. 海军工程大学兵器工程系,湖北 武汉 430033;3. 武汉工程大学光电子系统技术研究所,湖北 武汉 430205)
0 引 言
光电跟踪伺服系统作为舰载光电跟踪设备的重要组成部分,其设计好坏直接影响设备的性能.针对被跟踪的目标速度更快、机动性更强等情况的出现,对伺服系统响应特性、跟踪精度等性能指标也提出了更高的要求[1].在设计高性能的舰载光电跟踪伺服系统时,对系统进行建模和仿真是非常重要的环节,它可以提前发现设计中的原则性错误,验证设计是否合理.在选定光电跟踪伺服系统控制结构基础上,依据选择的关键元、部器件主要参数及初步选定的系统参数建立伺服系统的数学模型,借助MATLAB软件来仿真分析所设计的伺服系统稳态和动态特性,并确定出满足设计指标要求的并能在技术上可实现的系统参数.因此,系统建模和仿真使系统的分析和设计大为简化,可有效降低开发成本,对系统设计具有重要意义.
1 伺服系统的工作原理与结构
舰载光电跟踪伺服系统是一个位置跟随系统,具有方位和俯仰两套独立的系统.其主要接受图像处理计算机、主控计算机、陀螺仪、旋转变压器等部件的指令、状态和误差信号,然后经过数字信号处理器(Digital Signal Processor, DSP)进行综合处理,获得驱动伺服转台电机转动的控制电压来完成对转台的操作和控制,从而实现光电跟踪设备视轴的稳定和对目标的准确跟踪.
为了满足伺服系统具有快速响应特性、高跟踪精度和可靠性控制等要求,控制系统一般采用多闭环的串级复合控制结构,由电流环、速率环和位置环三个回路组成[2-4].运动载体上的伺服系统要受到舰船摇摆的影响,尤其是在恶劣的气象条件下,船体的摇摆以及风力矩等各种因素将会使跟踪转台光轴偏离瞄准目标,同时载体在方位、俯仰方向上的角运动或振动通过摩擦耦合导致光电跟踪转台的抖动,进而引起光电成像传感器准线视轴的抖动.为解决这个难题,在速率环结构上通常采用双速率环,以直流测速机为电机转速测量反馈构成模拟速率内环,利用陀螺的“空间测速机”功能组成数字稳定外环,将速率稳定环应有的抗摩擦干扰功能和隔离舰船扰动功能分开实现.具有四个回路的舰载光电跟踪伺服系统控制结构框图如图1所示.

图1 伺服系统控制结构框图Fig.1 Block diagram of servo system control
图1中,ω为电机输出的角速率,ωf为摩擦干扰力矩折算到电机轴上的角速率,ωs为舰船扰动引起的转台角速率,ωL为转台角速率,s为拉普拉斯变换复变量.
2 伺服系统主要部件的数学模型
2.1 直流力矩电机数学模型
为了分析研究的方便,直流力矩电机电枢回路的等效电路图如图2所示.
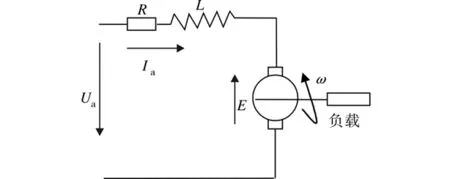
图2 直流力矩电机的等效电路Fig.2 Equivalent circuit of the direct-current torque motor
由基尔霍夫电压定律和转矩平衡方程可将直流电动机的动态特性描述为:
(1)
式中,Ua为 电枢电压;Ia为 电枢电流;R为电枢电路总电阻;L为电枢电路总电感;E为感应电动势;KB为感应电动势常数;ω为电动机转动角速度;Tem为电动机电磁转矩;J为折算到直流力矩电机轴上的转动惯量;Td为负载转矩;KT为电动机转矩系数.
设初始条件为零,将方程组式(1)拉氏变换(其中s为复变量)后可得:
(2)
消去中间变量E(s),可以得到电机的电枢回路模型:
(3)
消去中间变量Tem(s),可以得到控制电流与输出转速之间的模型:
(4)
由式(3)和式(4)推导可得电机模型方框图,如图3所示.
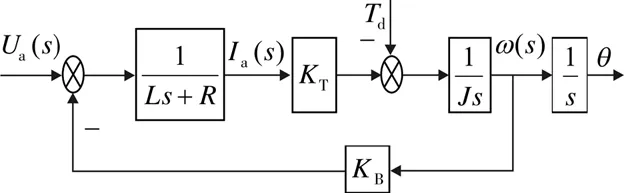
图3 电机模型方框图Fig.3 Block diagram of motor model
当力矩为零时,系统以电枢电压Ua(s)为输入变量、电动机角速度ω(s)为输出变量,直流力矩电机的传递函数为:
(5)
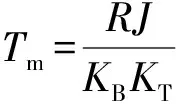
(6)
根据所选某型电机的参数可知: 电动势常数KB=4.41V/(rad/s),电动机转矩系数KT=0.245(kg·m)/A,电气时间常数Te=0.005 s,机电时间常数Tm=13 s,将以上参数代入式(6)可得方位力矩电机加负载的传递函数为:
2.2 脉宽调制功率放大器模型[5]
脉宽调制(Pulse Width Modulation ,以下简称:PWM)放大器可以看作是一个滞后的放大环节.由其工作原理可知,当控制电路的输出电压U改变时,PWM功率放大器的输出电压并没有立即改变,而是需要等到下一个周期才改变,其传递函数可以写成:GPWM(s)=KPWMe-TPWMS.当开关频率比较高,即TPWM较小,并且系统截止频率满足ωc≤1/(3TPWM)时,滞后环节可近似为一阶惯性环节,传递函数可以简化为:
(7)
式中KPWM为脉宽调制器和PWM变换器放大系数;TPWM为开关周期.
工程实际中,由于TPWM较小,数量级一般为10-4秒,可忽略不计,因此可以把它作为比例环节:
Ud=KPWMU.
(8)
本系统中控制信号提供给PWM功率放大器的电压最大值为10 V,而PWM功率放大器要输出最高值为60 V的电压提供给直流力矩电机,所以KPWM=6.
2.3 系统中测速电机、测角装置的数学模型
测速电机的响应都可以认为是瞬时的,因此它的放大系数也就是它的传递函数,即:
(9)
所选择模型测速机的参数Kv=0.3 V/(r/min)=2.867 V/(rad/s)
跟踪式旋变/数字变换器(Resolver/Digital,R/D)模块的转换速度非常快(一般都是微秒级),因而其响应也可以认为是瞬时的,其比例系数为1,旋转变压器的传递函数KB=1.
2.4 压电速率陀螺数学模型
系统采用压电速率陀螺,在平衡作用于稳定转台上的干扰力矩过程中,陀螺力矩不起作用,它只起角速度测量敏感元件的作用,消除干扰力矩作用是全部通过直流力矩电机来实现的.压电速率陀螺将扰动力矩成正比的转换成电压信号.因此,可以将其看成一个比例环节:
Gg(s)=kg,
(10)
比例系数kg由前级放大电路系数k和陀螺比例因子共同决定,由某厂提供的技术资料可知,
kg=k×0.098=0.1 (V/°/s).
2.5 电流反馈环节数学模型
电流环中使用精度很高的电阻对电流采样,由于脉宽调制型功率放大器输出的电压信号是高频脉冲,所以电枢电流Ia也含有高频分量,可采用低通滤波器将其滤除.本系统采用模拟1阶巴特沃斯滤波器,其中采样电阻的阻值取为1 Ω,低通滤波器的通带下限频率设为10 000 rad/s,所以电流反馈滤波环节的传递函数
(11)
电流反馈可认为是一个比例环节,取功率放大器的最大工作电流为12 A,则电流的反馈系数β=0.83 V/A
3 环路建模与仿真
3.1 电流环路建模仿真
作为速度内环的电流环可以使电枢电流严格跟随电压指令的变化从而准确控制电机输出的力矩,并且能够有效抑制电子噪声、反电动势等干扰量的影响,从而使测速机速度闭环的稳定精度提高.电流闭环回路由电流调节器、PWM功率放大电路、惯性环节(1/R)/(Tes+1)、电流反馈滤波环节和给定滤波环节组成,其动态结构图如图4所示.
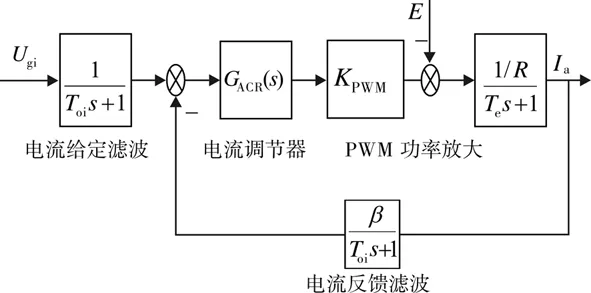
图4 电流环动态结构图Fig.4 Dynamic structure diagram of current loop
由于电流环要求超调量小并以跟随性能为主,所以将其校正为典型I型系统即可满足要求.电流环的控制对象含有两个惯性环节,通过PI型调节器可将电流环校正成典型I型系统,调节器传递函数GACR(s)为
(12)
式中,Ki为调节器比例系数;τi为调节器超前时间常数.
系统Te=0.005 s,R=4 Ω,根据2.5节可知滤波时间常数Toi=0.000 1 s.一般通过消除掉惯性较大的电机电磁特性环节来提高系统的快速性,即取电流调节器的超前时间常数τi=Te=0.005 s.将参数代入到图4,得到动态结构图(含实参)如图5所示.
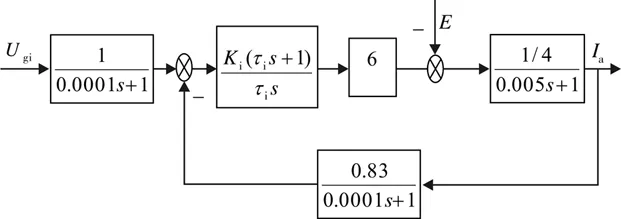
图5 电流环动态结构图(含实参)Fig.5 Dynamic structure diagram of current loop(with actual parameters)
在一般情况下,系统的电磁时间常数远小于机电时间常数,相对电流环来说,反电动势变化较慢,可以认为其基本不变,把给定的滤波和反馈滤波两个环节都等效地移到环内,经过简化和近似处理后得到电流环简化图如图6所示.
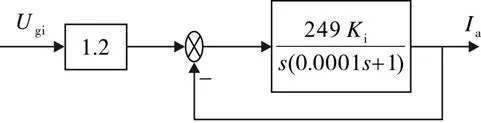
图6 电流环简化图Fig.6 Simplified diagram of current loop
按工程最佳参数来选择调节器参数[6],因此比例系数
(13)
调节器传递函数
若忽略控制器及电机输出饱和的非线性因素,对系统进行线性分析,校正后的电流环开环幅频特性、闭环频率特性和单位阶跃响应曲线分别如图7、图8及图9所示.

图7 电流环开环频率特性曲线Fig.7 Open-loop frequency characteristic curve of the current loop
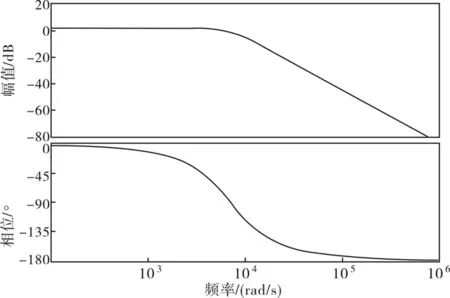
图8 电流环闭环频率特性曲线Fig.8 Closed-loop frequency characteristic curve of the current loop
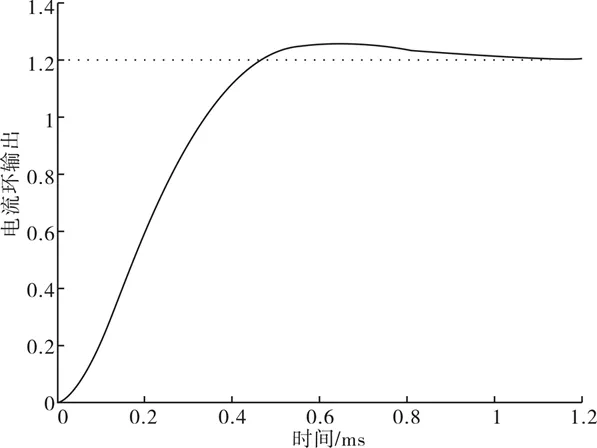
图9 电流环单位阶跃响应曲线Fig.9 Unit step response curve of the current loop
从图7可以得出,电流环的幅值裕度为98.1 dB,相位裕度为65.6 °,开环截止频率721 Hz;从图8可知,电流环闭环的截止频率ωB≈7 020 rad/s,带宽约为1 118 Hz;从图9可以得出超调量为4.4%,上升时间为0.31 ms,调整时间约为1.2 ms.
3.2 速率环建模仿真
从环路的结构看,速率环处在中间,它分别是电流环的外环和位置环的内环.在光电跟踪伺服系统中,速率环对消除摩擦力矩干扰、位置伺服精度以及低速平稳性有着显著的影响.因此,速率环设计是否合理是整个伺服系统设计的关键.
在速率环设计过程中,将校正后的电流环等效成一阶惯性环节,它与系统前向通道中的积分环节一起构成了速率环被控对象.
由3.1节可知校正后的电流环开环传递函数
作为转速环中的一个环节,它的闭环传递函数
(14)
当速率环开环频率特性的截止频率ωcn满足近似条件
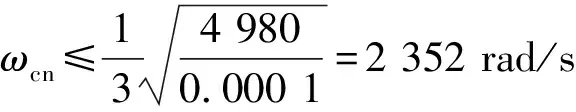
(15)
速率环调节器、电流等效环节、负载转台、速率反馈环节和给定滤波环节构成了速率环回路.设速率环调节器的传递函数为GASR(s),速率环动态结构图如图10所示.
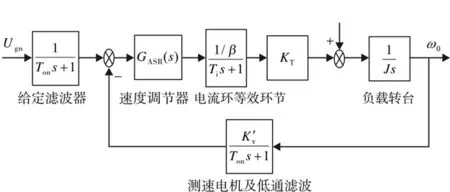
图10 速率环动态结构图Fig.10 Dynamic structure diagram of velocity loop
为使速率环在稳态时无静差和在动态时具有较好的抗扰动性能,将速率环按典型II型系统校正.根据速率环被控对象的特点,采用PI调节器来校正,调节器传递函数为:
(16)
将相关参数代入到图10,则速率环的动态结构图(含实参)如图11所示.
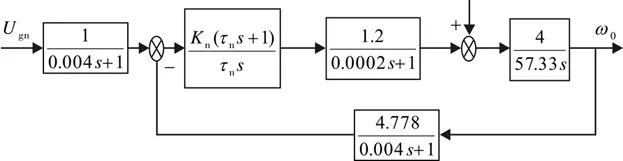
图11 速率环动态结构图(含实参)Fig.11 Dynamic structure diagram of velocity loop(with actual parameters)
与电流环类似,采用相同的简化方法,首先将给定滤波和反馈滤波环节等效地移到速率环内,然后将前向通道中的小惯性环节合并近似成一个惯性环节,其时间常数T∑n=Ton+Ti=0.004 2 s,则速率环动态结构图可以简化为图12所示.
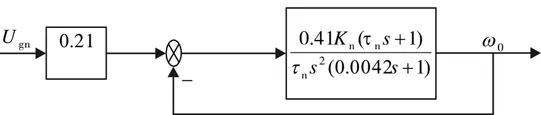
图12 速率环简化图Fig.12 Simplified diagram of velocity loop
速率环的开环传递函数
(17)
按最小谐振峰值准则选择参数[6],则有:
(18)
式中,中频宽h的大小由系统对动态性能指标的要求来决定.一般取h=5较好,此时系统动态性能最优.按式(18)可以确定速率环调节器的参数为:Kn=355.7,τn=0.021.
调节器传递函数
速率环校正后的开环幅频特性、闭环频率特性和单位阶跃响应曲线分别如图13、图14及图15所示.
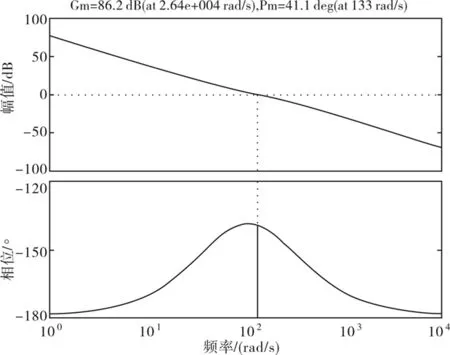
图13 速率环开环幅频特性曲线Fig.13 Open-loop frequency characteristic curve of the velocity loop
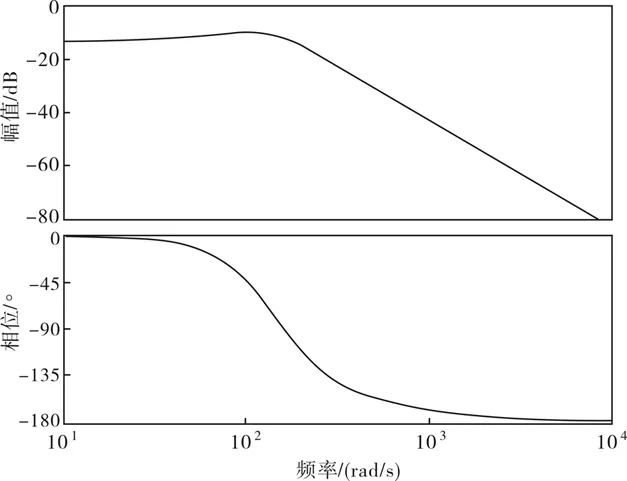
图14 速率环闭环幅频特性曲线Fig.14 Closed-loop frequency characteristic curve of the velocity loop
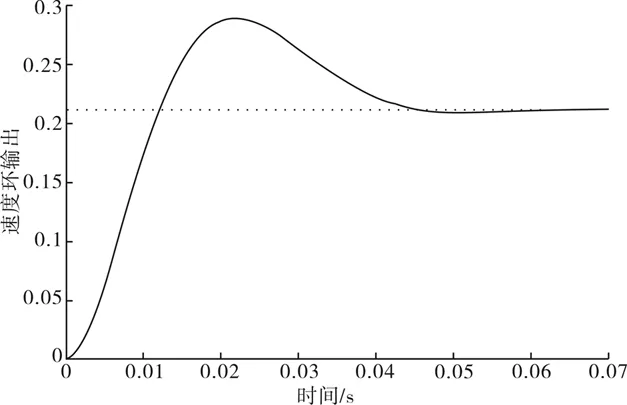
图15 速率环单位阶跃响应曲线Fig.15 Unit step response curve of the velocity loop
从图13可以得出,速率环的幅值裕度86.2 dB,相位裕度为41.1 °,开环截止频率21 Hz;从图14可知,速率环闭环的截止频率ωB≈224 rad/s,带宽约为36 Hz;从图15可以得出超调量为37.2%,调整时间约为0.04 s.
3.3 数字稳定环等效模型
数字稳定环的主要作用是隔离舰船的扰动.由安装在框架上的速率陀螺作为转台相对惯性空间角速率的敏感元件,组成一个速率闭环控制回路,通过直接驱动电机来对转台整体控制,从而保持光电传感器视轴稳定.它与以直流测速机为速度反馈所构成的模拟速度内环组成双速度环.在实际工作中,由于陀螺寿命是有限的,为满足船体在摇摆情况下的隔离度要求,才使陀螺开启,数字稳定环起作用.数字稳定环的等效模型如图16所示.稳定环调节器由数字控制器通过程序来实现.
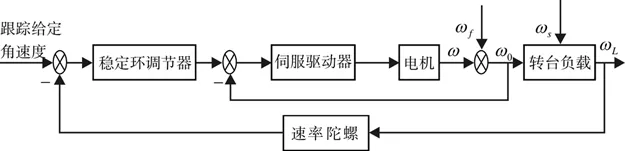
图16 数字稳定环的等效模型Fig.16 Equivalent model of the digital stable loop
3.4 位置环建模仿真
位置环是整个光电跟踪伺服系统的最外环,用来实现对转台位置的闭环控制,从而完成对目标的精确跟踪.位置调节器通常采用常规比例-积分-微分(Proportion Integration Differentiation,以下简称:PID)控制器由数字控制器通过程序来实现.根据PID控制原理及前节中建立的电流、速率环数学模型在MATLAB的Simulink环境中建立系统常规PID的位置环仿真模型如图17所示.
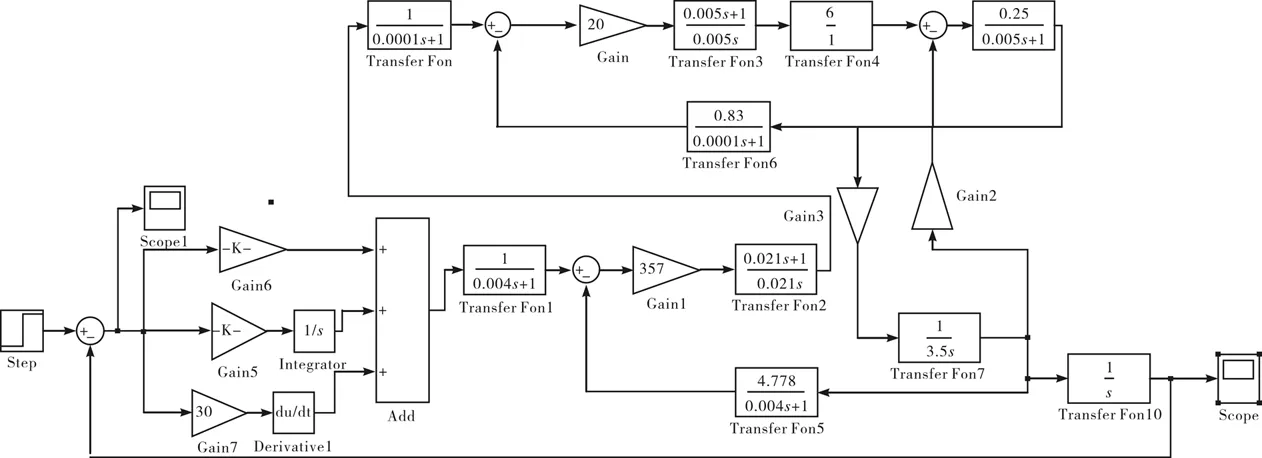
图17 系统常规PID的位置环仿真模型Fig.17 Simulation model of the conventional PID position loop
根据齐格勒-尼科尔斯法则[7]和手动试凑法并结合仿真效果整定出常规PID控制器的初始参数:Kp=435.4,Ki=3 000,Kd=10.
当系统的输入为单位阶跃信号时,其响应曲线如图18所示.
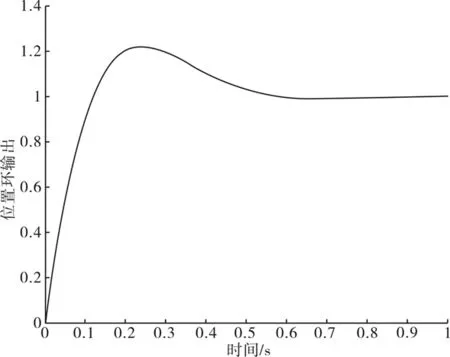
图18 系统单位阶跃响应Fig.18 Unit step response of the system
从图18可以看出常规PID控制器较好满足了无稳态误差的要求,但系统动态性能不是很理想,系统超调量较大,响应时间较长.可在此模型的基础上研究采用其他改进型的PID控制方法或其他先进控制算法来使系统的动态性能更佳.
4 结 语
结合舰载跟踪伺服系统所采用的控制结构,按照由内到外的顺序,采用分级建模、分级仿真的原则,在对伺服系统主要部件建立数学模型的基础上, 对各环路分别进行了建模,并利用MATLAB 软件对系统进行了仿真分析.通过对系统建模以及仿真分析,可以完成对伺服系统的辅助设计、调试,有效缩短系统设计周期并降低实验研究成本,可验证将先进控制算法引入到舰载光电跟踪伺服系统中的可行性.
参考文献:
[1] 段继岗.舰载跟踪雷达二自由度数字伺服系统的设计[D].西安:西安电子科技大学,2010.
[2] 吴晗平.光电系统设计基础[M] .北京:科学出版社,2010.
[3] 潘高峰,周江.船载雷达伺服系统的建模与仿真[J].电子工程师,2007,33(6):7-9,14.
[4] 权渭锋.雷达伺服系统建模与仿真[J]. 现代导航,2011(2):121-129.
[5] 徐世东.舰载稳定平台高精度伺服控制系统的设计研究[D]. 哈尔滨:哈尔滨工程大学,2008.
[6] 罗飞,郗晓田,文小玲,等.电力拖动与运动控制系统:第二版[M].北京:化学工业出版社,2007.
[7] 刘金琨.先进PID控制MATLAB仿真:第二版[M].北京:电子工业出版社,2004.

