基于机制设计理论的云计算SLA 响应时间优化*
王翠娥,顾永跟,吴小红,陶 杰
(1.杭州电子科技大学计算机应用研究所 杭州 310018;2.湖州师范学院信息与工程学院 湖州 313000)
1 引言
云计算SLA是云服务质量的重要保证[1]。针对云计算SLA中的响应时间,将在充分保障QoS[2]的前提下,最小化用户任务的完成时间定义为响应时间。云计算双市场模型中将云资源提供商和云服务提供商[3]分别作为资源代理和用户代理,在双市场中对资源需求和服务需求进行协商和匹配。在用户某项工作的预算确定以及违例赔偿明确的情况下,云服务提供商会考虑如何优化服务的响应时间,寻求一组能在最短时间内完成任务的资源组合。
机制设计是博弈规则设计的主要方法,即使博弈中的代理都是自利的,也可以通过机制设计获得一个最佳结果[4,5]。本文假设云资源提供商是自治﹑理性﹑智能的,设计的机制中,不论其他资源提供商的报价如何,真实报价是其占优策略。对于一个机制设计问题,需要考虑两个方面:一个是机制中每个代理人的目标,另一个是机制的目标[6]。在本文所设计的机制中,云服务提供商在SLA条款中预算值和违例赔偿值一定的情形下,寻求一种用户完成工作时间最短的方法。在各云资源提供商都追逐最大效用的情况下,该机制为云服务提供商寻求用户工作的最短响应时间创建了一个真实的资源成本显示环境。那么如何在理性﹑智能﹑自治的云资源提供商之间制定一种交互的协议,以促成各云资源提供商显示资源的真实成本,正是本文设计的机制要解决的问题。
2 机制设计相关概念
为了后文叙述方便,将机制设计理论中相关符号和几个重要概念列举如下。
θ:参与用户任务竞争的云资源提供商的一种类型组合,θ=θ1×…×θn。
θ-i:云资源提供商i除外的其他参与用户任务竞争的资源提供商的一种类型组合,θ-i=θ1×…×θi-1×θi+1×…×θn。
Θ:参与用户任务竞争的云资源提供商的所有类型组合,Θ=Θ1×…×Θn。
Θ-i:云资源提供商除外的其他参与用户任务竞争的资源提供商的所有类型组合,Θ-i=Θ1×…×Θi-1×Θi+1×…×Θn。
定义1 (社会选择函数在占优策略上的实现)如果一个机制M=((Si)i∈N,g(·))所导出的贝叶斯博弈 Γb有一个弱占优策略均衡,且使得那么称该机制在占优策略均衡上满足社会选择函数f(·)。
定义2 (占优策略激励兼容)如果一个直接显示机制D=((Θi)i∈N,f(·))所导出的贝叶斯博弈有一个弱占优策略均衡,其中N,那么社会选择函数f:Θ1×…×Θn→X是占优策略激励兼容的。社会选择函数激励兼容的充分必要条件为ui(f(θi,θ-i),,坌i∈N,坌θi∈Θi,坌θ-i∈Θ-i即无论其他代理人报价如何,代理人i报的真实类型θi总是其最优反应。
3 不完全信息资源成本报价模型
对于云计算任务分配,本文构建了一个不完全信息的非合作博弈模型。以博弈论的观点,假设云资源提供商是自治﹑理性﹑智能的。云资源提供商的自治性是指其策略不受云用户和其他资源提供商的影响和控制;理性是指其所选的策略是为追求自己的效用最大化;智能性是指云资源提供商知道博弈规则,并且会在选择策略时充分考虑其他资源提供商的可能行为。
在云计算中,一个用户提交的工作可以被分为多个任务,这些任务可以在云数据中心独立并行地执行。假设用户的某一项工作被划分成m个相同的任务,数据中心现有Y个云资源提供商,n为参与用户任务竞争的云资源提供商。云资源提供商i有一个任务处理速率μi,μi由资源提供商代理的服务器处理速率决定,可以视为常数,ti=1/μi表示单个任务的处理时间。此外,每个云资源提供商有一个可接受的任务数qi及处理单个任务的资源成本ci,ci为资源提供商i的私有信息,θi(ci,qi)为云资源提供商的真实类型,θ^i(c^i,qi)为云资源提供商i所报的类型。每个理性的云资源提供商都追逐各自效用的最大值,其效用记为ui(k(·),p1(·),…,pn(·),θi),价值函数vi(k(·),θi)=-ki(θ)×ci,则:
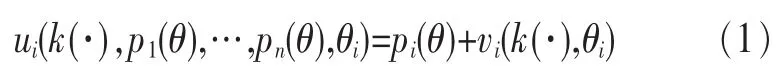
其中,k(·)和pi(θ)是机制设计的分配函数和支付函数。云服务提供商的目标是在预算值和违例赔偿值一定的情形下,为用户在SLA条款中寻找min(maxti)。
4 一种优化响应时间的机制设计
在理性参与人的假设下,Neumann和Morgenstern提出并证明了期望效用最大化理论[7]。理性的资源提供商都追求效用最大化,因此对于响应时间的优化问题,云服务提供商必须考虑各资源提供商对所提供资源报价的真实性,即希望在所有资源提供商提供真实资源成本的前提下,寻找任务响应时间最短的云资源提供商。本着这一目标,作为机制设计者的云服务提供商必须设计该机制下的支付函数和分配函数,使得参与该机制的资源提供商都愿意报出真实的资源成本。
为了更准确地分析机制设计问题,需要定义一个机制设计环境,下面介绍本文机制设计的准线性环境[8],在准线性环境下,可以找到一个激励兼容但非独裁的社会选择函数f(·)。
定义3 (机制设计的准线性环境)代理集N={1,2,…,n};可选结果集0};代理i具有类型 θi∈Θi,Θi定义为参与用户任务竞争的云资源提供商i的类型空间,类型是与决策制定有关的所有私有信息;社会选择函数f(θ)=(k(θ),p1(θ),…,pn(θ));效用函数ui(x,θ)=ui((k(·),p1(·),…,pn(·)),θi)=vi(k,θi)+pi。
其中,分配向量k(θ)=(k1(θ),k2(θ),…,kn(θ)),ki(θ)定义为云服务提供商对云资源提供商i(i=1,2,…,n)的分配函数;支付向量p(θ)=((p1(θ),p2(θ),…,pn(θ)),pi(θ)定义为云服务提供商对云资源提供商i的支付函数。
4.1 用户任务分配机制设计
4.1.1 分配函数的设计
一个有效的用户任务分配方案k(θ)=(k1(θ),k2(θ),…,kn(θ))必须满足以下条件。
·非负性:ki(·)≥0,i=1,2,…,n;
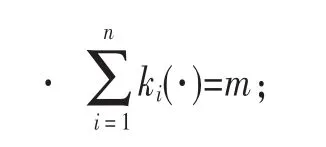
·ki(·)≤qi,i=1,2,…,n。
因此本文机制的分配函数设计如下:

其中,[i]表示所报的处理任务相关资源成本升序排列处于第i位的云资源提供商,]被定义为具有下列特点的云资源提供商:
4.1.2 支付函数的设计
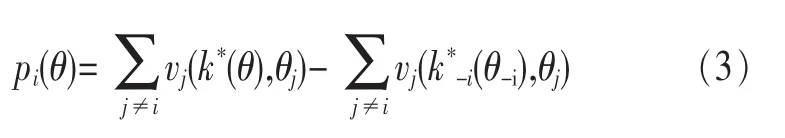
4.2 机制的性能分析
命题1 该机制满足分配有效性。
证明 首先验证该机制驱使下的云资源提供商i的占优策略(报告其真实资源成本ci),分以下两种情形。

综合上述两种情形,可知云资源提供商i在效用驱使下,令其报价i等于真实资源成本ci是其占优策略。
有了上述结论,就很容易验证本文设计的分配规则满足代理(云资源提供商)效用函数最大化,即对于被分配任务的云资源提供商,其整体资源成本是最小的。
已知价值函数vi(k(·),θi)=-ki(θ)×ci,在上述分析的基础上可将其记为vi(k(·),θi)=ki(θ)×i,将其代入k*(θ)证毕。
命题2 该机制满足弱预算均衡性。
命题3 该机制满足个体理性。
个体理性也被称作自愿参与性,社会选择函数的个体理性暗含如果一个机制实现了该社会选择函数,则参与该机制的每个代理都将有非负的效用,一般假设不参与机制时的效用i(θi)=0,即 ui(f(θi,θ-i),θi)≥i(θi),∀(θi,θ-i)∈Θ。
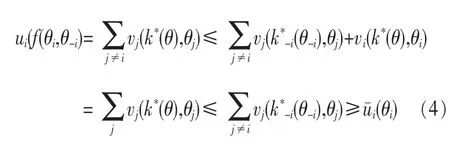
如果云资源提供商i在该机制下竞标到了任务,则完成用户任务的总成本降低,因此在i参与的情况下它的效用ui(f(θ),θi)>0;如果云资源提供商 i没有竞标到任务或者自动退出该机制,那么
由以上分析可知,云资源提供商参与该机制的效用总是不小于退出该机制的效用,具备自愿参与该机制的意向,于是该机制的个体理性得证。
命题4 该机制是占优策略激励兼容的。
下面采用反证法加强验证结论的正确性。如果一个机制是占优策略激励兼容的,那么定有下式成立:

如果本文设计的机制不是占优策略激励兼容的,那么至少存在一个代理i使得式(5)不成立,即对于代理i,云资源提供商效用函数该机制的支付函数与 θi无关,于是可以得到下式:

5 预算约束下响应时间最短的资源提供商最优组合算法
在各资源提供商真实显示资源成本的前提下,本节提出了一种预算约束下响应时间最短的资源提供商最优组合算法,描述如下:
·各云资源提供商对用户提交的工作标示出任务的处理时间和可处理的任务数,记为(ti,qi);
·云服务提供商接收云资源提供商所报的信息(ti,qi);
·云服务提供商对云资源提供商所报信息的任务处理时间ti进行升序排列;
·按任务处理时间ti的升序,从第[1]个云资源提供商到第]个云资源提供商依次选出m个任务数,满足并把相应的资源提供商添加进列表L,同时令
·e>E时,从列表中移除最大 (或剩余信息中最大)ti的相关信息;继续寻找第个云资源提供商,并添加进列表L,最后选出列表中的资源提供商。这组云资源提供商正是满足预算约束下任务响应时间最短的最优组合。
6 结束语
本文提出了一种基于机制设计理论的云计算SLA响应时间优化方案,设计了一种DSIC机制。假设云资源提供商是自治﹑理性﹑智能的,那么在这个机制中不论其他资源提供商的报价如何,真实报价是其占优策略。该机制能够保证各云资源提供商显示真实的资源成本,因此为云用户寻找到一组满足用户预算约束下响应时间最短的资源提供商是可能的,这也是本文机制设计的目标。本文的云资源报价机制为云计算SLA的设计提供了一个有利环境,在资源成本真实显示的环境下云服务提供商能优化用户服务需求的响应时间,同时在一定程度上提升了用户对云资源提供商的信任度。后续笔者将在双市场云模型中对云计算SLA中的其他参数的优化(如服务花费、违例赔偿等机制)设计问题作进一步探讨。此外,对于参与人多维私有类型信息的情况,如何设计既有较低计算复杂性又有激励兼容性的机制也有待进一步研究。
1 Armbrust M,Fox A,Grith R,et al.Above the Clouds:Aberkeley View of Cloud Computing.Technical Report UCB/EECS-2009-28,EECS Department,University of California,Berkeley,2009
2 Buyya R,Yeo C S,Venugopal S,et al.Cloud computing and emerging IT platforms:vision,hype,and reality for delivering computing asthe 5th utility.Future Generation Computer Systems,Elsevier Science,2009,25(6):599~616
3 Yonggen Gu,XiaohongWu,Jie Tao.Building an open cloud dual-market for cloud computing service.Proceedings of the 2nd International Symposium on ComputerNetwork and Multimedia Technology (CNMT’10),IEEE,2010:691~694
4 Nisan N,Ronen A.Algorithmic mechanism design.Games and Economic Behavior,2001,35(1):166~196
5 Nisan N,Roughgarden T,Tardos E,et al.Algorithmic Game Theory.Cambridge University Press,New York,2007
6 Garg D,Narahari Y,Gujar S.Foundations of mechanism design:a tutorial-part 1:key concepts and classical results.Sadhana—Indian Academy Proceedings in Engineering Sciences,2008,33(2):83~130
7 Neumann J V,Morgenstern O.Theory of Games and Economic Behavior.Princeton University Press,1944
8 Narahari Y,Garg D,Narayanam R,et al.Game Theoretic Problems in NetworkEconomicsandMechanismDesignSolutions.Springer,2009

