线性自适应小波理论的齿轮箱故障诊断方法

陈汉新, 张 琰, 刘 岑

(武汉工程大学机电工程学院，湖北 武汉 430074)

0 引 言

齿轮箱振动信号的分析[1]是现代故障诊断技术的主要组成部分.为了能准确估计机器的剩余使用寿命，进而进行行之有效的保养和维护，必须检测出故障的早期类型以及其发展趋势.齿轮箱振动图谱中最重要的部分便是由啮合频率以及其谐波和调制现象所带来的边频带这几部分构成.故障类型不同，带来的边频的数量和振幅也不尽相同.边频带是均匀地分布在中心频率周围的频率成分.中心频率也叫载波频率，即齿轮的啮合频率.齿轮故障可以只在一个齿轮上产生，一般叫做裂纹，也可以在多个齿轮上产生，便叫剥落，在这些故障齿轮啮合的过程中便产生了调制现象.最终，啮合频率以及其谐波产生了一系列边频并分布在整个范围内，且间隔的数值为转频的大小[2].

近几年针对齿轮的故障涌现出许多有效的故障诊断方法.文献[3]通过Morlet小波对振动信号进行特征提取，继而对齿轮的不同裂纹尺寸进行故障识别.文献[4]用经验模态分解(EMD)和傅立叶变换(FFT)相结合的方法能有效地对齿轮箱故障进行分类.文献[5]采用序贯概率比检验方法对多种裂纹故障进行区分.

小波变换是齿轮箱故障诊断中应用最为广泛的一种方法，因为它能展现振动信号的瞬时频率，并且用能量分布来描述频率从一个瞬时到另一个瞬时的变化趋势[6-8].希尔伯特变换在齿轮的故障诊断中是一种高效的解调方式[9].仅仅用希尔伯特变换和小波变换来从众多故障频率成分中找出特征频率是非常困难的.因此提出一种新的希尔伯特变换和自适应小波变换的线性组合来解调齿轮振动信号.结果表明了这种新方法对故障信号的诊断精度有了很大程度的提高.

1 希尔伯特变换

希尔伯特变换是实值函数在时域上的卷积，通过卷积将实值时间序列映射到另一个实值时间序列上.表示为

H[x(t)〗=1π∫∞-∞x(t)t-πdτ

(1)

其中，t表示时间，x(t)是时域信号，H[x(t)]是x(t)的希尔伯特变换.正因为希尔伯特变换是与频率无关的90°相位移动，希尔伯特变换后调制信号的非稳态频率成分不会改变.幅值和相位调制函数都可以通过希尔伯特变换提取出来.解调过程通过复数时域信号完成，这个复数时域信号也可以称为解析信号，记作A[x(t)].

A[x(t)]=x(t)+iH[x(t)]=

(2)

复数范围内的时域信号可以将实部虚部这种表示方式变换为幅值相位的表达方式：

(3)

希尔伯特变换能产生复数范围内的时间序列.这些复数的幅值就是这里要求的包络值，而且可以通过边频带估计振动信号的调制频率.

2 自适应小波变换

高斯小波是最常用的非正交复小波.标准正态自适应高斯小波函数定义如下：

ψp(t)=

(4)

φ(t)=

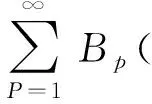
(5)

自适应高斯小波基可以通过调整时域频域的分辨率以及时频中心来得到最佳振动信号，这种方式与小波分解方式截然不同.为了提取时变振动信号的特征值，基函数ψp(t)定位在时频联合分布范围内，权值Bp反映振动信号的局部特性.参数σp、tp、fp的选取要尽可能使ψp(t)和φ(t)的值接近.参数σp主要作用是调整ψp(t)函数的带宽以确保振动信号的其他变量.自适应频谱图(ADS)可以通过以下函数获得：

φp(t)=φp-1(t)-Bp-1ψp-1(t)

(6)

(7)

其中σp∈R+,tp∈R+,fp∈[0,+∞].式(7)中的指数函数项其实就是维格纳威利分布的标准高斯函数.ADS的能量分布如下：

(8)

φ(t)的能量分布和式(8)中ADS(t,f)得到的能量分布是相同的.ADS可以看做是振动信号时频范围内的能量分布.该自适应频谱图具有非负，无交叉干扰项，高分辨率等特性.

本文的核心思路就是从信号φ(t)中提取出公式(5)中的最优参数.步骤如下：

1)运用希尔伯特变换得到振动信号的包络值.

2)将p设置为1，代入公式(6)中得到最优参数.

3)用基于粒子群算法的最优化方法去搜寻公式(7)中的优化参数(Bp,fp,tp,σp)；公式(6)的最小均方根(LMS)将做为粒子群算法(PSO)的目标函数，最终通过粒子群算法和最小均方根得到所需要的待优化参数(Bp,fp,tp,σp).公式如下：

(9)

在整个求优化参数的过程中，得到的参数集(Bp,fp,tp,σp)要使Ep值最小.

4)将所求的第一组参数值(B1,f1,t1,σ1)代入公式(5)得到原始信号的能量值φ1，再代入公式(6)得到剩余信号能量值φ2，然后通过剩余信号量φ2作为下一次循环的初始量，重复上述步骤得到下一组优化参数(B2,f2,t2,σ2)，依此类推，将得到一系列优化参数组(B1,f1,t1,σ1)×(B2,f2,t2,σ2)×(Bn,fn,tn,σn).

5)将上述优化参数序列代入公式(7)得到ADS值.

3 粒子群优化算法

粒子群优化算法[11-13](PSO)是1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart 共同提出的算法，最初只是模拟鸟类的觅食过程，通过群体合作实现最优搜索.

PSO算法从鸟类模型中归纳出用于解决优化问题的方法.在PSO中，每个优化问题的解都是搜寻空间中的一只鸟,记为“粒子”.每个粒子都有两个变量决定他们的方向和距离：位置和速度.这两个变量通过每一次的迭代进行更新，继而粒子群就追寻当前的最优粒子在空间中继续搜索.

在PSO算法的每一次迭代中，粒子通过两个“极值”来更新自己.第一个就是粒子当前搜寻到的最优解，记为个体极值pBest.另一个即整个粒子群当前搜寻到的最优解，记作全局极值gBest.

用数学模型表示如下：在一个D维的空间中，由n个粒子组成的种群，X=(X1,X2,ΛXn),其中第i个粒子的当前位置Xi=(Xi1,Xi2,ΛXiD).第i个粒子的速度为Vi=(Vi1,Vi2,ΛViD)，其个体极值为Pi=(Pi1,Pi2,ΛPiD)，种群的全局极值为Pg=(Pg1,Pg2,ΛPgD).更新公式如下：

(10)

(11)

其中，w为惯性权重；k为当前迭代次数；Vid为粒子的速度；Xid为粒子的位置；c1,c2为加速度因子；r1,r2为分布于[0,1]之间的随机数.为减少粒子搜索的工作量，通常将其位置和速度分别控制在一定的区间：[-Xmax,Xmax],[-Vmax,Vmax].将LMS作为粒子群优化算法的目标函数，即

每个粒子都需要求其目标函数，本文将目标函数也作为适应度函数，Ep的最小值即为所求适应度函数值.

4 齿轮箱实验测试系统

试验信号采集是从齿轮箱的SpectraQuest动态模拟器中得到的.在齿轮箱的垂直和水平方向各固定一个PCB352C67加速器，通过DSP20-42型信号分析仪，将采集的振动信号输入到电脑中并储存.齿轮箱的测试系统如图1所示，齿轮3和齿轮4垂直方向上的冲击力产生振动，因此选择垂直方向上的传感器更容易提取质量较好的振动信号.实验选取齿轮3或齿轮4来模拟故障.齿轮3与齿轮4之间的齿啮合相当于加载在悬臂梁上的动态载荷，梁的最大挠度由梁末端处所受的作用力、梁的长度、材料的杨氏模量以及梁的惯性力矩所决定.齿轮4的长度和惯性力矩都比齿轮3大，故本实验选用齿轮3来模拟故障.

图1 齿轮箱测试系统图Fig.1 The diagram of gearbox testing system

一般实验模拟的齿轮故障模式主要包括:齿轮裂纹，表面疲劳剥落，胶合磨损等形式.由参考文献[14]可知，齿轮裂纹是较容易测量的故障模式，所以本实验中选取裂纹来模拟齿轮的故障模式.

为了了解裂纹深度和宽度同时变化对振动信号的影响，本实验裂纹的深度和宽度均不采用固定值.假设a为弦齿厚的一半，b为齿面宽度.选取一个正常齿轮F1和三个故障齿轮F2、F3、F4进行实验，齿轮的4种模式如表1所示.

表1 四种齿轮故障模式Table 1 Four gear fault modes

本实验的样本频率设为2.56×1 024 Hz.采样点数设为2 048.齿轮箱的转速设为1 000 r/min，最大力矩载荷为41.42 N·m.齿轮的转速和特征频率是由发动机的转速和传动比决定的.转速、特征频率和力矩的总结如表2所示.表2中，f1表示轴1和齿轮1之间的转动频率；f2表示轴2和齿轮2、齿轮3之间的转动频率；f3表示轴3和齿轮4之间的转动频率；f12表示齿轮1和齿轮2之间的啮合频率；f34表示齿轮3和齿轮4之间的啮合频率.

表2 齿轮箱的转速和频率Table 2 Rotational speeds and frequencies of the gearbox

5 结果与讨论

5.1 模拟信号

这里先用模拟信号来验证公式(4)提出的自适应方法.信号cos(2π·1 560t)+cos(2π·1 600t)在区间[0,0.5]之间被调制频率为40 Hz和80 Hz的调制信号所调制.其中80 Hz的频率在区间(0,0.099)s和区间(0.301,0.5) s分布，模拟调制频率随时间的变化过程.幅值(A)调制和相位调制同时存在于该模拟信号中.(1 560+40) Hz的频率成分在这里设置为和原始信号的其中一个频率1 600 Hz是相同的.Rand(t)代表标准正态分布的高斯白噪声.

(12)

模拟信号的样本频率为4×1 024 Hz.将本文所提出的方法用在该模拟信号上得到调制信号的40 Hz和80 Hz的频率成分.具体操作步骤如下：

首先，用希尔伯特变换得到模拟信号的包络信号.图2(a)显示了公式(12)所示信号的频谱.在1 600 Hz周围有很多边频带：1 520 Hz,1 560 Hz,1 680 Hz.该图中并未见明显的40 Hz和80 Hz频率成分出现.

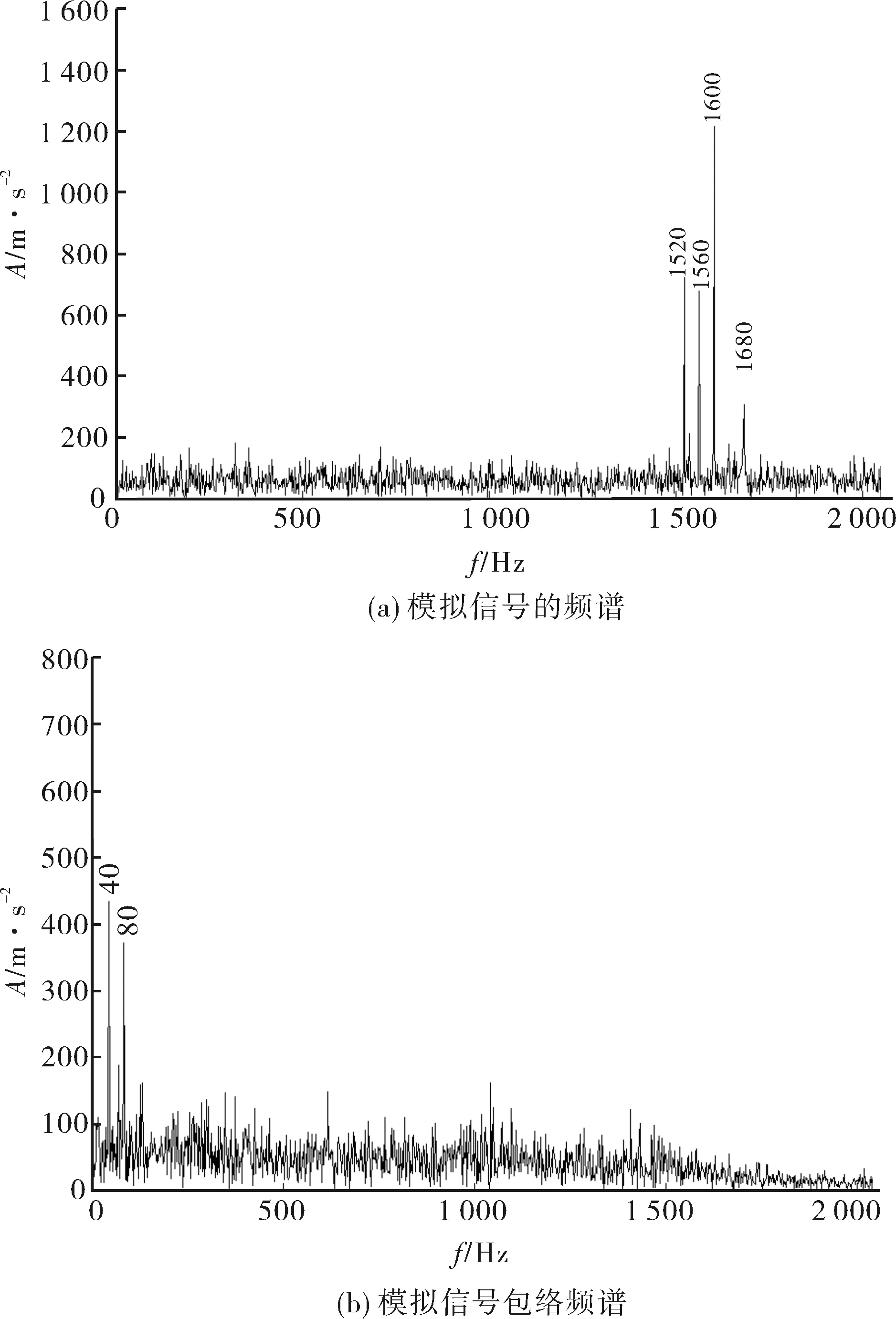
图2 模拟信号频谱和模拟信号包络频谱Fig.2 Spectrum of the simulated signal and the simulated signal envelope with hilbert transform

其次，用希尔伯特变换分析图2(a)中的包络信号.

图2(b)显示了包络信号的功率谱，其中清晰可见40 Hz和80 Hz频率成分，但是却没有将载频1 560 Hz和1 600 Hz，调制频率40 Hz和80 Hz及其倍频区分开来.

为了将40 Hz和80 Hz频率成分从希尔伯特变换得到的包络信号中解调出来，就需要使用前面提到的自适应频谱的方式.图3描述了图2(b)所示包络信号的自适应频谱，40 Hz和80 Hz的频率成分在图中清晰可见，特别是图3(b)中的80 Hz和公式(12)中显示的时间间隔一模一样.由此可见，本文提出的基于希尔伯特变换和自适应频谱方法对解决模拟信号的解调问题非常有效.

图3 模拟信号包络的自适应频谱Fig.3 The adaptive spectrogram of the simulated signal envelope from hilbert transform

5.2 实验信号

实验信号来自于SpectraQuest动态模拟器.当齿轮发生故障，比如裂纹时，齿轮箱传感器上接收到的振动信号便包含了幅值和相位的调制.啮合频率的调制问题就产生了边频带.边频带一般是轴频或是其倍频.就像在第4部分描述的那样，齿轮3上有裂纹，如图2(a)便由调制产生了边频带，或是间隔一倍轴频，或是其谐频.这里将应用上面提出的方法来得到实验信号的解调频率成分.

为了找到齿轮3产生的调制频率，先用希尔伯特变换处理实验振动信号，如图4所示.图4显示了正常和故障两种模式下的希尔伯特变换包络信号的功率谱密度.图4(a)显示了齿轮4产生的中心频率成分为7.14 Hz.齿轮1，2和齿轮3，4的啮合频率为190.48 Hz和285.71 Hz也清晰可见.图4(b)中清晰可见齿轮4产生的中心频率7.14 Hz和齿轮3、4的啮合频率为285.71 Hz.虽然在图4中可以找到7.14 Hz和285.71 Hz的频率成分，并且他们的幅值还都不相同，但齿轮3、4产生在中心频率旁的边频也同时存在.所以仅仅使用功率谱密度并不足以确定故障的存在.

图4 希尔伯特变换包络信号功率谱密度图谱Fig.4 Power desity spectrum of the hilbert transform envelope of the experimental vibration signals

这里用自适应高斯小波函数去解调轴的转频和齿轮时频范围内的啮合频率.自适应高斯小波的作用就是提取出振动信号的特征频率.图5和图6分别显示了实验振动信号的希尔伯特包络的自适应时频分布：正常状态和故障状态.图5显示的是正常状况下实验信号的自适应图谱(0～30 Hz),显示的是齿轮1和齿轮4的转频：3.97 Hz和7.14 Hz.图6显示的是故障齿轮3的转频11.9 Hz.通过比较图5和图6可以明显区分故障齿轮.通过上述讨论，当齿轮出现裂纹时，故障齿轮的转频和啮合频率都会出现.图5和图6显示的结果就证明了本文所提出的方法可以有效地提取出解调频率，如本实验的齿轮3的轴频11.9 Hz，也可以很明显地区分故障齿轮.

图5 正常状况下希尔伯特变换包络信号的自适应图谱Fig.5 The adaptive spectrogram of the experi-mental vibration signal envelope from hilbert transform under normal condition

图6 故障状况下希尔伯特变换包络信号的自适应图谱Fig.6 The adaptive spectrogram of the experi-mental vibration signal envelope from hilbert transform under faulty condtion

6 结 语

以上所提出的基于自适应小波和粒子群算法的方法能有效地提取调制频率成分和啮合频率找到故障齿轮.运用自适应小波可以提取出更多的特征信息，同时，粒子群算法优化了自适应小波的过程参数，使最终的时频分析具有较高的分辨率.本文通过模拟信号和实验信号来共同验证该方法的可靠性，结果表明，自适应小波和粒子群算法的结合比单纯的小波分析提高了时频域分辨率，即能够在高分辨率下有效的提取和区分解调频率.

致谢：本实验数据由加拿大阿尔伯塔大学机械工程学院可靠性研究实验室提供.国家自然科学基金，教育部新世纪高校杰出人才计划，湖北省教育厅对该项目提供了支持.

参考文献：

[1] 安妮, 徐建民. 齿轮箱振动的故障诊断与分析[J]. 武汉工程大学学报, 2011,33(12):70-72.

[2] Hoseini M, Mandal M K, Zuo M J, et al. Gearbox fault diagnosis using Hilbert transform and segmented regression.Proceedings of the Fifth International Conference on Condition.Monitoring & Machinery Failure Prevention Technologies[J]. Edinburgh Scot-land UK,2008(18):650-656.

[3] 陈汉新, 王庆军, 陈绪兵, 等.基于解调振动信号特征提取齿轮箱的故障诊断[J]. 武汉工程大学学报, 2010, 32(9): 67-77.

[4] 贺文杰, Bajolet Julien, Yoann Plassard, 等. 基于EMD和FFT的齿轮箱故障诊断[J]. 武汉工程大学学报, 2011, 33(1): 65-70.

[5] 尚云飞, 陈汉新, 孙魁. 面向齿轮箱故障诊断的序贯概率比检验理论和方法[J]. 武汉工程大学学报, 2011, 33(12): 65-69.

[6] Li Zhen, He Zhengjia, Zi Yanyang, et al. Rotating machinery fault diagnosis using signal-adapted lifting scheme[J].Mechanical Systems and Signal Proce-ssing，2008,22(3):542-556.

[7] Yuan Shengfa, Chu Fulei. Fault diagnosis based on support vector machines with parameter optimisationby artificial immunisationalgorithm[J].Mecha-nical Systems and Signal Processing,2007,21(3):1318-1330.

[8] Chen H X, Chua P S K, Lim G H. Vibration Ana-lysis With Lifting Scheme and Generalized Cross Validation in Machinery Fault Diagnosis[J]. Journal of Sound and Vibration, 2007,301(3-5):458-480.

[9] Cheng Junsheng, Yu Dejie, Yang Yu. Energy oper-ator demodulating approach based on EMD and its application in mechanical fault diagnosis[J]. Chinese Jounal of Mechanical Engineering,2004,40(8):115-118.

[10] Qian S, Chen D. Signal representation using adap-tive normalized Gaussian functions[J]. Signal pro-cessing, 1994,36(1):1-11.

[11] 张丽平. 粒子群优化算法的理论及实践[D]. 杭州: 浙江大学, 2005.

[12] Angeline P J. Evolutionary Optimization Versus Particle Swarm Optimization: Philosophy and Perf-ormance Differences[J]．Proc Seventh Annual Conf-erence On Evolutionary Programming，1998，48(17):256-260．

[13] 李桂芝, 何万里, 钱伟懿. 基于改进粒子群算法优化电梯群控系统[J]. 渤海大学学报: 自然科学版, 2007, 28(1): 42-45.

[14] Fakhfakh T, Chaari F, Hadder M. Numerical and Experimental Analysis of a Gear System with Teeth Defects[J]. International Journal of Advanced Manufacturing Technology,2005,25(5-6):542-550.