磷矿堆场多目标优化配矿模型

李志国，崔周全，张电吉，陈鹏能

(1.云南磷化集团，云南 昆明 650600；2.武汉工程大学环境与城市建设学院，湖北 武汉 430074)

0 引 言

配矿是矿物资源质与量的相互协调与均衡，是一项多阶段的工艺过程，它贯穿于从矿山规划、计划到矿山生产整个过程和各个生产环节.堆场配矿是这一整体系统的重要环节之一，特别是对像磷矿矿石特征各异，原矿品质差异大，脉石对选矿、磷化工影响严重的一类矿产资源，堆场配矿具有举足轻重的地位[1].

对配矿计划数学模型的分析和研究，国内外有很多研究成果可以借鉴.其解决方式也多种多样，比较成熟的技术如线性规划[2-9]、0-1整数规划法[10]、UM模型[11]、非线性回归分析等等.其中胡清淮[6]在建立线性规划模型基础上，对模型退化性进行了讨论，并借助计算机用逆矩阵单纯形法完成了求解计算；戚国安和舒航[7]对应用线性规划模型配矿中的随机误差进行了分析，通过计算期望产值，确定理想配矿品位，并指出配矿质量控制对矿山经济效益有着重要影响.张立溥和胡清淮[8]分析了配矿模型中的目标函数系数灵敏度的重要性.刘文生应用模糊线性规划的方法[9]，分析了矿山企业生产过程中包含许多非确定性的因素和模糊特征的主体网络系统.

以上线性规划等配矿构模一般以经济效益为目标，对产能、有益有害组分、非负性等进行约束，建立模型求解.而在矿山实际配矿过程中，配矿目标往往不只一项，且很多情况下，各子目标可能是相互冲突的，非多目标规划模型就显得无能为力.众多学者尝试了多目标规划模型[12-16]通过引入模糊方法等，对目标重要性处理开展了大量研究[17-19]，取得一定成果.

然而，常规的多目标解算方法不能有效地解决诸多配矿实际问题及要求[20]，模糊多目标等算法[17-19]较为复杂，现实生产中，多目标规划仍未能成为配矿领域内实用性及通用性更强的方法.目前仍以线性构模为主要手段，存在着不足之处.

笔者基于磷矿堆场实际生产工艺过程，建立堆场多目标配矿模型，较完整描述该工艺阶段需要达到的配矿目标基础上，应用Matlab优化工具箱中多目标规划工具，实现了堆场配矿多目标规划模型简便、有效求解，实际操作性强.

1 多目标优化配矿模型

1.1 多目标优化原理

多目标优化问题(multi-objective optimization problem, MOP)又称为多标准优化问题.不失一般性，一个具有n个决策变量，m个目标变量的多目标优化问题[21]可表述为

(1)

其中，x=(x1,…,xn) ∈X⊂Rn为n维的决策矢量，X为n维的决策空间，y=(yl,…,ym) ∈Y⊂Rm为m维的目标矢量，Y为m维的目标空间.目标函数F(x)定义了m个由决策空间向目标空间的映射函数；gi(x)≤0(i=1,2,…,q)定义了q个不等式约束；hj(x)=0(j=1,2,…,p)定义了p个等式约束.

对于多目标优化问题有如下重要定义[22-23]：

定义1(可行解)：对于某个x∈X，如果x满足(1)中的约束条件gi(x)≤0 (i=1,2,…,q)和hj(x)=0 (j=1,2,…,p)，则称x为可行解.

定义2(可行解集合)：由X中的所有的可行解组成的集合称为可行解集合，记为Xf，且Xf⊆X.

定义3(Pareto占优)：假设xA,xB∈Xf是式(1)所示多目标优化问题的两个可行解，则称与xB相比xA是Pareto占优的，当且仅当

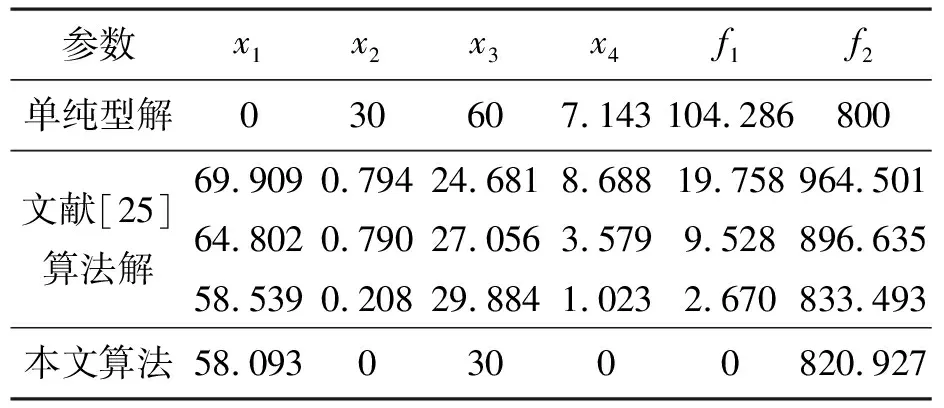
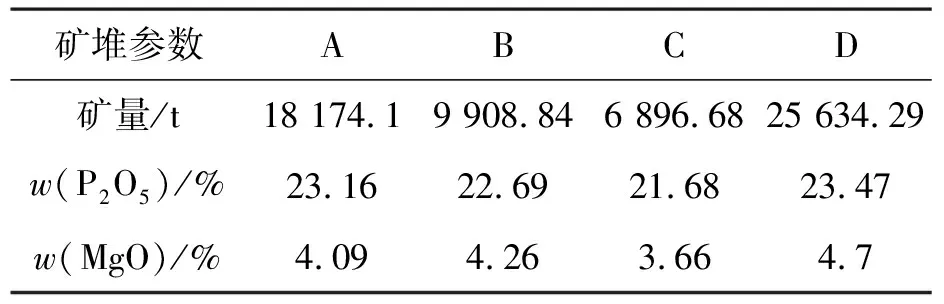
∀i=1,2,…,m,fi(xA)≤fi(xB)Λ∃j=1,2,…,m,fj(xA)

(2)

记作xA≻xB，也称为xA支配xB.

定义4(Pareto最优解)：一个解x*∈Xf被称为Pareto最优解(或非支配解)，当且仅当满足如下条件:

∃x∈Xf∶x≻x*

(3)

定义5(Pareto最优解集)：Pareto最优解集是所有Pareto最优解的集合，定义如下:

(4)

多目标优化问题各子目标之间具有较强的耦合性及冲突性，多个子目标不可能同时达到最优，只能在他们中间进行协调和折中处理，使各子目标函数尽可能达到最优.Pareto最优解即是一个可以接受的“不坏”的解，通常一个多目标问题会具有多个Pareto 最优解.在实际应用问题中，必须根据对问题的了解程度和决策人员的个人偏好，从 Pareto 最优解集中挑选一个或一些解作为多目标优化问题的最优解.

1.2 磷矿堆场多目标优化配矿模型

随着磷矿逐年开采，富矿越来越少，磷矿石品质逐渐变差，越来越多的矿石采出后不易直接进入浮选流程.通常运至堆场分堆堆放，根据入选原矿要求进行矿石混配后再进入破碎—磨浮流程.

入选原矿一般要求满足各组分指标的同时，最大限度利用矿石.

假设有n堆原矿参与配矿，各堆矿量为Mi吨(i=1,…,n)，主要品质指标为P2O5、MgO及倍半氧化物，目前考察矿山倍半氧化物均满足矿石入选要求，该配矿模型暂不考虑倍半指标要求，故考虑品质参数如下：

pi为第i堆原矿石P2O5的含量，%，(i=1,…,n)；

mgi为第i堆原矿石MgO的含量，%，(i=1,…,n)；

参照多目标规划一般形式(1)可对配矿模型表示入下：

(5)

式(5)中：mi为决策变量，即第i堆矿石配矿量，吨.其中，目标函数具有理想目标值.

通常提高矿石P2O5的含量，MgO等杂质的含量将会升高，两目标相互冲突，即某一子目标的改善将引起其他子目标性能的降低.故模型为典型多目标规划问题.

2 多目标优化模型解算

处理多目标优化的方法比较多，如约束法、评价函数法、功效系数法等[24].随着计算机应用技术的发展，各种用于多目标优化解算的软件层出不穷.Matlab作为三大数学软件之一，其强大的科学计算功能和覆盖面广、专业性强的工具箱发展成为适合多学科、跨平台的大型实用科学计算软件，也为最优化问题的解决提供了有力工具.

2.1 基于Matlab多目标优化模型解算技术

Matlab优化工具箱功能涵盖：无约束条件非线性极小值；约束条件下非线性极小值，包括目标逼近问题、极大-极小值问题和半无限极小值问题；二次规划和线性规划问题；非线性最小二乘逼近和曲线拟合；非线性系统的方程求解；约束条件下的线性最小二乘优化；复杂结构的大规模优化问题等.其中对于多目标规划问题，Matlab可以利用不同函数进行求解.例如：在评价函数法中我们所得最后评价函数为一线性函数，且约束条件也为线性函数，则可直接利用工具箱提供的线性规划函数linprog进行求解；若得到评价函数为非线性函数，则可利用fmincon函数求解；如果采用极大极小法求解，则可直接利用工具箱中fminimax函数求解.

对于式(5)表示的配矿模型，原矿石P2O5及MgO的含量均有一确定目标值，可直接调用fgoalattain函数求解.其一般调用格式如下：

[x,fval]=fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,options)

其中，x、fval为函数返回的决策变量及目标函数向量值；fun为需要最小化的目标函数；x0为求解的初始值；goal为目标函数期望值；weight为目标权重，其他相关信息详见Matlab优化工具箱手册.

选厂对入选原矿不同组分的品质要求，可以通过对goal与weight参数的控制设置来实现.输入参数中的weight变量为权重向量，可控制低于或超过函数指定目标的相对程度；设置硬约束，以表示某一组分含量严格达到目标值.

2.2 解算实例

为了验证该算法的有效性，计算文献[25]实例如下:

目标规划模型为：

(6)

f1(x)和f2(x)在同一优先级下，f1(x)的上限值为20，f2(x)的下限值为800，采用本文解法及文献[25]解法结果比较如表1.

表1 多目标规划不同解算方法结果对比Table 1 Results comparison during different solving method for multi-objective optimization

从求解结果对比可以发现，单纯型法得到的解不是决策者满意解，而采用Matlab优化工具箱fgoalattain函数得到的解及文献[25]遗传算法得到的三个解均为决策者满意解.并且，针对该类具有目标值约束或确定期望值的特殊小型多目标规划问题，fgoalattain函数具有参数设置方便，求解简单的优势.

3 磷矿堆场多目标优化配矿实现

针对某磷矿堆场多目标优化配矿模型，应用Matlab优化工具箱中多目标优化函数求解实验如下：

某矿浮选厂堆场一月份共堆存来自4处不同矿源的原矿待处理，各堆参数如表2所示：

表2 某矿堆场入选原矿库存情况表Table 2 Inventory of raw ore in a stockyard

选厂入选原矿石主要指标要求如表3所示：

表3 某浮选厂入选原矿品质要求Table 3 Ore quality requirements for mineral processing

假设A、B、C、D矿堆配矿量分别为：m1、m2、m3、m4吨，根据式(5)构建优化模型如下：

(7)

设置目标函数期望值为60 613.91，23.05,4.2；严格控制P2O5含量不低于23.05%，MgO不超过4.2%.应用fgoalattain函数解算结果如下：

m1=18 174.1，m2=0，m3=4 014.0，m4=8 333.4即A∶C∶D≈9∶2∶4

对应目标函数结果为：30 521.5，23.05，4.2；计算结果显示按照A∶C∶D=9∶2∶4混配后，可以得到P2O5含量23.05%，MgO含量4.2%的矿石30 521.5 t.实际配矿操作后，混配矿石30 290 t，实测P2O5含量23.05%，MgO含量4.19%.矿石主要指标均满足入选矿石要求，充分利用了低磷(C)及高镁(D)磷矿石，配矿效果明显.

4 结 语

a. 通过分析磷矿堆场配矿过程，选取P2O5、MgO质量指标及磷矿石最大限度利用为目标，以堆场资源量及决策变量非负为约束，构建了磷矿堆场多目标配矿模型.

b. 磷矿堆场多目标配矿模型简单、直观、较完整的描述了堆场配矿工艺过程及目的，很好体现了矿石充分利用的宗旨，符合资源节约型社会建设要求.

c. 应用Matlab优化工具箱多目标规划相关函数，实现了磷矿堆场多目标配矿模型简便、有效求解，证明了Matlab优化工具箱对类似堆场多目标配矿模型求解的有效性.

参考文献：

[1] 孙成斌．配矿对过磷酸钙生产的影响[J]．化工矿物与加工，2000(6):10-11,19.

[2] WILKE F L, REIMER T H. Optimizing the Short-Term Production Schedule for an Open-Pit Iron Ore Mining Operation [C]// Alfred Weiss. Computer Methods for the 80’s in the Mineral Industry. New York: Society of Mining Engineers, 1979:642-646.

[3] 易丽平，王李管，房智恒．线性规划在露天配矿中的应用[J]．现代矿业，2010，26(1)：42-44.

[4] 肖建华，郁钟铭．磷矿生产配矿研究[J]．矿业工程，2009，7(2)：25-26.

[5] 侯煜．线性规划法在露天矿配矿领域的应用[J]．矿业工程，2006,4(1)：22-24.

[6] 胡清淮．线性规划在矿山配矿问题中的应用[J]．系统工程，1983,1(2)：57-62．

[7] 戚国安，舒航．配矿优化随机误差分析[J]．金属矿山，1992(3)：54-56．

[8] 张立溥，胡清淮.多矿山综合配矿线性规划问题研究[J].武汉化工学院学报，2004,26(1):88-91.

[9] 刘文生.数学规划在露天矿生产规划中的应用[D].唐山:河北理工大学，2004.

[10] 王克让，陆厚华，杜雅君.利用0-1整数规划法进行原矿配矿[J].轻金属,1997(12):13-15.

[11] 林启太.未确知数学在研究混合配矿中的应用[J].系统工程理论与实践，2002(1):99-102.

[12] 徐玖军,李军.多目标决策理论与方法[M].北京:清华大学出版社,2005.

[13] Arenas M, Bilbao A, Rodriguez M V. Solving a multi-objective possibility problem through compro-mise programming[J].Eur J Oper Res, 2005, 164: 748.

[14] 唐加强,汪定伟.模糊优化理论与方法的研究综述[J].控制理论与应用,2000,17(2): 159.

[15] Narasimhan R. Goal programming in a fuzzy envir-onment[J].Decis Sci, 1980, 11:325.

[16] Gao J, Liu B. Fuzzy multilevel programming with a hybrid intelligent algorithm[J].Comput Math Appl, 2005, 49:1539.

[17] Chen L H, Tsai F C. Fuzzy goal programming with different importance and priorities[J].Eur J Oper Res, 2001, 133:548.

[18] Liu B, Liu Y K. Expected value of fuzzy variable and fuzzy expected value models[J].IEEE Trans Fuzzy Syst, 2002, 10(4):445.

[19] 徐铁军，杨鹏．基于模糊多目标优化算法的矿山配矿优化[J]．北京科技大学学报，2009,31(11)：1363-1367.

[20] Xu T J,Yang P. Application of improved Genetic algorithm in mine ore blending[C]∥The 3rd Interna-tional Symposium on Modern Mining&Safety Techno-logy Proceedings. Fuxin:Liaoning technical university, 2008, 8:174.

[21] Deb K. Multi-Objective Optimiution Using Evolutionary Algorithms[M]. Chichester: John Wiley&Sons, 2001.

[22] TSAIS J , SUN T Y, LIU Chan-cheng , et al . An improved multiobjective particle swarm optimizer for multiobjective problems[J]. Expert Systems with Applications , 2010 , 37( 8) : 5872-5886.

[23] 公茂果，焦李成，杨咚咚，等. 进化多目标优化算法研究[J]. 软件学报,2009,20(2):271-289.

[24] 李明.详解MATLAB在最优化计算中的应用[M].北京:电子工业出版社,2011.

[25] 赖红松，董品杰，祝国瑞．求解多目标规划问题的Pareto多目标遗传算法[J]．系统工程，2003，21(5)：24-28．