基于聚类算法的MWD泥浆脉冲信号识别研究*

涂 兵，李德胜*，林恩怀

(1.北京工业大学机械工程与应用电子技术学院，北京100124;2.北京普利门电子科技有限公司，北京100041)

石油随钻测量(MWD)系统中，井下数据传输和地面数据接收是随钻测量中的关键技术。目前MWD中信号的传输方式主要有电磁波和钻井液压力波2种[1]。电磁波传输信号由于随着地层深度地增加，信号的幅值衰减严重，并且地质构造的差异化也可导致信号的幅值衰减程度不一，因而信号的传输速率只能以较低的频率发送，并且传输距离较短[2]。钻井液压力波与电磁波信号的传输速率相比具有可靠性更高、传输距离更远等特点，因此利用钻井液压力波进行通信是目前MWD中采用的一种普遍方式[3－8]。但是，由于MWD信号传输介质易受到外界各种噪声的干扰[7]，因此从被各种噪声淹没的信号中提取出有用的信号成为亟需解决的问题。文献[4]对泥浆脉冲信号中的泵噪声、钻井噪声、脉冲噪声、发射噪声等进行了分析。文献[5]采用小波变换对泥浆脉冲信号进行了处理，将7种常用的小波基函数选取不同参数后分解重构的信号与原始信号进行了比较，通过相关系数的大小选定了适合处理该信号的最佳小波基函数及其参数。文献[5]采用了对线性滤波算法还原脉冲信号的方法，在此基础上利用一种非线性“平顶消除”的方法对泥浆脉冲信号进行了处理。文献[6]和文献[8]采用了相关小波去噪处理的方法。文献[9]采用了相关滤波处理的方法。上述文献所采用的方法主要集中在对信号的去噪处理上，并且主要针对的是脉冲位置组合(PLM)方式的信号处理，对去除噪声的泥浆脉冲信号识别没有做相关的阐述。本文对基于曼彻斯特编码方式的泥浆脉冲信号的提取和识别算法进行了分析和研究;运用了模糊聚类算法对采集的泥浆脉冲信号进行了识别。

1 曼彻斯特编码的泥浆脉冲信号分析

1.1 噪声分析

在特定频率的控制下，曼彻斯特编码方式对井下状态等信号进行数据通信时，由于井下条件复杂，信号传输过程中受到各种噪声的干扰导致地面解码系统采集到的压力波信号幅值很小，其中泥浆压力波主要的噪声有:泵噪声、钻井噪声、脉冲噪声、反射信号等[1，5]。

图1是采集的井上泥浆压力波波形，图2是井上泥浆压力波频谱，从图1和图2可以看出，泥浆压力波信号包括有基值波动和幅度较大的高频分量噪声，有用信号的频谱范围在0.2 Hz～1 Hz，噪声分布较宽。

图1 泥浆压力波波形

图2 泥浆压力波信号频谱

高频噪声主要是由3缸单作用泵产生的，幅度无规律性变化;低频噪声主要是由泵冲引起的，信号的频率为0 Hz～0.2 Hz，在信号频谱范围内，噪声幅度小于信号幅度。干扰幅度变化的不规则使得信号频率和噪声、干扰的频谱出现重叠，从而给剔除噪声及复原脉冲信号带来了很大难度。

1.2 波形识别前自适应滤波去噪

目前去除泥浆信号噪声的主要方法包括:常规线性滤波，小波滤波等。运用小波分析时，阈值往往难以界定，实现有效处理相对困难[8－11]，本文采用NLMS自适应滤波的方法去除噪声，与小波等目前常用的泥浆脉冲信号处理方法相比，NLMS自适应滤波具有较好的适应性、运算量较小，收敛速度较快[12－14]。图3是本文采用的基于 NLMS自适应滤波算法的原理框图。实际应用中，采用泥浆脉冲传输协议中的同步头来训练自适应滤波器。在训练过程中，由于信源所发送的内容已知，自适应滤波器不断调节参数使得输出和已知的正确内容误差最小。

图3 自适应滤波框图

NLMS算法如式(1)所示。

x(n)为含同步头噪声信号，d(n)为事先设置的训练序列，采用的为同步头数据位“01111110”。mu采用0.001，w(n)采用长度为 50，初始化为 0，经过NLMS[12－13]的自适应滤波后的波形为如图4所示。

图4 自适应滤波后泥浆压力波波形

从图4中看出，信号的噪声在大于0.8 Hz时已经被消除，能大大提高信噪比，为下一步信号的识别打下基础。信噪比:SNR=10lg(S/N)2=49.09 dB(S为去噪后的信号，N为噪声信号)。

2 聚类算法识别研究

2.1 聚类算法识别样本模型

曼彻斯特编码的规则为在一个比特周期内，信号由高电平到低电平代表的数据位为“1”，相反为“0”。井下DSP对数据进行曼彻斯特编码时，如果存在有连续的“11”或者“00”位时，泥浆脉冲波形在一比特周期内连续上升或者下降波形，在连续的上升波形识别也为“1”，相反为“0”。采用3比特周期内的泥浆压力波进行波形识别时，波形形状存在有16种形状特征，对应的二进制编码值为000～111。图5是依次对16种形状进行编号和二进制编码。

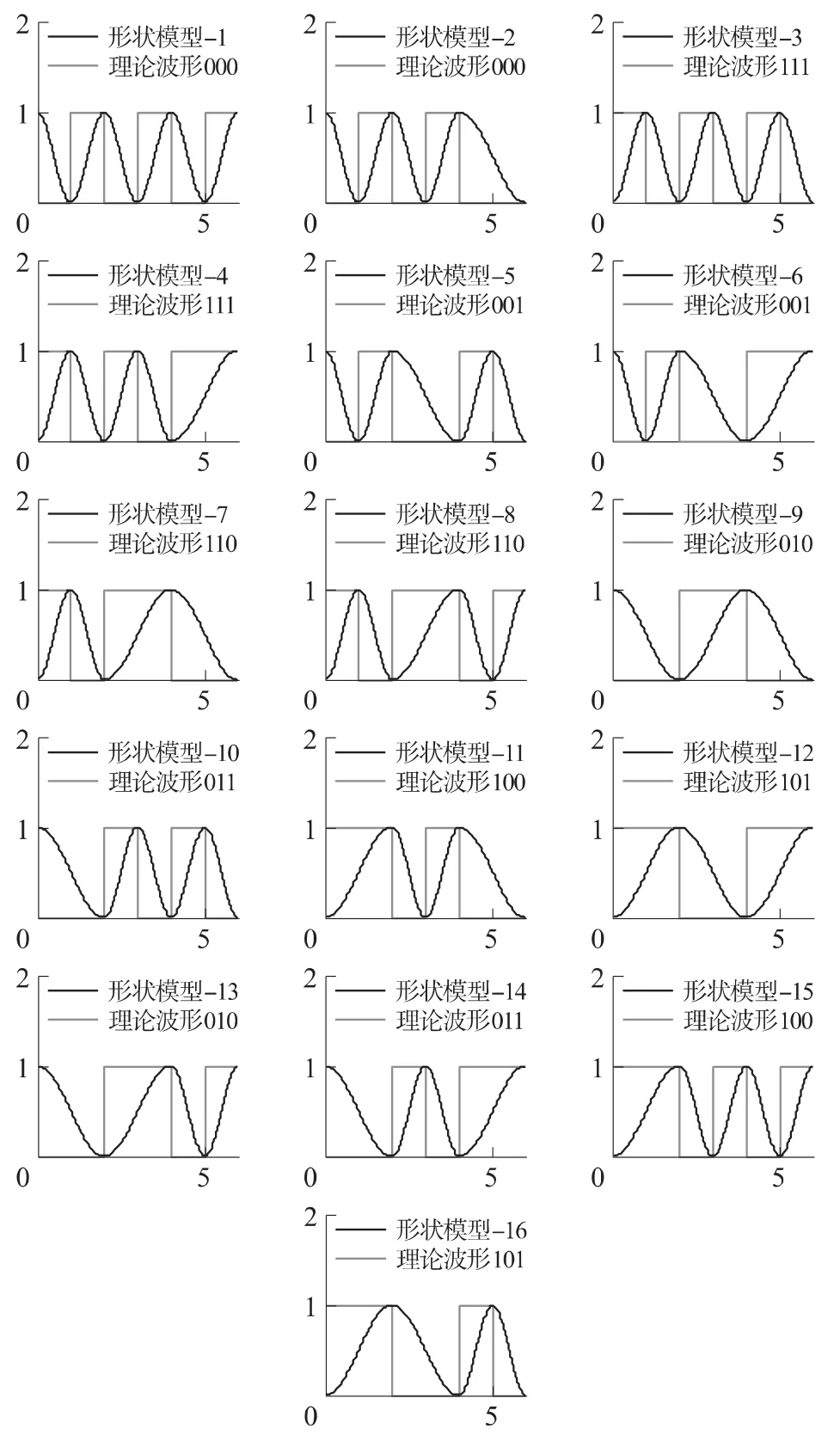
图5 16种参考波形模型和分类

2.2 聚类识别计算

16种参考模型设定后，然后对NLMS自适应滤波后的波形进行波形识别。波形识别采用模式相似性测度方法[14－15]。参考模型特征向量为 Xi=(xi1xi2，…，xin)T、经过 NLMS处理的实时采样泥浆脉冲特征向量为Xj=(xj1，xj2，…，xjn)T。采用欧式距离、特征是二值时的夹角余弦、和具有二值特征的Tanimoto方法来计算两类数据的相似程度。

欧式距离D:

特征是二值时的夹角余弦S:

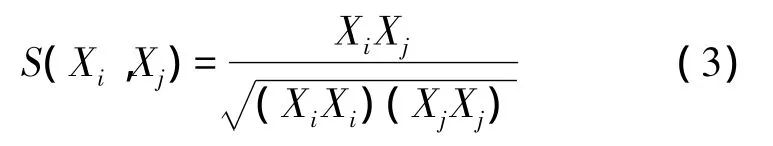
具有二值特征的Tanimoto测度T:

在采用聚类算法对实际信号处理时，窗口的滑动是以1比特周期内滑动进行依次识别，图6为截取的自适应波后泥浆脉冲信号的两类波形进行分析图形。Dij越小、S和T越大表示两类数据之间的波形越相似。基于以上理论采用以上3种识别算法对图6中的两类泥浆脉冲波形进行了识别。图7、图8、图9分别是与16种模型与图6现场泥浆脉冲信号进去去噪处理后采用欧式距离、特征是二值时的夹角余弦和具有二值特征的Tanimoto测度T值。

图6 截取分析两种形状波形

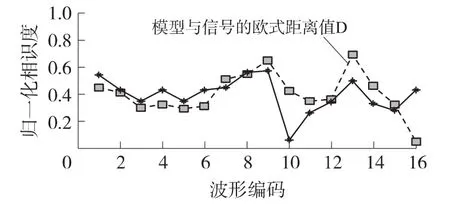
图7 模型与信号的欧式距离值

图8 模型与信号的特征二值夹角余弦值

图9 模型与信号二值特征Tanimoto值

从图7～图9中可以看出，截取分析图6中0～6 s 3 bit周期内待识别的泥浆脉冲信号分别进行以上3种聚类识别后在第16号波形模型上Dij上取得最小值，在S和T上取得最大值。因而得出要识别波形数据二进值为“101”;以1比特窗口进行滑动，对2 s～8 s内的泥浆脉冲信号进行聚类识别，得到在第10号数据编码上Dij上取得最小值，在S和T上取得最大值，因而得出要识别的波形二进值为“011”。通过以上3种聚类分析方法可以有效的对泥浆脉冲信号进行识别。在实际工程应用最终判断泥浆脉冲信号数据位为“0”还是“1”时，在采用以上3种聚类算法计算后，选用多数表决机制来最终确定数据位。

2.3 识别准确率估计

识别准确率从下面3方面进行估计:①传输数据都应满足偶校验位。②与现场测试时国外的仪器同时进行数据的比较。③地面进行算法仿真，截取不同井深和时间数据进行了去噪和波形识别算法的验证。通过以上几点验证了此方法的识别准确率达到了98.5%以上，能满足工程应用的要求。

3 现场实验结果

模糊聚类识别算法在华北油田进行了现场实验。现场实验仪器如图10所示，图10左侧是采用聚类算法的地面解码机，图10右侧是Sperry_Sun公司的地面解码机。实验目标井是3.5 km深，泥浆粘度为10 mPa·s，实验从2 km开始进行定向测量。

图11是截取的2 km实验原始波形。图12是对2 km波形的复原效果图。表1是现场进行实验时截取的一段数据，实验数据分别为采用模糊聚类算法解码数据和Sperry_Sun公司的解码数据。在NLMS自适应滤波算法去噪的基础上，模糊聚类识别算法能较完整正确的解出泥浆脉冲信号，误码率低于 1.5%。

图10 现场实验图片

图11 泥浆压力波原始波形

图12 识别后的复原方波信号

表1 实验结果数据统计表

4 结论

(1)通过对曼彻斯特编码泥浆脉冲信号进行了分析，将NLMS自适应滤波算法应用到了泥浆脉冲信号的去噪处理上，为获取高质量的复原曼彻斯特编码波形奠定了基础。

(2)在NLMS自适应滤波算法对含有噪声的泥浆脉冲信号进行了有效去噪的基础上，分析了曼彻斯特编码脉冲信号特征，建立泥浆脉冲信号识别模型，运用聚类识别算法对泥浆脉冲波形进行了识别，试验结果表明该方法能有效的提高识别正确率。

(3)通过对现场试验的验证。该方法能比较准确地解出井底的各种信号，具有误码率低，解码操作方便，在钻井液脉冲信号处理中具有广阔的前景。

[1]Tu Bing，Li Desheng，Lin Enhuai.Research on MWD Mud Pulse Signal Extraction and Recognition[J].2011 IEEE International Conference on Mechatronics and Automation，2011，7(1):2004－2008.

[2]苏义脑，窦修荣.随钻测量、随钻测井与录井工具[J].石油钻采工艺，2005，27(1):74－78.

[3]韩军，柴勤忠.泥浆信道无线随钻系统信号检测的数字信号处理方法[J].石油大学学报(自然科学版)，1994，18(2):96－101.

[4]赵建辉，王丽艳，盛利民，等.去除随钻测量信号中噪声及干扰的新方法[J].石油学报，2008，29(4):596－600.

[5]张恒，李安伟，李传伟，等.基于离散平稳小波变换的无线随钻系统测试信号处理[J].石油钻探技术，2007，35(2):49－51.

[6]张恒，李安宗，李传伟，等.钻井液波信号处理方法比较[J].石油钻采工艺，2007，29(2):84－90.

[7]Noureldin A，Irviner Halliday D，M intchev M P.Measurment while Drilling Surveying of Highly Inclined and Horizontal Well Sections Utilizing Single Axis Gyrosensing System[J].Mearurement Science and Technology，2004，15(12):2426－2434.

[8]张伟，师奕兵，卢涛.无线随钻泥浆信号小波包去噪处理[J].电子测量与仪器学报，2010，1(24):80－84.

[9]Chen Wenyuan，Fang Bin，Wang Yi.MWD Drilling Mud Signal De-Noising and Signal Extraction Research Based on the Pulse-Code Information[C]//Proceedings of the 2010 International Conference on Wavelet Analysis and Pattern Recognition，2010，6(1):244－249.

[10]周挺，胡斌杰.基于小波变换的自适应多聚焦图像融合算法[J].传感技术学报，2010，23(5):1271－1275.

[11]罗海勇，李锦涛，赵方.基于均值漂移和联合粒子滤波的移动节点定位算法[J].传感技术学报，2009，22(3):378－386.

[12]王伟，张广明，王祥华.基于自适应滤波算法的电压波动检测与跟踪[J].电测与仪表，2011，48(7):20－23.

[13]冯冬清，孙长峰，费敏锐.一种新的变步长LMS算法研究及其应用[J].自动化仪表，2007，28(8):67－69.

[14]Wang Weiyi，Rong Yicheng，Gong Youmin.Fuzzy Clustering Based Recognition and Simulation for Dynamic Wave Pattern of Mould Breakout[J].Journal of System Simulation，2003，4(15):472－475.

[15]倪永州，田跃.一种快速模板匹配的波形识别算法[J].传感器世界，2006，1(4):31－34.