无线信道模型研究与展望(一)

李 萌，孙恩昌，张延华

(北京工业大学电子信息与控制工程学院，北京 100124)

0 引 言

随着通信技术的发展，无线通信技术成为了最为复杂的通信方式之一。无线通信系统的工作环境复杂，信号从发射机到接收机的过程需要借助无线信道来完成。信道是连接发射机和接收机的媒介，是电磁波传播所经过的路径。无线信道并不像有线信道那样是可见的，它与有线信道的区别在于有线信道是按照固定的路径进行传播，而无线信道是多径传播，也就是从发射机到接收机存在着许多条路径，传播环境也比较复杂。

信号的传输过程会存在着各种不同的相互作用体，如山丘、树木、墙壁等，从而发生“阴影效应”。同时，信号传输过程中的多点反射会产生电平快衰落和时延扩展;由于信号传播经过了多径效应的影响，简单的接收机无法辨别不同的多径分量，而只是简单的将他们叠加起来，所以导致分量之间相互干涉。

根据实际情况建立合适的信道模型，对研究无线通信系统的特征和性能具有重要的意义。通过对常用的典型信道模型进行回顾、总结与展望，归纳出几种典型信道模型的适用范围、信道特点和相关计算公式等，并通过不同模型之间的参数对比，总结出不同信道模型的特点和性能，为不同环境选用合适的信道模型提供参考。

1 无线通信信道模型的基本内容

信号经过不同长度的路径到达接收端，使得接收信号脉冲宽度扩展的现象，称为时延扩展。多径信道时延扩展等于最先到达信号分量和最后到达信号分量之间时间延迟。如果这种时延扩展的大小和信号带宽的数值相比很小，那么接收信号在时间上的扩展也比较小。然而当它相对于信号带宽的倒数值比较大时，接收信号的时域波形就会被明显展宽，这有可能造成严重的信号失真［1］。

多径信道另一个特征是其时变性。时变性来源于发射机或接收机的运动或者信道媒介的相对运动，这种运动使传送路径中形成多径传播的那些反射点的位置随时间变化。

目前已经建立了许多多径模型，用以说明移动信道的观测统计特性。下面就几种典型的信道模型进行回顾与总结。

2 几种常用的无线通信信道模型

2.1 Okumura-Hata 模型［1］

该模型是国际公认的大区制和宏小区制模型，预测和测试的路径损耗偏差为10 ～14 dB。在城区环境的预测和模拟信号强度最广泛、使用最多的路径损耗模型是Okumura-Hata 模型。这个模型的有效使用范围是频率在500 ～1500 Hz，接收端距离基站大于100 m，基站的天线高度要大于30 m。此模型估计的最大频率能达到2000 Hz。通过许多实验发现，该模型不适合天线高度过低的基站。同时，此模型在丘陵、树木繁茂的地区也不适用。

2.1.1 平坦地形大城市地区中值路径损耗［1］

Okumura 模型中平坦地形大城市地区的中值路径损耗(dB)公式为

式中，Lbs为自由空间路径损耗

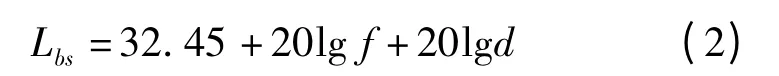
Am(f，d)为大城市地区当基站天线高度hb=200 m，移动台天线高度hm=3 m 时相对于自由空间的中值损耗;Hb(hb，d)为基站天线高度增益因子(dB)，即实际天线高度相对于标准天线高度hb=200 m 的增益，为距离的函数;Hm(hm，f)为移动台天线高度增益因子(dB)，即实际移动台天线高度相对于标准天线高度hm=3 m 的增益，它是频率的函数。

2.1.2 其他环境或不规则地形的中值路径损耗［2］

以上述环境作为研究基础，对不同的传播环境和其他不确定的环境所导致的各种因素，用修正因子进行修正，就可得到不规则地形和不同环境的中值路径损耗，用下式表示

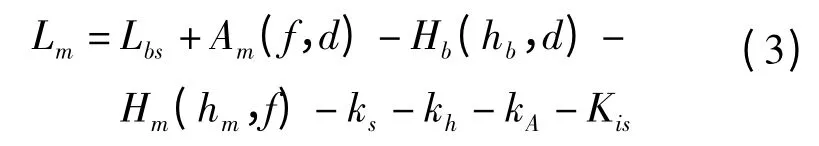
式中，ks为郊区修正因子;kh为丘陵地形修正因子;kA为斜坡地形修正因子;kis为水陆混合传播路径修正因子。

2.2 COST 信道模型［3，4］

欧洲科学和技术合作组(COST)研究了对于频率为2 GHz 的扩展Hata 模型，并定义如下

式中，在中小城市或者郊区环境下，CM为0 dB;而在大城市，CM为3 dB;其余参数都与之前设置相同。这种模型仅限于下列参数范围［3］

载波频率/GHz 1.5 ～2

基站天线高度/m 30 ～300

移动天线高度/m 1 ～10

距离d/km 1 ～20

COST231-Hata 模型为大型或小型宏单元设计，例如，基站天线高度高于相邻基站的屋顶［5］。

除了COST231-Hata 模型，欧洲科学和技术合作组还加入城市环境特点的视距(LOS)和非视距(NLOS)的情况。对于LOS，路径损耗为

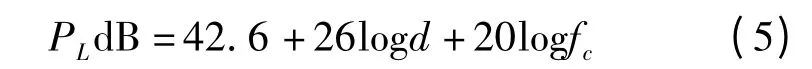
式中，d≥0.02 km;载波频率fc的单位是Hz［6］。

对于NLOS 的情况，路径损耗包括三个方面:自由空间的路径损耗L0，沿传播路径的信号多频叠加损耗Lmsd，以及屋檐边缘信号衍射损耗Lrts(屋顶到街道的衍射和散射损耗)

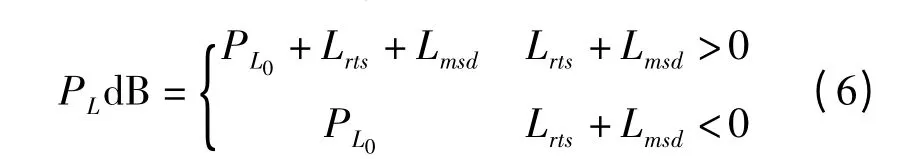
空间的路径损耗为

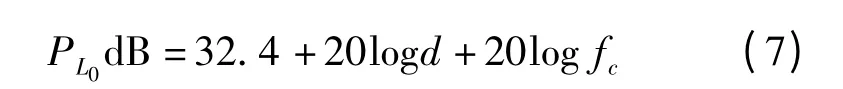
衍射损耗Lrts为

式中，w 为街道宽度，单位是m;Δhm是建筑物高度hroof和hm之差［7，8］。

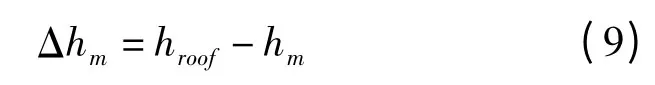
街道的方向是由实际的校正因子Lori决定［2］

近期，亚洲水泥、中国建材代表重回山水水泥董事会，山水集团也顺利解决了工商登记、公章接管等问题。山水水泥连续发行可转股债券累计5亿多美元，对企业金融风险化解起到了积极的影响。如果这部分债券全部转化为股权，所有认购人将持有16.33%山水水泥股份，天瑞集团持有的股份将会由28.16%稀释至23.56%，失去在股东大会上对特别决议案的一票否决权。天瑞集团随后以公平及公正为由，分别向开曼法院、香港法院提交了山水水泥清盘呈请。

多频叠加损耗Lmsd表示为

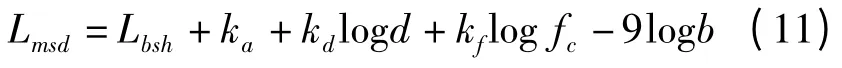
式中，b 为两个建筑物之间的距离;

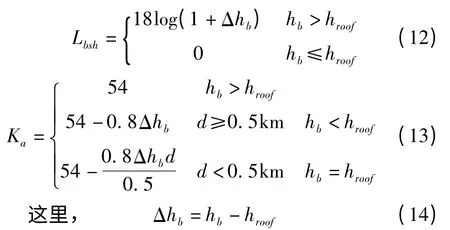
路径损耗取决于给定参数的频率Kd和距离Kf

该模型的有效范围为［4］

载波频率fc/MHz 800 ～2000

基站天线高度hb/m 4 ～50

移动天线高度hm/m 1 ～3

距离d/m 0.02 ～5

该模型假设曼哈顿街道网格(街道呈直角相接)，建筑物高度基本恒定，地势平坦，该模型不包括街道峡谷效应产生的导波，被磁场所影响［9，10］。

2.3 平坦衰落的Clarke 模型［11］

Clarke 建立了一种统计模型，其移动台接收信号场强的统计特性基于散射。该模型假设有一台具有垂直极化天线的固定发射机。入射到移动台天线的电磁场由N 个平面波组成，这些平面波具有任意载频相位、入射方位角及相等的平均幅度。其中，相等的平均幅度的基础在于不存在视距链路，到达接收机的散射分量经小尺度距离传播后，经历了相似的衰减［1，9］。

例如，一辆以速度v 沿x 方向运动的汽车接收到入射平面波。根据运动方向，选择在xoy 平面进行入射角度测量。由于接收机的运动，每个波经历了多普勒频移并同一时间到达接收机。也就是说，假设任何平面波(平坦衰落条件下)都没有附加时延。对第n 个以角度αn到达x 轴的入射波，多普勒频移为

式中，λ 为入射波的波长［12］。

到达移动台的垂直极化平面波存在E 和H 场强分量，分别表示为

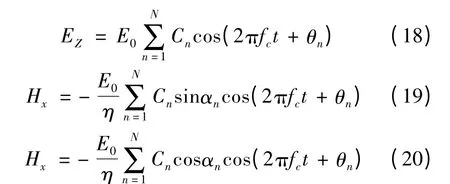
式中，E0是本地平均电场(假设为恒定值)的实际幅度值;Cn是不同电波幅度的实数随机变量;η 是自由空间的固有阻抗(377);fc是载波频率。第n 个到达分量的随机相位θn为θn=2πfnt+Φn［13，14］。

对E 和H 场的幅度进行归一化后，可得Cn的平均值，并由下式确定

由于多普勒频移与载波频率相比很小，因而三种场分量可建模为窄带随机过程。若N 足够大，三个分量Ez、Hx和Hy可以近似看作高斯随机变量。假设相位角在(0，2π)间隔内有均匀的概率密度函数，由莱斯分析可知，E 场可用同相和正交分量表示

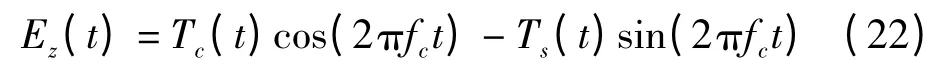
式中，

(未完待续)