航线团队旅客收益管理双层规划模型

徐 琪，徐月芳

（南京航空航天大学 民航学院，江苏 南京 210016）

团队旅客是航空公司客源的主要组成部分之一，是影响收益的一个重要因素[1]。关于团队旅客的管理问题在国外已经发展的很成熟，相关产品已经为企业的收益管理问题提供了高效的解决方案。比如美国的PROS软件可以解决在不替代高价票需求的情况下接受团队，制定最低可售价，定价时考虑风险因子，跟踪团队的取消或增加情况，通过在线工具进行团队旅客销售的谈判及管理，生成与旅行代理商的合同及条款等问题。专门针对航空公司的收益管理软件SABRE，通过将团队旅客调整到散客需求较低的航班上能够平均增加1%～2%的收益；改进客户服务，通过直接在线预订团队票降低成本；通过自动控制缩短团队请求的周期。国内关于团队旅客收益管理的文献较少，杨思梁，徐公达等做过一些定性研究但并未深入，高强提出了一个如何接受团队的静态优化模型[1]。高荣环发现在实际中单一航班上可用座位数可满足团队旅客需求，这一前提条件不是常常满足[2]。

当单一航班的可用座位数不能满足团队旅客需求时，如果将团队拆分在同一航线的不同航班上是一个非常值得研究的问题。将团队拆分在不同的航班上可提高航空公司的收益但从旅行代理商的角度来说增大了管理难度，团队拆分越散，旅行代理商的对拆团方案的接受度越低。从提高航线上整体收益和代理商可接受度两个效益背反的因素出发，利用双层规划的博弈特点建立模型对如何进行团队拆分进行定量分析，上层在EMSR－a对散客需求进行预测的基础上以航线上所有航班的总收益最大为目标，用下层规划以旅行代理商对拆团接受度最大为目标，运用熵权法计算出在影响因素下旅行代理商可接受度的综合得分，作为拆分团队的依据。最后，设计了分层迭代的算法，并结合实例验证了模型和算法的有效性。

1 问题描述

当单一航班上的可用座位数不能满足团队旅客需求的时候，将团队拆分在同一航线的不同航班上可有效提高航班的客座率增加收益。但团队拆分的同时对于旅行代理商来说不仅意味着增加了管理难度，也可能引起旅客满意度的下降。因此，航空公司在以收益最大化为目标进行团队拆分时也要兼顾到旅行代理商的可接受程度。基于这种关系，可以用双层规划模型（Bi－level programming）来描述，上层规划（U）描述为航空公司拆分团队时以航线总收益最大化为目标。下层规划（L）描述为航空公司将团队在分配在不同的航班上，其目标是尽量提高旅行代理商的可接受度。上层规划在散客预测的基础上从收益最大化角度给出航空公司一个拆分方案，Belobaba在1987年提出了著名的EMSR理论，此后多年虽然有多种变化，但基于EMSR的舱位控制策略几乎成了一种工业标准[3]。下层规划即根据旅行代理商的可接受度来决定拆分到哪些航班上多少人。某些航班可能因为航空公司收益高被选择，但在下层规划中可能因为旅行代理商出于某些因素的考虑而安排团队旅客较少，甚至为零。上层规划和下层规划反复的相互影响，既可增加航空公司的收益，且同时兼顾旅行代理商，有益于航空公司的良性发展。

2 建立团队旅客收益模型

2.1 模型假设

为了便于建立模型，文中建立如下假设：

1）航线上单一航班在散客预测的基础上剩余座位不能满足同一团队旅客的需求；

2）团队旅客不占用头等舱、商务舱座位；

3）不同舱位的散客需求呈正态分布且独立；

4）团队整体最多拆分在3个航班上。

2.2 模型建立

符号意义：

pgi：不同航班团队旅客的价格

ni：分配在不同航班上团队旅客的人数

ci：每个航班上散客人数

W：航班可用座位数

N：团队旅客总人数

pil：航班i上 l舱的的散客价格

D ：散客预测数量，Di=（di1，di2，…，dil），dil是散客在票价 l的需求，为独立正态分布，dil服从 N（μil，）分布上层规划的目标为航空公司的收益最大，目标函数如下：

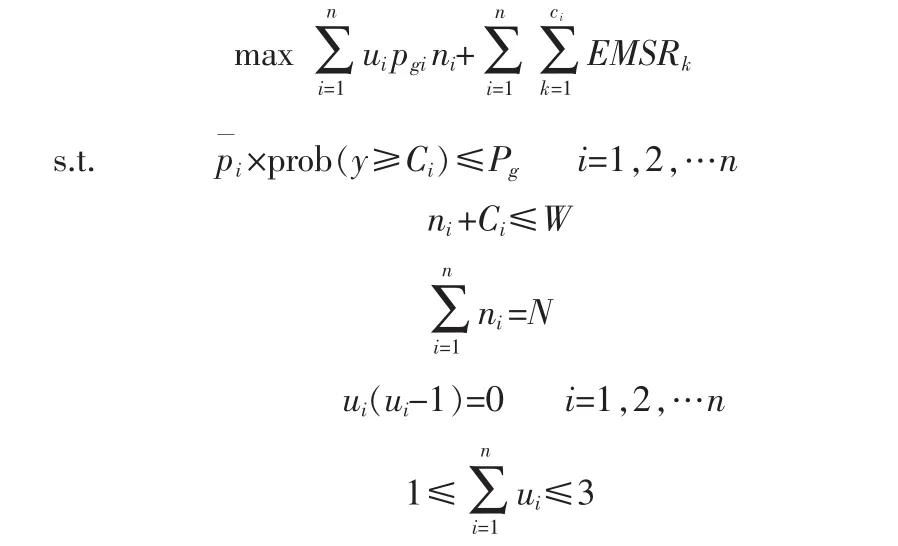
其中，

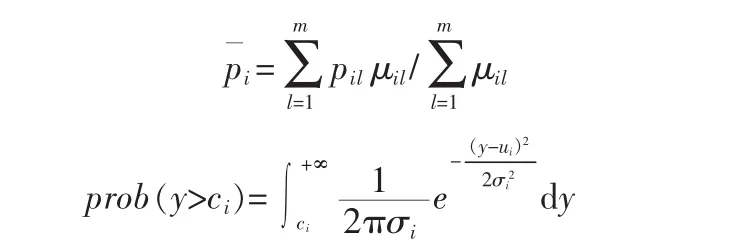
下层规划目标从考虑旅行代理接受拆团方案的程度方面来分配团队旅客：

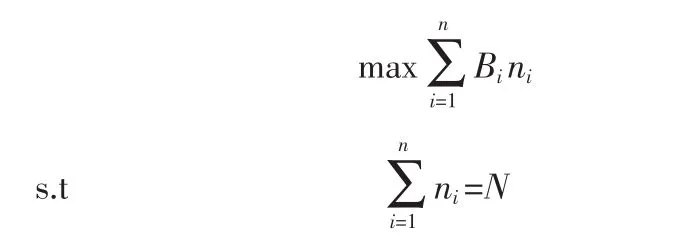
Bi为各影响因素的模糊评价值。

3 旅行社接受拆团方案的评估

熵（Entropy）是一个热力学概念，由Shannon引入信息论对系统的无需程度进行度量以及数据提供的有效信息量，在此模型中表示旅行社受各种因素影响程度的不确定性。人们可以根据熵值以及熵权的大小来进行决策，熵值越小熵权越大则该因素对决策起到了很重要的作用，对决策结果有较大影响。模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法，对于具有多种属性的事物需要进行综合评价，而对每种属性的评价又无法给出定量的评价值，使用模糊综合评价法可以有效解决这一问题[4]。

3.1 建立评价矩阵

构建n个样本m个影响因素的判断矩阵R′=（r′ij）nm（i=1，2，…n；j=1，2，…m。拆团对于旅行代理来讲管理成本的变化不大。导游的薪酬组合大致为：基本工资＋带团津贴＋“回扣”＋少量小费，由于每个导游带的人数比例固定，所以拆团不会导致导游人数的增加。总的团队旅客人数不变，所以即使拆团，只要合理的安排接送旅客，则车辆数量也无变化。不同的航班可能有的航班直达，有的航班转机，因此航空公司给出的折扣航班之间有差别，这是一个很重要的影响因素。航班准点率也是很重要的影响因素之一，这是旅客对服务满意度的重要评价指标之一[4]。拆团之后，旅行代理的旅游行程安排也会受到一定的影响，由于到达人员时间不一样，与最佳的行程开始时间有个偏差，旅行代理根据这个偏差对行程做进一步调整。所以影响旅行代理拆团的因素主要有折扣率、航班准点率和预期到达时间偏差这3个因素。

3.2 评价矩阵归一化

归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量[6]。 因评价矩阵中各影响因素的单位不一致，因而必须对数据进行归一化处理。

对于成本型指标：

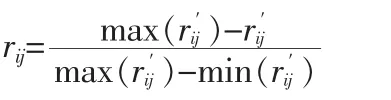
3.3 评价矩阵熵权的计算

各影响旅行商接受拆团方案的因素在指标上的值完全相同，熵值达到最大值1，熵权为0表示该指标未向决策提供任何有用信息；若某一因素在指标上的值相差较大，熵值较小，熵权较大时说明该因素提供了一定的信息量，对决策具有一定的影响，应重点分析[5]。

各因素对全部样本的比重为：

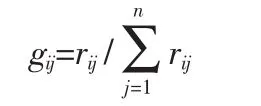
由评价特征矩阵R和综合权重向量W，利用模糊数学理论可以得到模糊综合评判模型：

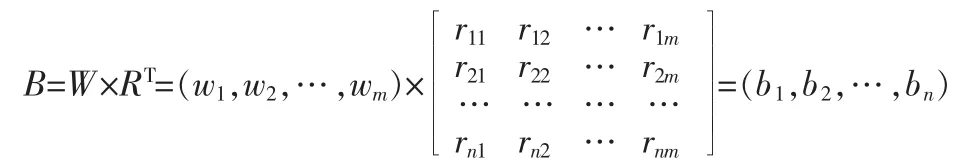
可以根据计算结果Bi的值来对旅行商对航班i的可接受度做出有效估计，Bi的值越大则旅行商对航班i的可接受度就越高。

4 模型求解

双层规划模型是由Bracken和McGill在1973年提出的，它是一个双层决策系统优化的数学模型，具有二层递阶结构的特点，避免了由于单一层次决策方法带来的弊端[7]。由于双层规划方法与传统的单层规划方法相比具有不可比拟的优势，具体表现在:1）可以同时分析决策过程中两个不同的、相互矛盾的目标；2）双层规划多价值准则的决策方法更接近实际情况；上层决策者和下层决策者都有各自的目标函数和约束条件，上层先给出一个决策变量，下层各子系统以这个决策变量为参量，根据自己的目标函数和约束在可能的范围内求得一个最优值，并将此最优值反馈给上层，上层再在下层的最佳反应的基础上，在可能的范围内求得整体上的最优解。一般说来，求解双层规划问题比较困难，Hansen（1992）对双层线性规划是强NP-hard问题给出了严格的证明，其后，Vicente（1994）年指出寻找局部最优解也是NP-hard问题，不存在多项式求解算法，其原因在于即使上下层中目标函数和约束函数都是线性的，它依然可能是一个并且非处处可微的非凸问题。目前双层线性规划算法主要有：极点算法，分枝定界法，K-T法，模糊数学算法[6]。这些算法都是针对特定的双层规划模型设计的，不具广泛性 ，针对某一实际问题还需设计适合的算法。针对本文模型特设计如下求解思路：给出上层规划决策变量一个取值，然后将其带入下层规划模型，求出下层规划模型的最优决策变量；将此最优决策变量代入上层规划模型，求出上层规划的最优值，重新带入到下层规划模型中，如此上下两层模型反复迭代一直到收敛于一个精度得出最优解。

本文中模型，上层规划的决策变量与下层规划的决策变量存在着内在联系，但很难直接求出两者关系的具体表达式，因此之前提及的分层迭代方法求解。其具体思路为：首先进行初始化，给出一个拆团的初始方案；设定一个航班选择的初始方案U将其代入下层规划L中，利用单纯形法算法求解下层规划问题，得团队旅客最优分配方案为N代入到上层规划中进行求解，获得新的航班选择方案U然后将其代入下层规划，再一次求解团队旅客配的最优方案N如此重复计算，最后收敛于双层规划模型的最优解。

具体步骤如下：

1）设定一个航班选择方案的初始解I0，令迭代次数k=1；

2）将初始解I0带入下层求最优解，得旅客分配方案N0及下层规划的目标函数值fn+1；

3）基于N0求解上层规划问题得到新的航班选择方案In+1及上层规划目标函数值Fn+1；

5）得双层规划模型的最优解和最优值。

该算法的关键是对每层问题分别进行求解，而单层规划模型的求解已经有较成熟的方法和计算机软件可用利用，利用Maple软件对模型进行求解取得了较好的实验结果。

5 算例分析

现有一45人的团队，在城市A到城市B有4个航班，航线上所用机型一致，经济舱可用座位数120。表1所示为各航班不同舱位价格、散客需求以及航班到达时刻。表2所示为影响旅行商接受拆团方案的因素，管理成本，旅客满意度以及票价。行程开始的预期时刻为15:00。

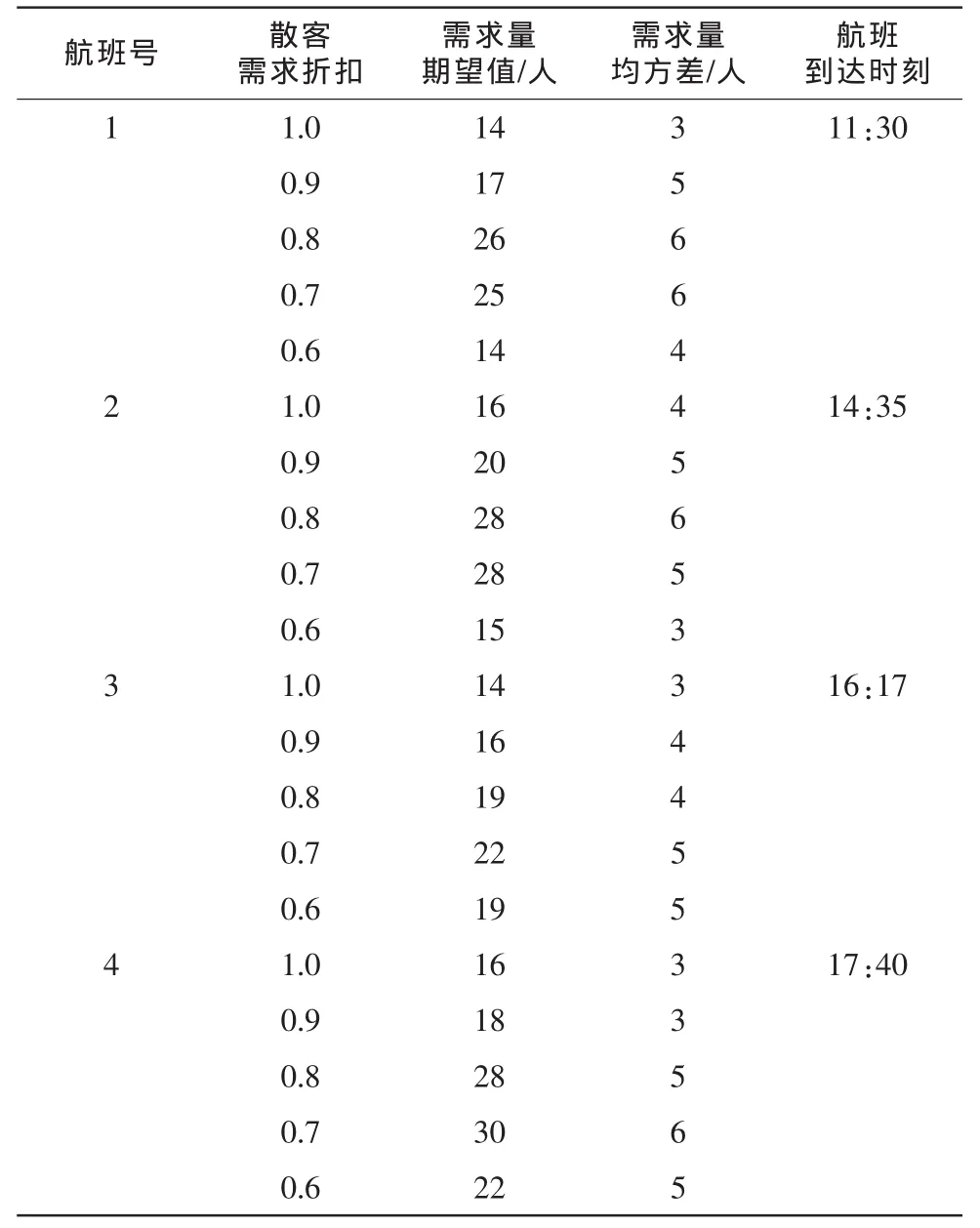
表1 航线上航班各舱位情况Tab.1 Status of different cabin

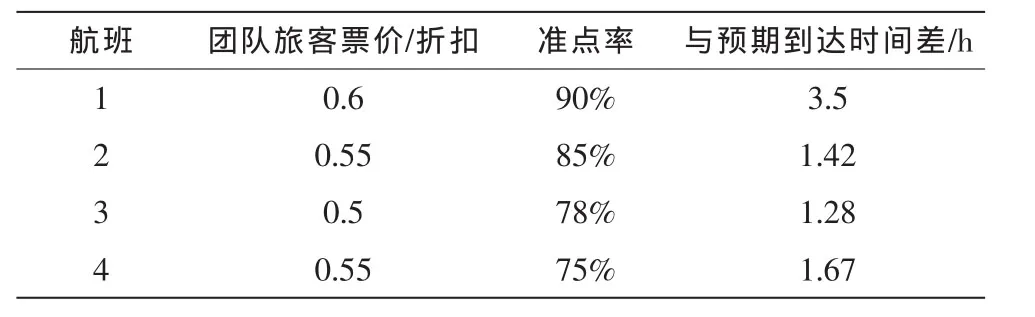
表2 影响旅行代理分配方案的因素Tab.2 Factors influencing the travel agency’s acceptance to group passenger distribution

标准化后的特征矩阵为：

熵 H=[0.846 0.864 0.883]，各影响因素熵权 W=[0.326 0.333 0.341]，进而得综合评分B=[0.635 0.63 0.381 0.335]。通过用maple软件编程得计算结果：

上层规划：最优解U=[1 1 0 0]，最优值F=89.7

下层规划：最优解N=[18 27 0 0]，最优值 f=145.34

由结果可以看出综合得分较低的航班3没有分配到团体旅客，虽然其折扣比较低，与预期达到时间差也较小，4航班也没有分配到团体旅客，这是其准点率较低的缘故。

6 结 论

提出利用双层规划模型对团队旅客进行拆团，上层规划以航线上航班总收益最大为目标，下层以旅行代理接受拆团方案为目标，使得航空公司在增加收益的同时又不会失去旅行代理商。其中下层规划中影响旅行代理接受拆团方案的因素用综合评分得以体现，采用基于熵权法对影响旅行代理决策的因素进行评价，先计算出各影响因素的权重，乘以标准判断矩阵得出各旅行代理对拆团方案的接受度。最后，设计了双层迭代算法求解模型，并结合实例验证了模型和算法的有效性。

[1]高强.航空收益管理中舱位控制问题的研究 [D].南京：南京航空航天大学，2006.

[2]高荣环，许莉.团队旅客收益管理研究[D].南京：南京航空航天大学硕士学位论文，2010.

[3]梅虎，朱金福，汪侠.基于旅客舱位选择的航空收益管理[J].系统工程，2006（9）:25-30.MEI Hu，ZHU Jin-fu，WANG Xia.Revenue management based on passenger seat choice behavior[J].Systems Engineering，2006（9）:25-30.

[4]姚韵，朱金福.基于可拓权重的航班延误服务旅客满意度多级模糊评价模型[J].商业研究，2007（7）:90-125.YAO Yun，ZHU Jin-fu.Based on extension weight flight service passenger satisfaction multi-step fuzzy assessment model[J].Commerce Study，2007（7）:90-125.

[5]王旭，葛显龙，林云.供应商选择的双层规划模型及求解分析[J].计算机工程与应用，2009，45（23）：11-14.WANG Xu，GE Xian-long，LIN Yun.Bi-level programming mode l and solutions analysis for supplier selection[J].Computer Engineering and Applications，2009，45（23）：11-14.

[6]Weber C A，Currint J R.A multi objective approach to vendor selec-tion[J].European Journal of Operational Research，2003，68（2）：73-84.