RC桥式振荡电路性能研究与仿真

吕红娟

（西安铁路职业技术学院，陕西 西安 710014）

正弦波发生电路是在放大电路的基础上加正反馈形成的，其电路种类繁多。正弦波振荡器广泛用于无线通信、测量技术、电子工程和工业生产中[1]，它是各类信号发生器和信号源的核心电路。在此类应用中，对振荡器提出的要求是振荡频率和振荡振幅的准确性和稳定性[2]。笔者着重分析RC桥式振荡器产生稳定正弦输出的条件及频率稳定的有关因素，并基于仿真软件Multisim对其仿真、验证，提出改进方案，具有一定的实用价值。

1 RC桥式振荡电路结构分析

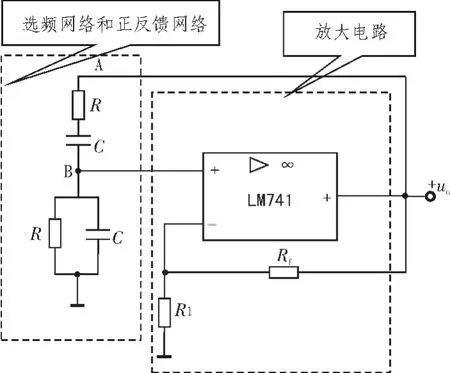
图1 RC桥式振荡电路Fig.1 RC bridge oscillator circuit

基本的RC桥式振荡电路是由放大电路、正反馈和选频网络组成，电路结构如图1所示。

电路中，R和C组成的选频网络兼做正反馈网络。放大器的输出电压作为RC选频网络A点的输入电压，而将选频网络B点的输出电压作为放大器同相端输入电压。

放大器放大倍数Au=1+RfR1。根据起振条件Au＞3可知，只要 Au＞2R1，电路即可起振[1－3]。

RC串并联网络及负反馈电路中的Rf、R1正好构成文氏电桥四臂，如图2所示，所以叫RC桥式振荡器[4]。

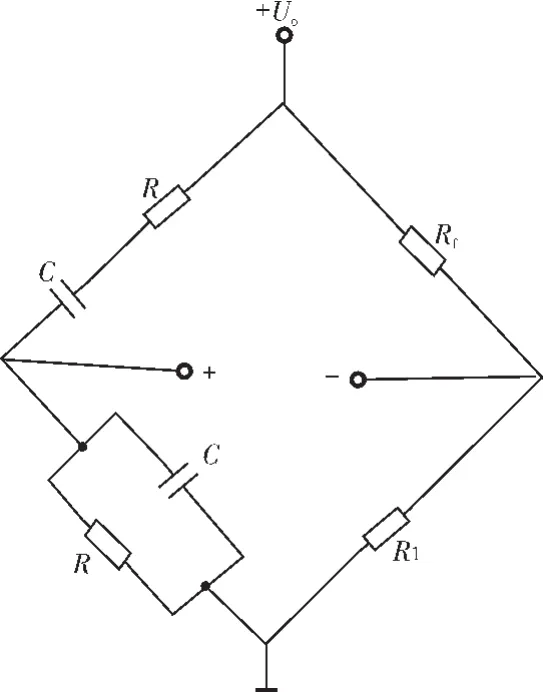
图2 文氏电桥Fig.2 Wen’s bridge

2 RC桥式振荡电路性能分析及改进

2.1 选频网络性能分析

图3为RC桥式振荡电路的选频网络，是一个由两个相同的电阻R和两个相同的电容C组成的一个RC串并联电路。

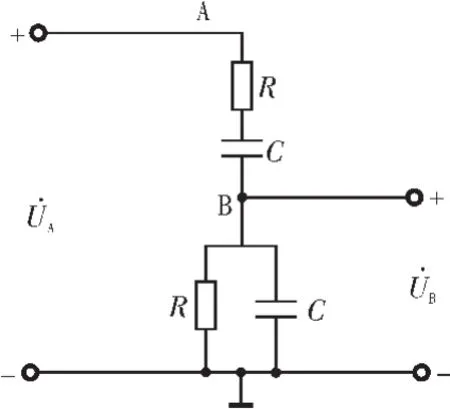
图3 RC串并联电路Fig.3 RC series-parallel circuit

仿真电路和波形如图4所示。电路中R=10 kΩ，C=10 nF，则通过计算

通过调节输入端U˙A信号的频率可看出，只有当输入信号的频率为1.59 kHz时，输入、输出信号相位相同，且输出幅度最大，当输入信号频率大于或小于1.59 kHz时，则输出信号的幅度会马上减小，相位发生偏移[1-2]。

即只有当频率为f0的信号才能通过该选频网络形成正反馈，从而使振荡电路起振。

2.2 稳幅电路设计

对图1所示的振荡电路，当该电路起振后，其输出信号和反馈信号会越来越大，使放大器进入非线性工作区，输出波形就会失真，仿真电路如图5所示[5]。

在仿真电路中Au=1+RfR1=3.1，刚刚满足起振的条件，但输出波形却已经失真，因此，电路还需要稳幅环节，以达到电路起振后保持使输出波形幅度稳定且不失真。

加入稳幅电路的RC桥式振荡电路如图6所示。

V1、V2两个二极管反向并联，再与电阻R2并联，串接在负反馈支路中，不论在振荡的正半周或副半周，总有一只二极管处于导通状态[3-6]。

在起振时，由于输出信号幅度小，所以加在二极管上的电压就小，二极管等效电阻变大，则电路的放大倍数变大，使电路起振。

起振后，由于输出信号幅度变大，所以加在二极管上的电压变大，二极管等效电阻变小，则电路的放大倍数变小，这样就起到稳幅的作用。具有稳幅环节的RC桥式振荡仿真电路及波形如图7所示。

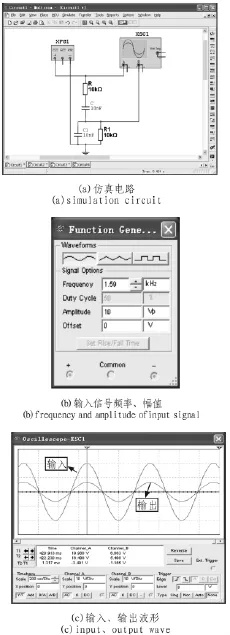
图4 选频网络仿真分析Fig.4 Simulation analysis of frequency network

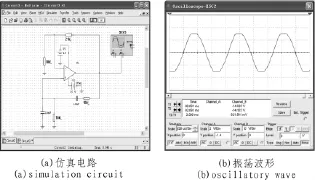
图5 RC振荡电路仿真Fig.5 RC oscillating circuit simulation

2.3 频率可调的RC桥式振荡电路设计

振荡频率连续可调的RC桥式振荡电路选频部分电路如图8所示， 用双层波段开关接不同的电容，作为振荡频率f0的粗调；用同轴电位器实现f0的微调[2]。

图中，如果波段开关选择到C1，则振荡频率：

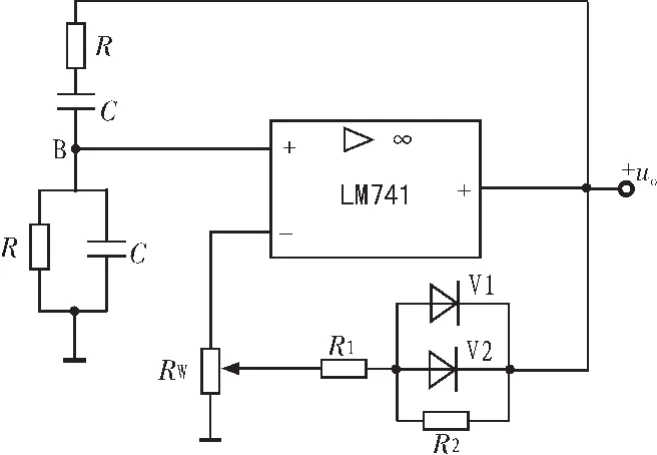
图6 稳幅电路Fig.6 Amplitude stabilization circuit

图7 稳幅电路输出波形仿真Fig.7 Amplitude stabilization circuit output waveform simulation

即当波段开关选择到C1，则振荡频率可在（16.6～265.4 kHz）范围连续可调。

当波段开关选择到C2，则振荡频率可在（1.66～26.5 kHz）范围连续可调。

当波段开关选择到 C3，则振荡频率可在（166 Hz～2.65 kHz）范围连续可调。

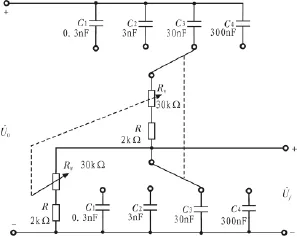
图8 振荡频率连续可调的RC串并联选频网络Fig.8 Oscillation frequency adjustable RC series parallel frequency selection network

当波段开关选择到 C4，则振荡频率可在（17～265 Hz）范围连续可调。

以图8作为振荡电路的选频网络，则可以得到一个频率在17 Hz～265.4 kHz之间连续可调的正弦波振荡器。

3 结 论

RC桥式正弦波振荡电路以RC串并联网络为选频网络和正反馈网络，以电压串联负反馈放大电路为放大环节，具有振荡频率稳定、调节方便，带负载能力强，输出电压失真小等优点，可以在低频的信号发生器等设备中广泛应用。

[1]周雪.模拟电子技术基础[M].西安：电子科技大学出版社，2006.

[2]刘国巍.模拟电子技术基础[M].长沙：国防科技大学出版社，2009.

[3]邹学玉.RC文氏桥振荡器稳幅环节的仿真研究[J].长江大学学报：自然科学版，2011（8）：91－92.ZOU Xue-yu.Simulation on amplitude stabilization circuit for RC wien bridge oscillator[J].Journal of Yangtze University:Natural Science Edition，2011（6）：91－92.

[4]朱晓红.模拟电子电路[M].北京：机械工业出版社，2007.

[5]吴凌燕.基于Multisim 10的正弦波振荡电路仿真 [J].国外电子测量技术，2011（7）:75－76.WU Ling-yan.Circuit simulation of sine wave oscillating based on Multisim 10[J].Foreign Electronic Measurement Technology，2011（7）：75－76.

[6]黄永定.电子线路实验与课程设计[M].北京：机械工业出版社，2005.