一种基于对比度阈值的改进SIFT算法

徐 阳， 曹 杰

（1.南京航空航天大学 电子信息工程学院，江苏 南京 210016；2.南京航空航天大学 无人机研究院，江苏 南京 210016）

近些年来，随着国民经济的发展，无人机遥感技术在城市规划、地理测绘、环境监测、国土资源勘探、军事侦察以及考古等许多领域中发挥着越来越重要的作用。但由于无人机摄像设备的性能以及其它因素的限制，一般只能得到部分区域的图像序列，这就需要通过图像拼接技术将这些图像序列合成一幅大的全景图。SIFT算法[1-2]作为目前图像匹配领域内最活跃的算法之一，对于图像的缩放、平移和旋转都具有良好的不变性，对于光照变化和仿射变换或者三维投影也具有一定的鲁棒性，因此SIFT算法获得了广泛的应用[3-8]。

随着图像的对比度降低，SIFT算法所能提取的特征点数目会大大减少。而在实际的无人机成像过程中，受周围环境因素影响较大，例如由于光照不均匀或者目标本身的灰度特性都有可能造成图像对比度的降低。

在SIFT算法中，剔除对比度小于给定阈值（SIFT推荐为0.03）的特征点，认为这些点是不稳定的，但固定的阈值无法适应图像对比度的变化，同时会造成图像局部范围内特征点的分布不均。一种解决方法是将原始图像进行对比度增强，然后对其进行SIFT特征提取。但是对比度增强是一种有损处理，对图像的质量会造成损害，影响配准精度。另一种方法是根据图像的对比度人工调整阈值，但人工调整阈值无法适应图像自动配准的要求，大大增加了工作量，不符合实际工作需求。另外，在图像匹配的实际应用中，SIFT算法可能会提取出数千甚至上万的特征点，这对于图像匹配而言毫无必要，反而大大的延长了算法运行时间，增加了工作量。

1 SIFT算子简介

1.1 尺度空间的建立和尺度空间特征点检测

高斯卷积核是实现尺度变换的唯一线性核，因此，一幅二维图像的尺度空间L（x，y，σ）定义为该图像与高斯尺度函数的卷积，即：

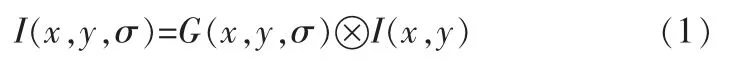
其中，G（x，y，σ）是尺度可变的高斯函数，⊗表示卷积，I（x，y）表示输入图像，（x，y）表示图像像素的位置，σ是尺度因子。

为了有效检测出稳定的特征点，Lowe于1999年提出了高斯差分尺度空间（DoG，Scale－ space，Difference of Gaussian Scale－space），即两个不同尺度的高斯差分核与图像进行卷积构成的空间。DoG算子D（x，y，σ）通过将相邻的高斯尺度函数与图像卷积后作差得到，即：

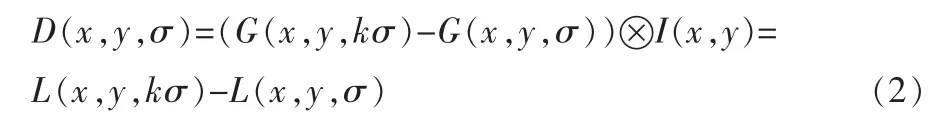
式中，k为每两个相邻尺度之间的相隔线型比例因子，k=21/s。

1.2 精确定位特征点

特征点的位置和尺度是通过三维二次函数拟合来完成的，同时去除了对比度比较低的候选特征点和不稳定的边缘响应点（DoG算子产生的较强的边缘响应），从而增强了匹配的稳定性、提高了算法的抗噪性。差分

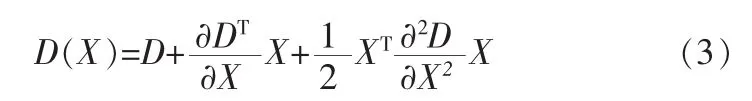
其中 X=（x，y，σ）T为包含特征点位置和尺度信息的响亮。有由差分金字塔DoG的幅值大小及曲率来剔除低对比对点和边缘响应点。

1.3 特征点主方向的确定

坐标的关键点，其梯度幅值和方向分别为：

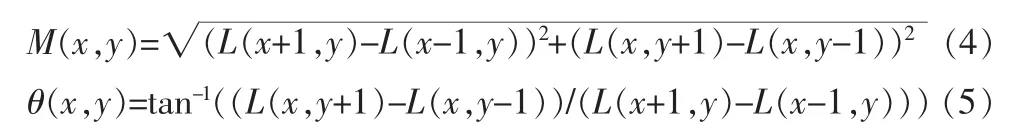
在以特征点为中心的邻域窗口内使用梯度方向直方图统计邻域像素的梯度方向。梯度方向分布在0°～360°，其中在直方图中每10°表示一个柱，共计36柱。梯度方向直方图的峰值代表了该特征点处邻域梯度的主方向。

1.4 特征点描述子的生成

以特征点作为中心取16×16的窗口。每个小格表示特征点邻域所在尺度空间的一个像素。通过高斯加权在4×4的图像小快上计算8个方向上的梯度直方图。绘制各梯度方向的累加值，形成种子点。梯度方向直方图统计公式如下：

其中，ck为柱中心，Δk 为柱的宽度。 （x，y）为子块 r（l，m）像素点坐标。

每个特征点由个种子点组成。特征描述子由所有子块的梯度方向直方图构成。最终形成128维的SIFT特征向量。

2 改进的SIFT算子

2.1 SIFT算子对比度阈值的分析

由上一部分内容可知：SIFT算法在DoG尺度空间检测极值，得到候选特征点集。如图1所示，检测极值时，图1中标记叉号的像素要和包括同一尺度空间的周围8个像素以及相邻尺度空间周围邻域9×2个像素共计26个像素进行比较，以检测到局部极值。之后通过拟合三维二次函数去除低对比度的关键点和边缘响应点。

因此在SIFT特征检测时包含两个参数，分别是对比度阈值和曲率阈值。通过这两个阈值对SIFT初始特征点进行筛选。本文中主要讨论对比度阈值对结果产生的影响，故曲率阈值取 10（SIFT 推荐）。 图 2（a）、图 2（b）和图 2（c）分别为同一场景不同对比度下的照片。 图 2（a）、图 2（b）和图 2（c）检测到的SIFT初始特征点数目分别为16456、16895和16926。这表明算子检测特征点的能力不会随着图像对比度的变化而变化。此时，令对比度阈值等于0.03对初始特征点进行过滤，得到的特征点数目分别为 3693、1958和 855，分别如图 3（a）、图3（b）和图3（c）所示。由此可见，图像对比度越低，对比度阈值对于关键点数目影响越大。因此，SIFT算法中的对比度阈值应根据图像的不同，设置为不同的值，这样才能保证SIFT算法检测能力的鲁棒性。

图2 同一场景不同对比度下的照片Fig.2 Images in the same scene under different contrast

图3 特征点数目截图Fig.3 Number of feature points

2.2 自适应对比度阈值的确定

根据式（2）知，k值越小，金字塔层数越多，相邻的上下层高斯图像的差值越小，DoG尺度空间中的极值就越小；除此，若图像的灰度分布越集中，DoG图层取值范围就越小，导致极值越小。这说明，DoG尺度空间的灰度信息反映了极值的变化范围，所以以特征点为中心的DoG图层的局部邻域反映了极值的变化范围。因此本文根据图像DoG尺度空间局部邻域的灰度信息，来确定对比度阈值。取以候选SIFT特征点为中心的9×9区域为邻域，计算该邻域内所有像素灰度绝对值的均值，记为δ。我们取kδ作为改进后SIFT算法的对比度阈值。

通过分析发现，SIFT算法的计算时间主要耗费在检测极值点和描述特征向量这两个步骤。对于自适应对比度的系数k的值，若过大，则可能无法提取到足够的特征点；若过小，提取出的特征点过多，提取出匹配点对于图像变化矩阵H的确定远远足够，反而只会使算法计算量变大，效率降低。据此，本文提出可变的自适应对比度阈值系数。具体调整方法如下：

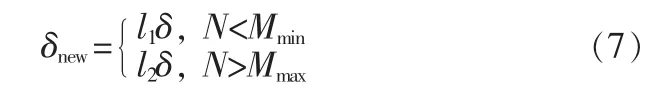
其中δnew为新的阈值，δ为自适应对比度阈值，l1和l2为阈值调整系数。设N为即时检测出的特征点数目，Mmin和Mmax为预先设定的特征点数量区间。当N＜Mmax时，需减小阈值以获得更多的特征点，根据经验值，将l1设为1.3；反之，若N＞Mmax，将l2设为10。具体步骤如下：

1）首先设置特征点数量区间。应确保可以计算出正确的图像变换矩阵，又可避免过多运算。一般情况下，设置Mmin=1 200、Mmax=1 700可以取得较好结果。

2）计算待匹配图像即时的特征点数量。在初始阈值或者步骤4产生的新阈值下计算待匹配图像的特征点。

3）判断特征点数量是否满足要求。若其在预定的区间内，进行步骤5的计算过程。否则生成新的阈值继续计算。

4）生成新阈值。按照式（7）生成新的阈值。根据新阈值大小分为两种情况：当阈值降低时，需重新进行待匹配图像特征点检测；反之，阈值升高时，直接判断特征点数量是否满足要求。

5）进行图像匹配其他步骤。使用以上步骤返回的阈值进行其他SIFT算法步骤。

综上，采取具有动态系数的自适应对比度阈值δnew，既可以在处理低对比度图片时提取到足够多的特征点，又可以有效地控制特征点数目，大大优化了算法运算量，提高了算法的效率。

3 实验结果及讨论

此实验的目的在于比较本文算法和传统的固定对比度阈值SIFT算法提取特征点的能力和效率。文中通过大量实验，但由于篇幅限制下面只选取其中两张详细说明。如图4所示。

图4 相同场景不同对比度下的图片Fig.4 Images in the same scene under different contrast

图4（a）和图4（b）为相同的场景在不同对比度下的图片，其中图4（b）的对比度极低。

图5（a）为采用固定阈值SIFT算法（对比度阈值取0.03）对图4（a）进行特征提取的结果，共计提取5 011个特征点，耗时25.092 s；图4（b）采用固定阈值SIFT算法没有提取到特征点。图 5（b）和图 5（c）为采用本文算法对图 4（a）、图 4（b）分别提取特征点的结果，图4（a）共计提取1 791个特征点，耗时 11.996 s；图 4（b）共计提取到 1 737 个特征点，耗时 11.545 s。如下表所示：

通过比较，明显可见：1）改进后的SIFT算法相比原来的SIFT算法提取特征点的能力显著增强，即使对于对比度很低的图像，也能提取到足够的特征点，并且提取的特征点均匀分布于整个图像。2）改进后的SIFT算法相比原来的SIFT算法节省了超过一半的时间，算法效率提高了一倍多。

4 结 论

图5 不同算法下的特征点截图Fig.5 Figures of the feature points in the different algorithms

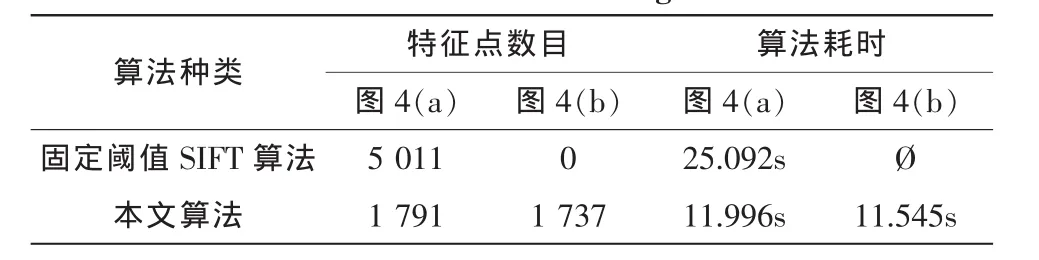
表1 两种算法处理的结果Tab.1 Test results of two algorithms

文中提出的具有可变系数的自适应对比度阈值SIFT改进算法，改进后的算法不仅增强了对于图像对比度变化的鲁棒性，而且大大提高了算法的效率。该实验结果表明在图像对比度较低时，可以提取到足够多的特征点用于特征匹配，并且改进后的算法提取到的特征点分布非常均匀，能够有效地提高图像配准的精度；另外，改进后算法可以有助于避免提取过多的不必要的特征点，大幅度的提高了算法的效率。该算法无须根据图像不同，人工调整SIFT对比度阈值，非常适合需要使用自动匹配的场合。

[1]LOWE D.Object recognition from local scale-invariant features [C]//Proceeding of ICCV Piscataway，NJ，USA:Institute of E-lectrical and Electronics Engineers Inc，1999:1150-1157.

[2]LOWE D.Distinctive image features from scale-invariant key-point[J].International Journal of Computer Vision，2004，60（2）:91-110.

[3]Stereo Cameras Self-calibration Based on SIFT[C]//proceedings of the International Conference on Measuring Technology and Mechatronics Automation，2009:352-355.

[4]伯将军，郭书军，伍淳华.SIFT局部特征描述算法在图像版权搜索中的应用[J].电子设计工程，2012，20（3）:137-141.BO Jiang-jun，GUO Shu-jun，WU Chun-hua.Application of SIFT algorithm in the image copyright search[J].Electronic Design Engineering，2012，20（3）:137-141.

[5]孙艳丽，李建海，周伟，等.SIFT在高分辨率SAR图像自动配准中的性能分析[J].电子设计工程，2011，19（7）:180-183.SUN Yan-li，LI Jian-hai，ZHOU Wei，et al.Performance analysis of SIFT to registration of high-resolution accuracy SAR imagery[J].Electronic Design Engineering，2011，19（7）:180-183.

[6]张建花，白仲斐，惠广裕.基于SIFT算法的异源遥感影像自动匹配研究[J].电子设计工程，2011，19（13）:176-179.ZHANG Jian-hua，BAI Zhong-fei，HUI Guang-yu.Research on automatic registration of multi-source remote sensing images based on SIFT algorithm[J].Electronic Design Engineering，2011，19（13）:176-179.

[7]徐昱琳，张雷，陈万米，等.基于SIFT特征和图割算法的图像分割方法研究[J].计算机测量与控制，2009，17（12）:2491-2499.XU Yu-lin，ZHANG Lei，CHEN Wan-mi，et al.Image segmentation based on SIFT feature and graph cuts[J].Computer Measurement&Control，2009，17（12）:2491-2499.

[8]李晓明，郑链，胡占义.基于SIFT特征的遥感影像自动配准[J].遥感学报，2006，10（6）:885-892.LI Xiao-ming，ZHENG Lian，HU Zhan-yi.SIFT based automatic registration of remotely-sensed imagery[J].Journal of Remote Sensing，2006，10（6）:885-892.