遗传模糊优化算法在三容水箱控制系统中的仿真应用

冯鹏辉, 谭 兮, 刘国营, 彭传伟

(湖南工业大学 电气与信息工程学院, 湖南 株洲, 412008)

遗传模糊优化算法在三容水箱控制系统中的仿真应用

冯鹏辉, 谭 兮, 刘国营, 彭传伟

(湖南工业大学 电气与信息工程学院, 湖南 株洲, 412008)

针对存在大滞后、时变、非线性特点的液位控制系统在工况大范围变化时传统控制算法控制效果不理想的问题, 提出利用模糊控制结合遗传算法的空间寻优能力, 对隶属度函数的参数和模糊控制规则的后件进行综合编码优化, 利用进化原理寻优来获得最佳的参数进行模糊系统自动设计的方法建立三容水箱控制系统仿真模型,在此模型上验证. 仿真结果表明此方法的有效性和实用性.

三容水箱; 液位控制; 模糊控制; 遗传算法

液位是生产生活中常见且重要的物理量, 在许多生产过程中都需要对液位进行检测和控制, 以保证生产正常连续运行, 确保产品质量.

三容水箱液位控制系统是工业生产过程中多容流量对象的抽象模型, 具较强的代表性, 可模拟工业生产过程中一阶或多阶次、线性或非线性、单容或多容、耦合或非耦合等特性, 以判别或验证各种控制策略性能的优劣. 因此, 对三容水箱的控制系统进行研究有重要的理论意义和实际应用价值.

目前对三容水箱控制策略的研究主要集中在以下方面[1-2]: a)先进PID控制. 将传统PID与各种智能算法结合起来, 取长补短. b)模糊控制. 提出了一种新的机制用于实现基于知识(规则)甚至语义描述的控制规律为非线性控制器提出了一个比较容易的设计方法. c)神经网络控制. 利用神经网络自学习和自适应的特点构成控制器. d)预测控制. 基于前馈补偿解耦的预测函数算法应用于三容水箱控制. e)无模型自适应控制.利用新引入的伪梯度向量和伪阶数的概念, 在受控系统轨线附近用一系列的动态线性时变模型来替代一般非线性系统. f)动态矩阵控制. g)智能复合控制. 将各种智能算法结合, 构成新型控制器.分析以上控制策略的优缺点, 提出利用模糊控制结合遗传算法的空间寻优能力, 对隶属度函数的参数和模糊控制规则的后件进行综合编码优化, 利用进化原理寻优来获得最佳的参数, 进行模糊系统自动设计的方法, 为模糊系统建模提供了很好的途径, 最后利用MATLAB建立模型进行仿真实验验证, 结果表明此方法具有较高的自适应性和鲁棒性.

1 液位控制系统结构及数学模型

三容水箱控制对象的模型[3]如图1. 对图1所示模型进行数学分析, 可得该系统的动态方程[3]为:

图1 三容水箱实验模型

式(1)中: C1、C2和C3分别为3个水箱的液容, 且C1= C3= 166 585 mm3, C2= 169 510 mm3; f1(h1), f2(h2), f3(h3)分别为3个水箱的出水流量, 由所设置的阻力板流量特性决定.

对单个水箱进行分析, 取过阻力板底边的直线为x轴, 过底边的中点垂直向上为z轴. 非线性阻力板结构如图2所示.

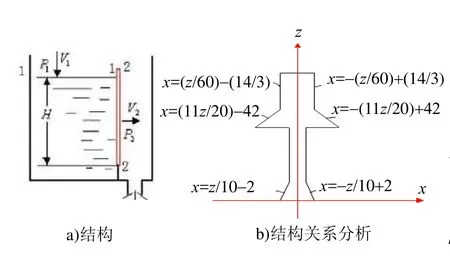
图2 非线性阻力板结构

对图2所示模型建立直角坐标系, 实际液位高度为h, 取 z为积分变量, 它的变化区间为[0, h], 采用定积分元素法可求得水箱不同液位高度h时流过阻力板的液体流量Q. 其计算式为. 积分可得:

由于实际的液体有黏性, 在流动过程中必然有能量损失, 因此实际流量比理想流量值要小, 所以进行流量计算时, 需加入修正系数β. 经过试验测得流量系统β可近似表示为:

根据以上分析, 我们可以利用合M函数编写三容水箱控制系统仿真模型. 其中, 进水阀门最大比例度对应流量Qmax, 其值为233 219 mm3/s.

2 模糊控制系统的设计

2.1 控制器的结构

模糊控制系统由模糊控制器和控制对象组成, 如图 3所示. 模糊控制器的基本结构见图 3虚线框中. 模糊控制器主要由4部分组成: 模糊化、模糊推理、清晰化和知识库. 针对本系统模糊控制器采用两个输入E、EC, 一个输出U;

2.2.1 模糊化

a) 论域的定义

对误差E、误差变化率EC和控制量U的模糊集定义如下: E、EC、U的模糊集均为: {NB, NM, NS, ZO, PS, PM, PB}, E 和EC的论域为[-6, 6], U的论域为[0, 12].

b) 尺度变换

尺度变换的定义: 变量的实际区间和论域区间的映射.在本论文中, 对于连个输入量E和EC采用线性变换, kE= 0.25, kEC= 0.3. 输出量 u, 由于水箱稳态时阀开度与三号水箱液位高度之间的非线性, 因此通过人工取点计算稳态时, 阀开度与三号水箱的液位高度关系, 通过去多组数值拟合来得到 kU曲线. 如表1, 拟合后见图4.

图3 模糊控制器结构

图4 调整因子ku拟合曲线

表1 静态水位/开度对应表

c) 隶属度函数

采用B样条隶属度函数(B-spline members function), 其数学表达式为:

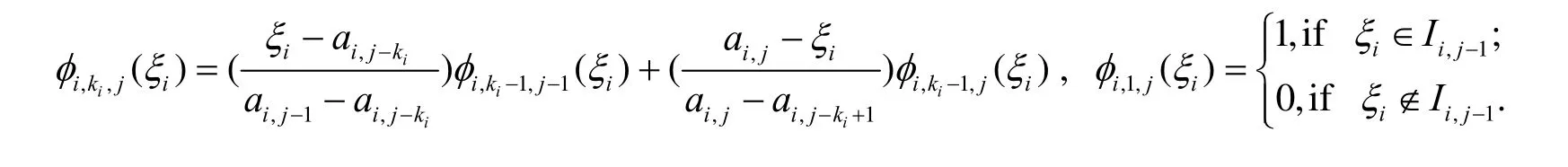
图5 B样条隶属函数

B样条函数[5]是一个简单的分段多项式映射, 其主要参数为一组“节点向量”, 即图中[a1, a2, a3, a4]. 图5是误差E的隶属函数, 误差的变化EC以及控制量U的隶属函数与图5类似, 其节点向量可分别设为[a5, a6, a7, a8]和[a9, a10, a11, a12].

2.2.2 模糊规则设计

获取模糊规则的方法[4-5]主要有 3种: 方法一: 基于控制工程知识和专家经验; 方法二: 基于手工控制操作的系统观察和测量; 方法三: 基于学习算法; 前两种方法均依赖于实际工作人员的经验, 规则的获取存在很大的不确定性; 第三种方法将模糊控制与目前的智能研究相结合, 利用其自学习能力自动获取规则.在本文中, 提出利用遗传算法的自寻优能力, 来获取模糊规则以及优化隶属函数.

在本论文中, 因为确定了模糊控制器的输入输出变量的模糊集均为{NB, NM, NS, ZO, PS, PM, PB}. 模糊规则表现形如“if E is P and EC is Q,then U is M”,其中P、Q、M均为模糊集合中的元素. 在此, 对模糊规则的后件即M∈{NB, NM, NS, ZO, PS, PM, PB}进行编码, 与前面的隶属度函数参数一起进行遗传算法寻优, 从而确定出模糊规则.

2.2.3 模糊推理和清晰化

模糊推理和清晰化的方法很多, 在本论文中, 采用的是Mamdani推理方法, 推理规则为:

3 遗传算法

遗传算法实现的基本步骤[6-7]如下: a) 初始化种群; b) 计算种群中每个个体的适应度值; c) 按由个体适应度值所决定的某个规则选择将进入下一代的个体; d) 概率进行交叉操作; e) 按概率进行变异操作; f) 若没有满足条件, 则转第 b)步, 否则进入下一步; g) 输出群体中适应度值最有的染色体作为问题的满意解或最优解.

3.1 遗传算法的计算机实现

本论文利用MATLAB软件编制了遗传算法程序, 对模糊控制参数进行寻优. 以上流程中各步骤的具体编码实现.

a) 参数初始化

遗传算法的运行依赖于各种参数, 主要有种群规模N、交叉概率Pc、变异概率Pm和终止进化代数T. 本论文中, 设定N = 80, Pc= 0.9, Pm= 0.03, T = 30.

b) 初始种群的生成

遗传算法所能处理的是数字串, 因此待优化的参数需经过变换才能成为种群中的个体. 本文采用的是二进制编码(binary encoding), 即个体是二进制字符串. 编码的长度由参数的精度决定.. 其中, ai、bi是某参数xi取值的下边界和上边界, mi是该参数编码的长度, ε是编码的精度. 本文的优化变量分为两部分: 第一部分是模糊控制器的隶属函数, 其参数节点向量为[a1, a2, a3, a4]、[a5, a6, a7, a8]和[a9, a10, a11, a12]. a1～a8的取值范围为[-6, 6], a9～a12的取值范围为[0, 12]. 在编码时, 统一取值范围设定为[-6, 6], 最后对a9～a12依次加上6, 使其重新映射为[0, 12]. 依上式的mi= 5. 则个体的第一部分编码长度为L1= 12×5 = 60.第二部分是模糊规则的后件M∈{NB, NM, NS, ZO, PS, PM, PB}. 采用三位二进制数即可表示U(i, j). L2= 49 ×3 = 147. 将两部分结合, 个体的编码长度为L = L1+L2= 195.

c) 适应度函数

为了获取满意的过渡过程动态特性, 采用误差绝对值积分[3]性能指标作为参数选择的最小目标函数.

式中, e(t)为系统误差, u(t)为系统输出, tu为上升时间, w1, w2, w3为权值. 为了避免超调, 采用了罚函数项, 即一旦产生超调, 将超调量作为最有指标的一项, 此时最优指标为:

d) 选择算子

选择算子(selection operator)是决定父代中那些个体、能以多大的可能性被挑选来复制或遗传到下一代的进化操作. 本文采用轮转法进行选择操作, 此方法可以使每个个体都有均等的概率参与选择操作.

e) 交叉算子

交叉算子的基本操作是从一对父代染色体中生成一个或者多个新的个体. 本文中采用单点交叉, 等概率随机指定一个基因位置作为交叉点, 再把两个父代个体从交叉点分为前后两个部分, 以某个确定概率交换两个个体的后半部分.

f) 变异算子

变异操作独立分别作用于种群中的每个个体的每一个基因, 以某一概率产生成变异, 从而抑制优化过程陷入局部最优.

g) 解码

解码是编码过程的逆运算, 即将个体由二进制字符串变化为待优化的隶属度函数和模糊控制规则的后件.

4 控制器的仿真

本论文采用三容水箱作为控制对象, 利用模糊控制器来控制阀门的开度, 从而来达到对三号水箱液位的良好控制. 本文程序均采有M函数编写, 仿真过程如图6.

图6 程序结构

水位设定为30 cm时的一段寻优过程如图7和图8所示.

图7 代价函数J的优化过程

图8 二进制遗传模糊优化算法的阶跃响应

遗传模糊优化算法寻优获得的最优控制规则如表2:

表2 模糊控制规则表

由图 9所示仿真控制过程曲线可看出, 利用遗传算法寻优模糊控制参数的方法, 系统的调整时间均在300 s以下, 最大超调量低于 3%, 无静差. 这一结果表明, 利用遗传算法对模糊控制器隶属度函数参数及规则同时寻优的方法, 能够大大提高控制品质, 具有较好的自适应性、鲁棒性.

图9 连续过程仿真

5 结语

模糊系统的最显著缺陷就是依赖工作人员的经验和专家知识, 缺乏有效的学习机制, 本文将遗传算法的进化功能应用于模糊系统的结构学习上, 研究在没有数据分布的任何先验信息的情况下, 如何依靠遗传算法全局搜素获得最优系统解, 使其解决了对工作人员的经验和专家知识的依赖, 自动设计模糊控制器.最后通过建立三容水箱的控制模型, 检验其可行性及有效性, 仿真实验表明遗传算法与模糊控制的结合具有非常好的自适应性和鲁棒性.

[1] 张波. 动态参数调整遗传模糊优化算法及在机器人轨迹控制中的应用[D]. 长沙: 湖南大学, 2008: 22-36.

[2] Zhang bo. The fuzzy control optimized by the dynamic parameter adjustment genetic algorithm and its application in robot trajectory control[D]. Changsha: Hunan University, 2008: 22-36.

[3] 赵科, 王生铁, 张计科. 三容水箱的机理建模[J]. 控制工程, 2006, 13(6): 521-524.

[4] 刘金琨. 先进PID控制及其MATLAB仿真[M]. 北京:电子工业出版社, 2003: 115-129.

[5] 张国良, 曾静, 柯熙政, 等. 模糊控制及其MATLAB应用[M]. 西安: 西安交通大学出版社, 2002: 69-84.

[6] 张林伟. 基于遗传算法的模糊控制系统的研究[D]. 长春: 长春理工大学, 2005: 32-37.

[7] 雷英杰, 张善文, 李续武等. MATLAB 遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2005: 34-61.

(责任编校： 刘刚毅)

Fuzzy optimization based on genetic algorithm in simulation application of three-tank liquid level control system

FENG Peng-hui, TAN Xi, LIU Guo-ying, PENG Chuan-wei
(School of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412008, China)

According to the problem of the existence of large time delay, time-varying, non-linear characteristics of liquid level control system in the condition of changes in a wide range, the traditional control algorithm control is not ideal, a new control method combining fuzzy control combined with the ability of optimization of Genetic Algorithms to auto-design of Fuzzy Systems is proposed, and genetic Algorithms is used to encode and optimize the parameters of membership functions and the consequents of fuzzy rules by evolutionary theory to get the best parameters, and the simulation model of three-tank liquid level control system is established based on the simulating result verifies. The method is effective and practical.

three-tank; level control; fuzzy control; genetic algorithm

TH 122; TH 137.52

1672-6146(2012)02-0046-05

10.3969/j.issn.1672-6146.2012.02.012

2012-05-03

冯鹏辉(1988-), 男, 硕士生, 主要研究方向为智能控制、交流调速. E-mail: fph136295446@163.com