一种新的QAM信号信噪比估计算法

韩 博，吴 杰，许 华，李 鹏

(空军工程大学电讯工程学院，陕西 西安 710077)

信噪比是现代通信系统中一个重要的通信参数，通信链路的功率分配、自适应调制切换以及卫星通信的功率控制所需的有效信道质量信息必须由信噪比提供[1]，许多解调和译码的算法也都需要准确的信噪比信息才能达到最优的性能[2]。目前对于恒模信号信噪比估计的研究已经非常成熟，而且已有很多算法被提出。相比之下，非恒模信号的信噪比估计研究较少，且估计性能不佳。文献[3]总结了在加性高斯白噪声条件下几种经典的信噪比估计方法，但是都仅限于对MPSK信号进行研究;在文献[3]之后出现了较多基于统计量的信噪比估计算法[4－8]，但是针对幅相调制信号的信噪比估计算法较少;文献[9－11]均是基于子空间分解的信噪比估计算法，效果较好，但是都没有解决相关矩阵计算量大的问题。

因为QAM信号是非恒模调相调幅信号，而高阶统计量可以不考虑信号的幅度和相位变化，所以本文通过建立采样信号的二阶和四阶矩与信噪比之间的线性关系，利用最小二乘数据拟合，得到信噪比估计关系式。

1 模型建立

在平坦衰落信道下，假设系统不受均衡和同步的影响。经匹配滤波器且采样后的输出信号为

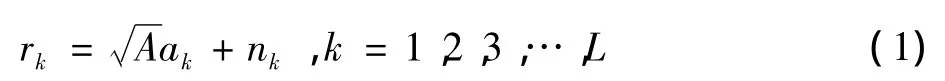
2 算法分析

定义信噪比

根据S和N的定义，联立(3)，(5)，(6)式可得[7]

可以求得信噪比为

若λ单位为dB，可以利用最小二乘进行数据拟合得到多项式

式中，a0～a5为需要拟合的系数。

综上所述，求解信噪比的步骤为:第一步，在得到样本矩M2，M4之后，利用式(11)求得 λ;第二步，利用式(13)得到信噪比ρ。由于各种常用的QAM信号星座分布都不一样，不能利用唯一的系数求得各个信噪比，所以本文将各个QAM信号的系数都列在表1中。

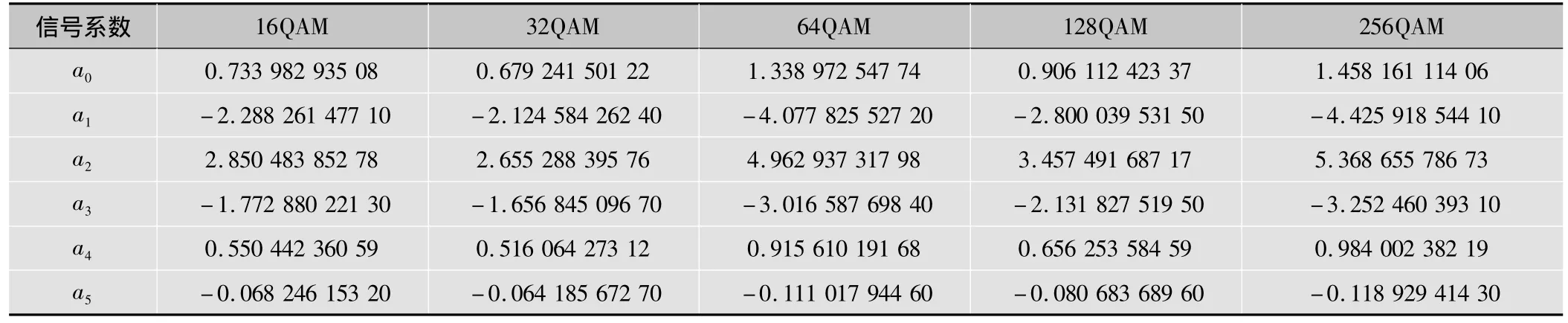
表1 各阶QAM信号拟合系数

3 仿真结果分析

采用蒙特卡罗法对算法进行仿真验证。仿真参数的测试范围为0～20 dB。标准差是方差的平方根，它可以更直观地显示估计性能，所以本文通过对估计标准差的比较来分析新算法的优劣。图1、图2选取16QAM，64QAM和128QAM进行仿真比较。

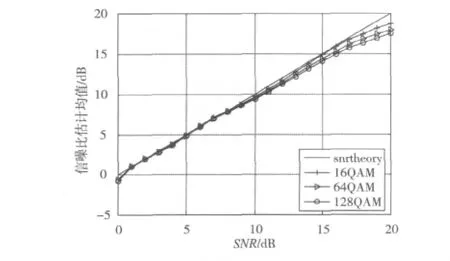
图1 信噪比估计值均值比较(L=5000)

从图1、图2可以看出，当数据长度L=5000时整个信噪比都比较趋近理论值，所以可认为是渐进无偏的。在仿真结果中，3种信号中16QAM效果最好，在相同数据长度下阶数越高效果越差。随着QAM调制阶数的增高，要获得较高的估计精度，所需的数据量也要增加。

为了研究数据长度对算法性能的影响，本文对256QAM在不同数据长度下进行了仿真。

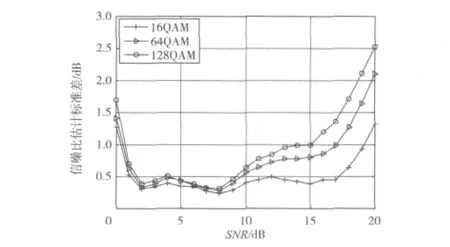
图2 信噪比估计值标准差比较(L=5000)

如图3，随着数据长度的增加，性能逐渐变好，且误差在1 dB内。所以在实际应用中应当综合考虑信噪比估计精度的要求和数据长度的影响，合理进行选择。

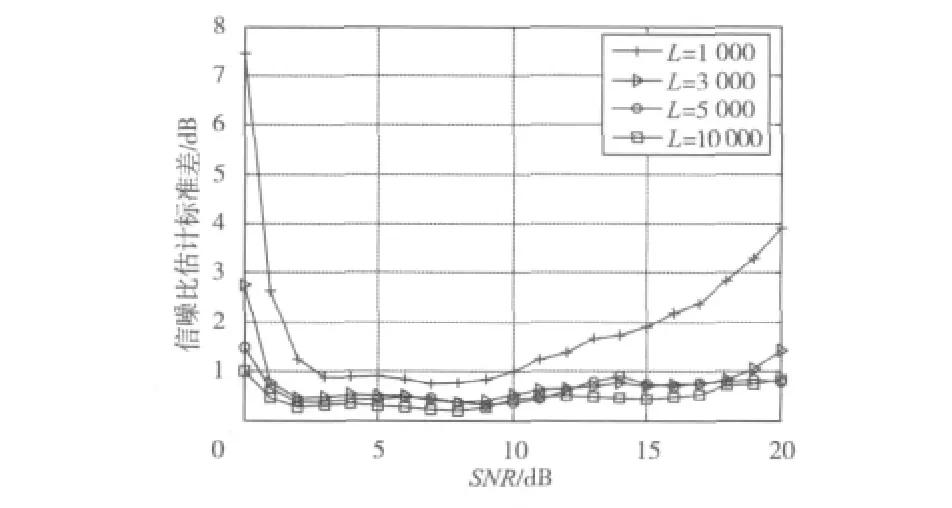
图3 256QAM不同数据长度标准差比较

4 算法复杂度分析

该算法虽然实现简单，且估计精度较高，但是带来了复杂度较高的问题，复杂度为O(5)。在实际应用当中，可以将复杂度降低到O(4)或者O(3)。如针对256QAM的三阶和四阶多项式为

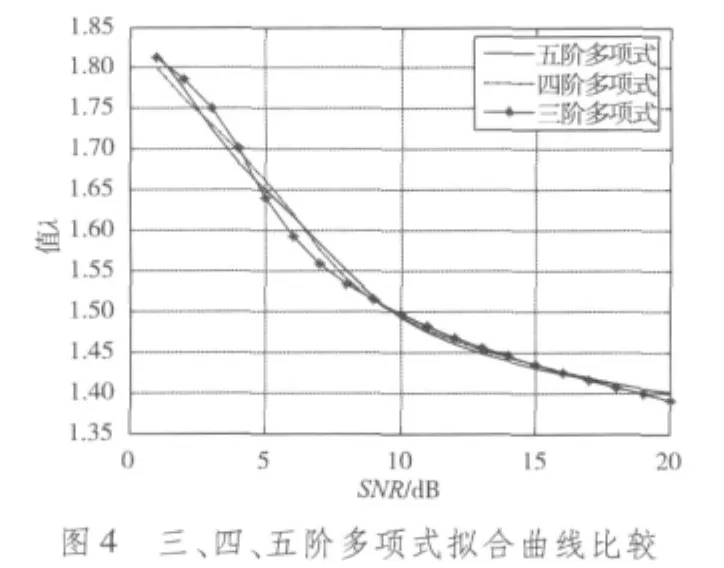
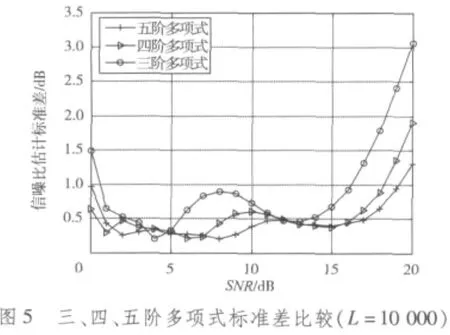
256QAM的三、四、五阶拟合曲线如图4所示，标准差比较如图5所示。在图4中，3种拟合多项式的拟合曲线基本接近，所以拟合程度误差不大，在实际应用中，若对信噪比精度要求不高，可采用阶数较低的多项式进行求解。图5中也能说明改进后的三阶和四阶多项式性能较好，误差在可接受范围内，只是要精确估计时(误差＜1 dB)，三阶多项式估计范围可确定为0～16 dB，四阶估计范围为0～18 dB。

综上所述，本文提出的新算法比较简单，估计范围较大，估计精度较高，尤其是改进后的算法，复杂度明显降低，且实用性更强。

5 小结

本文通过建立起各QAM信号信噪比与统计量二阶、四阶矩之间的线性关系，并利用最小二乘算法，拟合出关系式中的各系数。新算法对于各阶QAM信号均适用，估计精度小于1 dB，在考虑了运算复杂度后，提出了基于低复杂度下的改进算法，改进后的算法降低了复杂度，但是估计范围有所减小，四阶减小到0～18 dB，三阶减小到0～16 dB。

[1]WIESEL A，GOLDBERG J，MESSER H.Non－data－aided signal－tonoise－ratio estimation [C]//Proc.IEEE ICC.[S.l.]:IEEE Press，2002:197－201.

[2]KHALIGHI M A.Effect of mismatch SNR on the performance of log－MAP turbo detector[J].IEEE Trans.Commun，2003，52(5):1386－1397.

[3]PAULUZZI D R，BEAULIEU N C.A comparison of SNR estimation techniques for the AWGN channel[J].IEEE Trans.Commun.，2000，48(10):1681－1691.

[4]BEAULIEU N C，TOMS A S，PAULUZZI D R.Comparison of four SNR estimators for QPSK modulations[J].IEEE Commun.Letters，2000，4(1):43－45.

[5]STéPHENNE A，BELLILI F，AFFES S.Moment－based SNR estimation over linearly－modulated wireless SIMO channels[J].IEEE Trans.Wireless Communications，2010，9(2):714－722.

[6]ZHAO Hongyu，FAN Pingzhi，TAKIS M P，et al .On SNR estimation techniques for Turbo decoding over uncorrelated Rayleigh fading channels with unknown fading parameters[J].IEEE Trans.Vehicular Technology，2009，58(9):4955－4961.

[7]LOPEZ－VALCARCE R，MOSQUERA C.Sixth－order statistics－based non－data－aided SNR estimation[J].IEEE Communications Letters，2007，11(4):351－353.

[8]áLVAREZ－DíAZ M，LóPEZ－VALCARCE R，MOSQUERA C.SNR estimation for multilevel constellations using higher－ order moments[J].IEEE Trans.Signal Processing，2010，58(3):1515－1526.

[9]隋丹，葛临东.一种新的基于改进PA STd的中频信号盲信噪比估计算法[J].电子与信息学报，2007，29(7):1657－1661.

[10]唱亮，汪芙平.非协作通信中的盲信噪比估计[J].通信学报，2008，29(3):76－81.

[11]张金成，彭华.一种鲁棒的基于子空间分解的盲信噪比估计方法[J].数据采集与处理，2011，26(5):609－614.