视觉测量中可纠错编码点的算法研究

田苗苗，杨秋翔，杨 剑，苏承启

(中北大学电子与计算机科学技术学院，山西 太原 030051)

三维视觉测量中，图像匹配是三维重构过程中最关键的一步。通常的三维扫描系统从不同的视角得到物体的一部分点云数据，要得到物体的三维结构，需要对多个点云数据进行拼接。把不同视角拍摄的图片采用相应的技术转换到同一坐标系下，从而得到物体完整的三维形状。

对于点云拼接的技术，大体分为2大类。

第1类技术采用经过高精度定标的仪器获取的多视点数据以及它们之间原始变换关系或引入特征点信息，利用场景中原有的信息进行匹配。这类方法需要改变探头的方向或对被测物体进行重定位，将从不同角度获取的图像转换到同一坐标系下。但是改变探头方向每次拍摄都需要对探头的外参数进行重新标定。这种方法操作复杂，不便于实际应用[1]。如果采用探头方向不变，把物体放到旋转的转台上进行测量，这种方法虽然不需要每次进行探头标定，但是拍摄物体时无法获取物体的头部和底部[2]。这类技术可以概括为2类:基于区域的匹配和基于特征的匹配[3]。基于区域的匹配是在一幅图片像点的相邻区域内利用图片的灰度信息找到另一幅图片相同或相似的灰度进行匹配。这类方法的缺点在于对图像的旋转、缩放、光强以及对比度的变化比较敏感，因此匹配的精度较低，不能用于精确的测量领域。基于特征的匹配由于在不同视角下，特征点之间具有空间特征不变性，采用不同的算法进行匹配，例如松弛算法[4]、动态规划算法[5]、或者尺度不变特征转移[6](Scale Invariant Feature Transform，SIFT)算法等，相比于区域匹配方法，特征匹配方法受光照以及形变等因素影响较小，可以得到比较可靠的结果。

第2类技术是在被测物体表面或者周围环境中人为布置若干具有定向反射性质的人工标志点[3]，这些标志点具有不同的形状图案，利用这些图案的特性，如找到图案的原点或交叉点，对标志点进行编码，进行编码的定向反射标志点称为“编码元”，每一个编码元进行唯一的身份标识后，就可以方便地进行多幅图像的匹配。这类方法操作简单，易于实际应用。本文主要采用此类方法进行研究和改进。

1 编码图案

迄今为止，在计算机测量领域编码图案的设计已经有很多种[7-12]，主要采用以下几种:圆形、方形、直线型，如图1所示。它们在编码的过程中都是根据自己的几何特性或沿着给定的路径进行解码。

图1 编码方案

通过对现有图案的分析与比较，圆形图案具有抗噪性强、提取精度高且易于提取的特点。考虑到圆形固有的优势，文献[12]提出了一种圆形靶标的设计方法，如图1f。而圆形编码方案涉及到椭圆中心的提取。在实际应用中，由于图像的旋转和光强等因素的影响，常常会出现椭圆中心的提取错误，现有的方法通常都忽略出错的编码点，这大大降低了图像点云的匹配精度，甚至一些关键编码点的提取错误将直接导致三维重建任务的失败。针对此种情况，本文提出对图案编码进行纠错的改进算法。将信道编码的可纠错编码技术用于编码点的设计，实现了编码元的自动识别、精确定位以及自动纠错等功能。

2 汉明码纠错性在编码中的应用

针对编码过程中出现的中心定位错误，提出可纠错的编码方案是需要切实关注的问题。可纠错的信道编码有多种，例如分组码、卷积码等，本文采用使用广泛的差错控制分组码汉明码进行纠错，如果采用n个码长的编码点a=(an－1，…，a1，a0)，其中信息元的位数是 k，则校验元的位数是n－k，则码字就以(n，k)表示，以(7，4)编码为例，可以建立如下的线性方程组

式(2)可以简写为H·AT=OT，

式(1)也可以改写成如下的矩阵形式

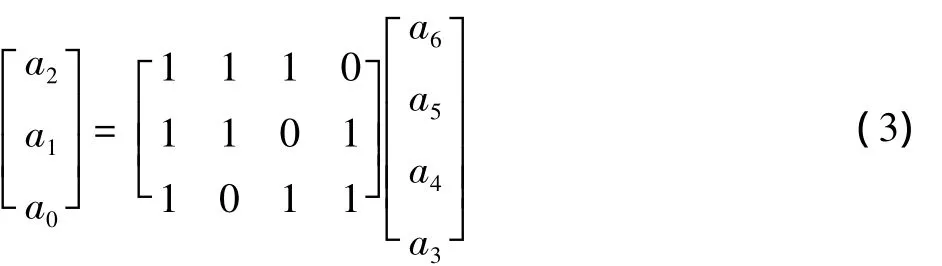
比较式(2)和式(3)，可以看出式(3)的右侧式子是矩阵H的一部分。

式(3)两侧作矩阵转置，得

矩阵G称为生成矩阵。

由生成矩阵G可以得到整个码组，如下公式所示

式(6)可以看出，任何一个码组都是生成矩阵G的各行的线性组合，得到表1。

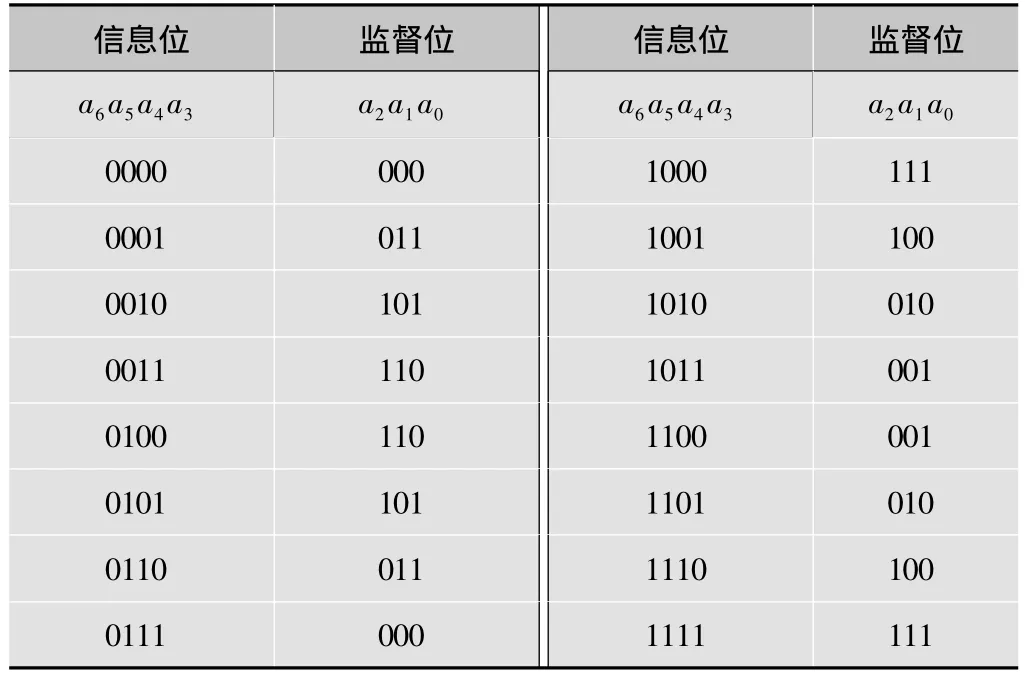
表1 纠错编码点

然而由于实际工作中各种因素的影响，CCD采集到的编码点经过识别后得到相应的编码，其表示为R，如果用c表示正确的编码，E表示错误图样，则

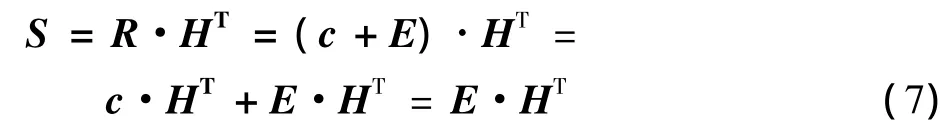
式中:S为伴随矩阵，其和错误图样对应，从而可进行编码点的纠错。

本例中伴随矩阵 S=[S1，S2，S3]，分别是3个监督式中的校正子，S的值与错码位置的对应关系如表2所示。

表2 校正子与错码位置

3 纠错编解码的设计方案

现有圆形的编码方案没有涉及到编码纠错问题，为了提高编码的抗噪能力，提出了一种新的纠错编码设计方案。

编码元全部由圆形组成，包括标志点、参考点与编码点，根据标志点所处的位置不同，可以设计2种不同的编码模式，如图2所示，本节以第2种编码模式进行说明。

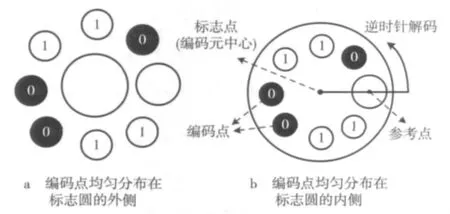
图2 编码图案，图示的编码值为0110011

如图2所示，标志点的半径最大，参考点和多个编码点等角度均匀地分布于标志点圆形内部周围。为了区别于编码点，参考点的半径大于编码点的半径。标志点的中心位置作为整个编码元的中心位置，参考点是编码元译码的起始点。

从参考点开始，逆时针旋转固定的角度进行读码，编码位上编码点的有无对应为二进制“0”和“1”，由编码点组成的不同序列代表不同的编码字。引入参考点的方法，使译码简单，确保了编码的唯一性，图2b给出了表1中1个7位编码长度的实例:0110011。

假设标志点对应的椭圆参数为 (X0，Y0，a0，b0，β0)，(Xc，Yc)是编码圆和参考圆成像后对应的椭圆中心，如图3a所示。在进行编码元识别之前，需要将椭圆图像进行逆投影变换，如图3b所示。

图3 圆形靶标坐标转换

解码的过程中，设编码长度为k，那么从参考点为起点，逆时针方向第i个编码(如果存在)位所对应的十进制权值为

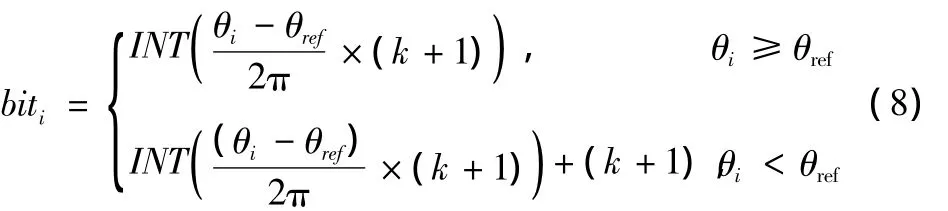
式中，INT表示取整运算。那么，最终得到编码元的编码值

在图像编解码的过程中，获取照片之后，首先应该进行边缘检测，其中Canny算子在边缘检测中具备非常好的检测效果，具有低误码率、高定位精度和抑制虚假边缘等优点;接着的工作是椭圆中心定位，现有的方法分别是最小二乘拟合法、变量含误差模型和基于HEIV模型的椭圆拟合方法;最后就是编码点的解码过程。如图4给出了图像编解码的流程。

图4 编解码的流程

4 纠错实验与现有编码点的比较

为了验证文中纠错编码点的可行性，做了实验进行验证。实验采用大恒DH-HV1351UM相机，像素分辨力为1280×1024。采用表1中的4种可纠错编码点(0100110)，(0011110)，(0101101)，(0110011)，编码长度7，编码元实际的物理尺寸为25 mm，最小的编码圆直径为4 mm，拍摄距离约1.5 m。设计的编码点如图5所示。

图5 编码点设计图

本文对编码点的解码过程应用编码识别和提取算法进行了MATLAB仿真实验，仿真的步骤如下:

1)对拍摄的图像去噪，设定阈值将图像二值化;

2)用Canny算法进行边缘检测;

3)进行轮廓跟踪将目标边缘点连成一条连续的边界，同时尽可能去除非目标边缘点;

4)目标粗识别;

5)根据边缘点进行椭圆的拟合，确定椭圆点的中心;

6)根据各个圆的半径，判断起始点并按照逆时针旋转角度43°，颜色为黑则灰度记为0，白则记为1，从而可以得到解码的编码点。

如图6所示，图6a为图像的求反图像，图6b为边缘检测和圆点中心的拟合结果。从图6b中可以看到，从上到下从左至右解码为(0100110)，(0011110)，(0101101)，(0111011)。

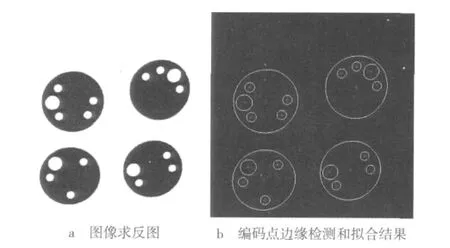
图6 编码点解码结果图

由此可以看出编码点的识别出现错误。根据本文介绍的改进算法，可以对错误码点进行纠错。这种改进算法与编码识别和提取的算法进行纠错能力对比，比较结果如表3所示。

表3 纠错能力对比

编码识别和提取的改进算法根据(4)式可知，将解码结果乘以H，得到4个伴随矩阵S:(000)，(000)，(000)，(011)。从伴随矩阵可以看出，第4幅图编码点出现了错误，这也从图6b中可以看出，未能检测出1个编码圆点的中心。解码错误在现有方法中是经常出现的问题，通过对比错误样图可以纠正错误的点，从而得到正确的编码点(0110011)。

5 小结

综上所述，本文提出的新的可纠错的编码点是可行的，并有较强的实用价值，其优点在于编码点由圆点组成，简单易行，同时将信息论中信道编码的理论用于编码点的设计，实现了编码点的自纠错性，较好地解决了实际应用中编码点识别错误的问题。经过实验验证，该方法在编码出现1位错误时可以实现自修正的功能。多个编码错误的识别与纠错是下一步研究的方向。

[1]CHE Chenggang，NI Jun.A ball-target-based extrinsic calibration technique for high-accuracy 3D metrology using off-the-shelf laser-stripe sensors[J].Precision Engineering，2000(24):210-219.

[2]WANG G J，WANG C C，FRANK S H.Reverse engineering of sculptured surfaces by four-axis non-contacting scanning[J].The international journal of Advanced Manufacturing Technology，1999(15):800-809.

[3]周晓刚.立体视觉测量技术中编码匹配方法研究[D].北京:北京机械工业学院，2003.

[4]POLLARD S B，MAYHEW J E，FRISBY J P.A stereo correspondence algorithm using a disparity gradient limit[J].Perception，1985，14(4):449-470.

[5]BAKER H H.Depth from edge and intensity based stereo[D].Illinois:University of Illinois at Urbina Chanmpaign，1981.

[6]LOWE D.G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60(2):91-110.

[7]FRASER C S.Automation in digital close-range photogrammetry[C]//Proc.First Trans Tasman Surveyors Conference.Newcastle，Australia:IEEE Press，1997:202-205.

[8]NIEDERYÖST M，MAAS H G.Automatic deformation measurement with a digital still video camera[C]//Proc.4 th Conference on optical 3D measurement techniques.Zurich，Switzerland:IEEE Press，1997:356-358.

[9]FORBES K，VOIGT A，BODIKA N.An inexpensive，automatic and accurate camera calibration method[EB/OL].[2012-04-03].http://www.prasa.org/proceedings/2002/prasa02-01.pdf.

[10]SHORTIS M R，SEAGER J W，ROBSON S，et al.Automatic recognition of coded targets based on a hough transform and segment matching[EB/OL].[2012-04-05].http://proceedings.spiedigitallibrary.org/proceedings.aspx?articleid=756122.

[11]DONG Mingli，ZHOU Xiaogang，ZHU Lianqing，et.al.Automated image matching with coded points in stereo vision measurement[J].Chi-nese Journal of mechanical Engineering，2005，18(3):453-456.

[12]AHN S J，RAUH W.Circular coded target for automation of optical 3D measurement and camera calibration[J].International Journal of Pattern Recognition and Artificial Intelligence，2001，15(6):905-919.