一种基于图的线性判别分析方法

王 飞，刘玉英，彭 超

(中国矿业大学信电学院，江苏 徐州 221116)

随着信息时代的发展，大量信息的涌入使得人们获得丰富的数据。如果仅从这些数据本身出发来寻找我们想要的信息，已经超出了人类以及计算机的能力范围。因而如何有效而合理地收集、组织以及分析这些数据是现代人们亟待解决的问题。基于图学习的方法就是解决这一问题的一类非常重要的方法。研究表明，很多降维方法最终可归结于图的构造和低维嵌入方式[1]。这类方法通常将整个数据集建模成为一张图，图上的结点G就是样本数据，S边表示数据之间的关系，通常用(G，S)表示。这样，数据的分析问题就转换成为图上的分析问题，因为图可以看作是流形的离散化形式，图上的结点是从数据流形上采样得到的，而图上的边则反映了某些数据流形的结构信息。这些方法的目标就是要学习一个更低维的数据嵌入并且保持原数据图的某些信息[2－3]，一些流行的降维方法如:等距离映射(Isomap)[4]主要保持数据点之间的测地距离，局部线性嵌(LLE)[5－6]主要保持数据的领域关系，Laplace特征嵌入(LE)[7]主要保持数据流行的光滑性。

同样，线性判别分析(LDA)[8]作为经典的降维方法，也可归结于图的构造方法范畴。LDA的核心思想是样本从高维映射到低维空间保证投影后，使得模式样本在新的空间中有最小的类内距离和最大的类间距离，从图构造的角度分析，LDA可理解为:首先构造类内样本图，使得类内所有样本点向该类中心靠拢;然后构造类间图，使得各类中心与总样本中心远离。然而LDA方法作为全局性降维方法，在处理类间样本分类时，只考虑总体样本中心点与各类样本点的分离的全局特性，忽略了样本间的边缘点的局部特性，从而可能导致类间边缘样本点的误分。本文从图构造的角度重新构造类间图，针对该问题提出了一种新的降维方法——K－边缘判别分析方法(KMDA)。从可视化分析和降维后分类效果两个方面分别对新提出的方法和LDA进行对比实验，数据库选择UCI上的公共数据集和人脸数据集，实验证明，该方法在分类正确率方面表现较好。

1 线性判别分析(LDA)

线性判别式分析(Linear Discriminant Analysis，LDA)，也叫做Fisher线性判别分析(FDA)，是模式识别的经典算法，基本思想是将高维的模式样本投影到低维的最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后尽量使同一类别的样本紧凑，而使不同类别的样本远离。因此，它是一种有效的特征抽取方法。使用这种方法能够使投影后模式样本的类间散布矩阵最大，并且同时类内散布矩阵最小。也就是说，它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离。具体算法如下:

设有C个模式类别，X=(x1，x2，…，xm)是N个m维的训练样本，类间离散度矩阵Sb和类内离散度矩阵Sw定义[7]

式中:ui是第i类样本的均值;u0是总体样本的均值;ni是属于i类的样本个数。当Sw非奇异时，Fisher准则最终的投影函数可定义为[8]

2 K－边缘判别分析方法(KMDA)

这里介绍一种新的方法——K－边缘判别分析方法(KMDA)，来控制边缘部分的点，重新建图，类似LDA构图思想，本方法首先使得样本类内紧凑，同时类间选择一类的中心，并求其他类中与这类中心的K个近邻点，最大化它们之间的距离，图1为该方法的基本思想。首先使得同类中所有点向该类中心靠拢;同时，使得该类中心与其他类的K个边缘点远离。

图1 K－边缘判别分析方法(KMDA)基本思想

2.1 类内紧凑

高维数据映射到低维应该保持类内间距离更加紧凑[9]，基于LDA思想，本文构造类内紧凑图Gc，设X={x1，x2，…，xn}∈Rm×n为训练样本，Y={y1，y2，…，yn}∈Rd×n为降维后训练样本的低维嵌入，n为样本数，m为样本维数，d为嵌入维数。Gc={X，S}为无向有权图，样本xi为图中一点，W为其相似度矩阵，Wij为样本i和样本j的相似度。可以通过式(3)进行优化

2.2 类间远离

降维的目的一般是为了以后做数据的分类或回归，前一节中尽量在降维的过程中保证类内紧凑，这一节在降维过程中要使类与类之间尽量远离，LDA算法通过求整体样本的中心和各个类的中心，从而使得每一类的中心与整体样本的中心远离，但是对于比较分散的数据样本，LDA算法容易导致边缘点的误分，根据MFA[10]思想，本文同样构造一惩罚图Gp，由于Gc已经保证了降维过程中各训练样本向中心紧凑，所以在类间，另一类的边缘可根据通过求与这类中心最近的K近邻来确定，K的选择一般根据训练样本的数量而定。优化公式为

2.3 构造投影矩阵

通过前两节图的构造以及优化后的公式，最终得到求解以下的优化问题

当Sc非奇异时，最佳投影矩阵wopt的列向量为广义特征方程Spα=λScα的d个最大的特征值所对应的特征向量。

具体算法如下:

1)首先检验样本数和维数的大小，即Sc是否奇异，如果奇异先运行PCA[11－12]降维，使得样本维数小于或等于样本个数。

2)构造如图1所示的类内和类间图求出最优化向量wopt。

3)计算出低维表示:Y=XWopt。

3 实验分析

3.1 可视化分析

Wine数据集是一个典型的机器学习标准数据集，本文首先选择Wine数据前两类进行分类实验，共130个样本，其中1～59为第一类，60～130为第二类，实验测试训练样本选择共66个，第一类和第二类分别33个，测试样本共64个，第一类和第二类分别为29和35个，为达到可视化效果，本实验分别运行LDA和KMDA分别把样本降到二维空间并对测试样本进行分类，结果如图2所示。

图2 分类结果对比(截图)

可见，当运行LDA分类时，由于在处理不同类间远离时，只注重全局性而忽略了边缘的个别点，从而导致边缘点的误分;KMDA算法在映射过程中强制选择不同类最近的K个点，使它们远离本类的中心;图2b为当边缘近邻值K=4时的KMDA分类结果，可以看出运行KMDA后，图2a中被误分的两个点，在图2b中得到正确的分类结果。

3.2 公共数据集测试

选取UCI中Wine数据集、Sonar数据集、Abalone数据集和Diabetes数据集进行对比实验，表1列出了每个数据集的实验参数。为达到对比的效果，本文降维后的分类器均选择1－NN分类，实验结果如图3所示，纵坐标表示降维之后采用1－NN分类的正确率，横坐标表示所降到的维数，实验目的是比较3种算法在不同数据集降维后的分类正确率。

表1 各个数据集实验参数

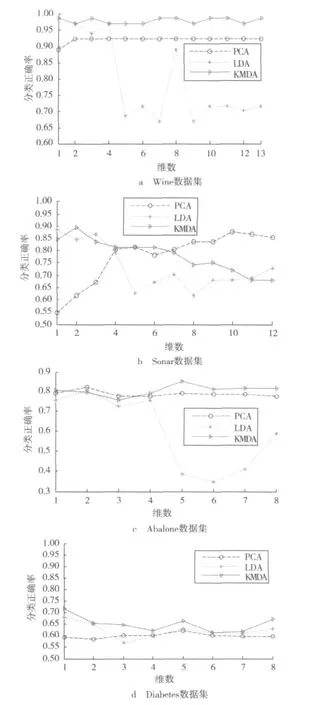
图3 3种算法在不同数据集降维后的分类正确率比较

从图中的曲线可以看出:就稳定性而言，PCA降到各个低维空间比LDA好;LDA在降到特定的低维空间时分类正确率比PCA效果好;从总体看来，无论比较稳定性还是最高分类正确率，KMDA效果最好。这是因为PCA在降维过程中，低维映射函数矩阵，选择的是主成分映射，当降到不同维数时，PCA能选择数据的主要特征，总体稳定性较好;而LDA使同类紧凑，不同类远离，注重分类效果;KMDA克服了LDA局部边缘点存在的问题，总体效果最佳。

3.3 人脸数据集测试

3.3.1 BioID 数据库

BioID标准人脸库是1521个384×286灰度自然场景下的人脸图像，由23个测试者提供。还包含每个人脸的双眼位置。图4是BioID人脸库中部分图片。

图4 BioID人脸库的部分图像

从BioID人脸库选取两个人共40幅图像做实验，以每人的前10幅图像作为训练样本，后10幅作为测试样本，这样训练样本和测试样本总数均为40。分别运行PCA，PCA+LDA，PCA+KMD算法降维，再分别选用1－NN分类器分类，最后得到识别率如表2所示。

表2 BioID数据库采用各算法降维后的分类正确率

3.3.2 JAFFE 数据库

JAFFE人脸数据库是在人脸表情识别研究中应用最多的数据库之一，从JAFFE人脸库中选择两个人脸图像做实验，每个人均选择前10幅图像做训练样本，后10幅作为测试样本，这样训练样本和测试样本总数均为20，先运行PCA算法，再分别运行LDA和KMDA算法，降到1～10维，最后采用1－NN分类器进行分类，分类正确率如表3所示。

表3 JAFFE数据库采用各算法降维后的分类正确率

由表2和表3可见，在同一种分类器1－NN下，在各个维度上，KMDA方法识别结果明显优于经典的LDA方法。其中的原因是，LDA方法在区分低维嵌入过程中，不同类间的分离是采用全局性嵌入，即在计算Sb时，用总体的均值减去每一类的均值，最后选取Sb的d个最大的特征值所对应的特征向量作为投影轴进行特征抽取，这样处理的结果可以使不同类之间远离的效果，但是容易忽略类间边缘局部点的类间划分，从而导致边缘点的误分;KMDA算法考虑到局部边缘点，计算Sb过程，首先选择最近的也是最容易误分的这些边缘点，使其远离异类的中心，而从表可看出，这种鉴别信息的方法是有效的。另外，当降到某个维数时三种算法最后的分类效果较差，如JAFFE数据库中，采用PCA+LDA，降到4维时分类正确率只有0.2，原因在于LDA和PCA都是全局性线性降维算法，而人脸数据库是一种非线性结构，这些方法在处理这些数据时，容易忽略局部数据信息。从整体看来，本文提出的算法效果较好。

4 结论

针对LDA在处理边缘点上存在的问题，本文提出了一种新的基于图的线性判别分析方法。该方法基于图学习的思想，重新构造图，使同类样本尽量紧凑的同时，避免了不同类之间边缘点的误分。实验中可以看出，新方法在降维过程中的分类正确率以及稳定性较好，与LDA方法相比有一定提高;不足之处在于K的选择上，本文实验K的选择是在从大量实验中得出的经验值。如何有效选择K值达到更好的效果是接下来要研究的内容。

[1]KOKIOPOULOU E，SAAD Y.Enhanced graph－based dimensionality reduction with repulsion Laplaceans[J].Pattern Recognition，2009，42(11):2392－2402.

[2]王飞.图上的半监督学习算法研究[D].北京:清华大学，2008.

[3]乔立山.基于图的降维技术研究及应用[D].南京:南京航天航空大学，2009.

[4]TENENBAUM J B，SILVA V D，LANGFORD J C.A global geometric framework for nonlinear dimensionality reduction[J].Science，2000，290:2319－2322.

[5]ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290:2323－2326.

[6]李白燕，李平，陈庆虎.基于改进的监督LLE人脸识别算法[J].电视技术，2011，35(19):105－108.

[7]BELKIN M，NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation，2003，15(6):1373－1396.

[8]边肇祺，张学工.模式识别[M].北京:清华大学出版社，2000.

[9]申中华，潘永惠，王士同.有监督的局部保留投影降维算法[J].模式识别与人工智能，2008，21(2):233－239.

[10]XU D，YAN S，TAO D，et al.Marginal fisher analysis and its variants for human gait recognition and content－based image retrieval[J].IEEE Trans.Image Processing，2007，16(11):2811－2821.

[11]ARTINEZ A M，KAK A C.PCA versus LDA[J].IEEE Trans.Pattern Analysis and Machine Intelligence，2001，23(2):228－233.

[12]罗丞，叶猛.PCA算法在P2P加密流量识别中的研究与应用[J].电视技术，2012，36(3):62－65.