基于Memetic算法的动态武器目标分配问题研究＊

刘传波

（武汉市74223信箱 武汉 430074）

1 引言

武器目标分配（Weapon Target Assignment，WTA）问题的研究是目前防空领域作战指挥决策所需解决的重点和难点问题。传统意义上的静态武器目标分配（Static Weapon Target Assignment，SWTA）问题的研究已不满足在实际作战指挥决策的需求，由于目标在时间和空间上出现的不确定性，使得部分武器不能及时投入战斗，同时，新目标的出现使得分配过程变得更加复杂。考虑时间因素影响的动态武器目标分配（Dynamic Weapon Target Assignment，DWTA）问题研究逐渐成为近年来研究的重要方向。

目前对DWTA问题的研究主要集中在寻求一种有效的智能算法来解决时间因素对分配过程的影响，提高动态分配的及时性和合理性。文献［1］提出了“时间窗（Time-Window）”的概念用以描述时间约束，用一种混合遗传算法来解决DWTA问题；文献［2］运用约束规划方法建立了DWTA问题的约束满足问题，并提出了一种随机变邻域禁忌搜索算法对模型进行求解；文献［3］和［4］针对有截止期的DWTA问题，利用元级控制过程控制改进型遗传算法的响应时间，提出一种元级控制策略来提高解的效用。文献［5］和［6］分别提出了基于贪婪局部搜索的 Memetic算法和基于禁忌搜索拍卖算法来解决具有带约束的DWTA问题。上述研究结果要么仍局限于静态分配的思想，要么未从分配的动态过程来解决该问题。尽管DWTA问题并未得到完整解决，但在许多实际应用中，通过放宽某些约束条件或增加某些假设条件可以得到一些特殊情况（如所有武器完全一样的情况）下的最优解，或一般情况下的近似解。同时必须注意到只有把分配过程中的动态随机事件考虑在内，才能得到对实际应用更为有效的武器目标分配算法。

本文分析了动态武器目标分配问题的特点，建立了具有时间和空间约束的DWTA数学模型，提出了一种自适应Memetic算法来解决该问题，该算法结合遗传算法和模拟退火算法的特性，有效提高全局和局部搜索的能力，并采用一种有限时间控制策略来提高满意解的输出质量，能及时应对随机事件（新目标的出现）对前期优化过程的控制和重构。

2 DWTA问题的描述和数学模型构建

2.1 问题描述

由于目标群的出现是一个随机过程，且武器系统的空间分布存在不同的状态，不同类型目标出现的时空分布不同，因此，对于DWTA问题的研究十分复杂，目前的研究主要针对特定的作战态势，作一定的假设条件来简化问题的复杂性，由浅入深的思路来分析该问题。本文假设防空武器系统由分布在n个平台的m个同类武器单元组成，武器总数为W＝n·m，且各单元类型相同；目标类型和速度相同，均处于匀速直线飞行的巡航段。初始状态下，系统根据武器单元状态和已探测到的目标状态信息，计算并输出优化分配方案对目标拦截作为一个时间阶段。因此防空作战过程可划分为不确定的K个阶段，DWTA优化过程是通过有限时间内合理分配各个阶段的“武器目标对”方案，最终实现最小化目标群的突防概率，或最大化系统防空拦截效率。

1）目标的空间约束。设目标j对应N个平台的航路捷径向量Pj＝［pj1pj2… pjn］，目标对应各武器平台所在位置的航路捷径Pji是否小于其最大航路捷径Pimax，且i＝1，2，…，n。即满足条件：

若满足，则可确定目标j处在平台集合N′的作战空域内，N′∈N。

2）目标的时间约束。目标的时间约束是建立在满足目标空间约束的基础上，进入同一平台武器发射区内的目标集合，从分配决策开始，按目标到达发射区近界的时间，分别进行排序，选择最先到达的目标所需时间为分配的截止期。其中，目标截止期计算的近似方法如下：取武器目标分配决策开始时刻，目标j所在位置点为（x，y），对应平台航路角为α，则根据几何关系，（x，y）与到达发射区近界位置点（x′，y′）有如下关系：

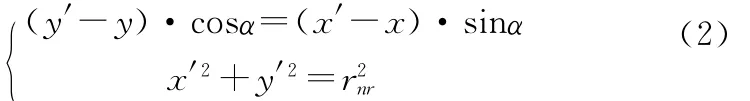
则目标到发射区近界的时间间隔ts为

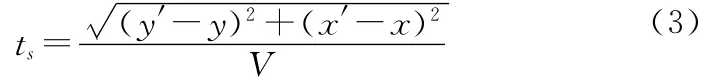
假设有四个目标T1～T4被探测到时正处于武器的发射区之外，它们到达发射区近界的所需时间分别是t1～t4，因而ti（i＝1，…，4）是完成对目标Ti（i＝1，…，4）分配武器的截止期。假设t4＜t3＜t1＜t2，按照到来时间的先后顺序建立所有正在处理中的目标的截止期，则最先到来的截止期是t4，它所对应的目标是T4，因此算法应以完成对目标T4的武器分配为停止准则。而针对该态势下的静态的武器目标分配则是不考虑有效打击时间，将四个武器同时分配给四个目标。

2.2 数学模型的建立

将拦截之后的目标的总期望剩余威胁值作为目标函数，假设武器对目标的拦截和毁伤都是相互独立的，则在第k（k＝1，2，…，K）时间段的武器目标分配数学描述如下：

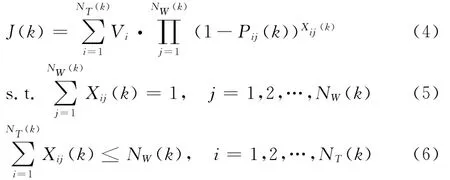
其中，NW（k）为武器数量，NT（k）为目标数量，Vi为第i个目标的威胁值，Pij为第j个武器用于拦截第i个目标的毁伤概率；Xij（k）为布尔值，表示第j个武器对第i个目标的分配决策变量，若分配则为1，否则为0。式（5）表示一个武器只能拦截一个目标，式（6）表示最多可拦截的目标数量不大于武器数量NW（k）。

则整个时间段K内总的目标函数为

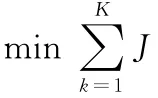
3 Memetic算法的设计概述

3.1 Memetic算法概述

Memetic算法是Moscato等人于1989年首先提出的一种较宽松的优化算法框架，或算法设计思想［7］。采用不同的搜索策略可构成不同的 Memetic算法，如全局搜索策略采用遗传算法、进化策略、粒子群算法、鱼群算法等，局部搜索策略采用爬山搜索、模拟退火、贪婪算法、禁忌搜索、导引式局部搜索等［8～10］。其实现遵循如下框架：

步骤1：根据具体优化问题，选择并确定全局和局部搜索策略。

步骤2：初始化种群。

步骤3：种群的全局搜索。

步骤4：个体的局部搜索。

步骤5：种群的局部更新。

步骤6：判断终止条件。若满足，算法停止；否则，返回步骤3。

3.2 关键参数和操作设计

Memetic算法作为一种混合算法框架，其各个环节存在多种可实施的策略，根据上述DWTA问题的描述，本文提出一种自适应的Memetic算法来解决该问题。其中，适应度函数为目标函数，全局搜索策略采用遗传算法，局部搜索策略采用模拟退火算法。下面分别从五个方面进行设计：

1）种群的产生。通常的算法而言初始种群是随机产生的，若按随机的方式生成初始群体，则在搜索的过程中耗时长且可能得不到最优解。对于DWTA问题，则可根据给定目标群初始状态，计算对应的空间约束，来确定可选的种群，排除无效个体，从而提高种群的优化效率；

2）进化操作。进化操作分别采用遗传算法中的交叉和变异算子，以确保子代能够遗传父代的主要特征。

初始状态下，交叉操作选择单点顺序交叉法，该方法具体过程为：设两父串为A、B，随机选择交叉点，定义交叉点后为匹配区域，将A和B的匹配区域分别加到B和A的前面，然后分别在匹配区域后依次删除与匹配区域相同的码得新的子串，如：

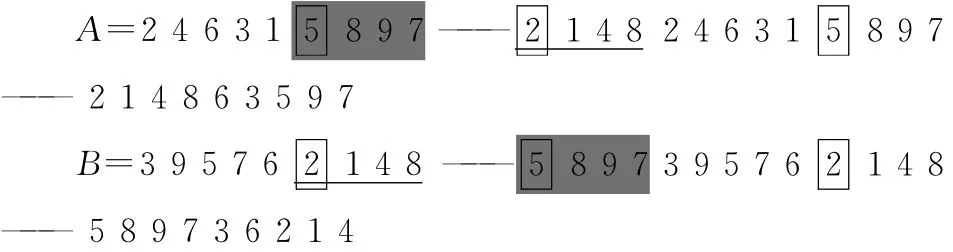
变异操作选择对换变异法，即随机选择串中非禁止位的两点，交换其值获得新串。如：当分配过程达到初始目标时间截止期时，设定对应武器目标对为禁止位，单点顺序交叉后，变：如目标3分配给武器4，则A［4］＝B［4］＝3为禁止位，有：

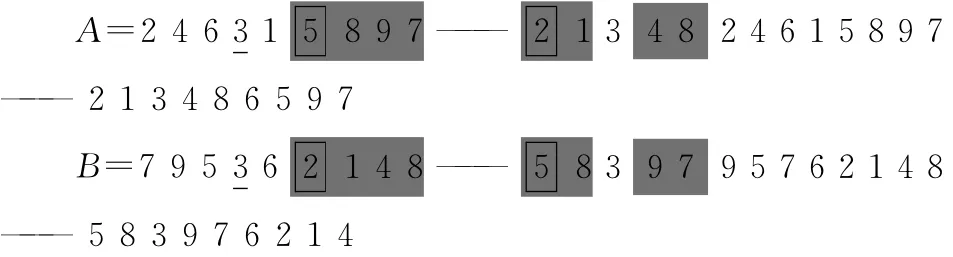
变异操作选择对换变异法，即随机选择串中除禁止位以外的两点，交换其值获得新串。

3）局部搜索。局部搜索的过程是优选局部优秀个体的过程，其关键问题主要在于：邻域空间的选择要使得优化效率和优化时间两者的折中，局部搜索策略的选择要针对具体问题的特点进行考虑，局部搜索在算法流程中的位置需保证优化效率为前提。因此，本文采用一种改进的模拟退火算法来进行邻域搜索，其伪代码如下：

4）种群的选择与更新。经过进化操作和局部搜索后，采用锦标赛选择等方法优选出新的个体来更新种群。锦标赛法在选择时，从种群中随机地选取k个个体，找出这k个个体中适应值最好的个体作为最优个体，这个最优个体就是下一代种群中的一个个体，这个过程重复n次就产生了新的种群。尽管该方法随机性更强，存在更大的随机误差，但是有较大概率保证最优个体被选择，最差的个体被淘汰。

5）终止准则。以算法运行到规定的时间截止期来输出结果，或目标函数在时间截止期内达到规定的精度，则输出结果。

3.3 一种自适应的Memetic算法流程设计

该算法的设计包括如下步骤：

1）确定空间约束下武器目标集合；

2）计算目标对应武器作战空域的时间截止期，得出目标集对应的时间截止期递增序列向量Tstop；

3）执行Memetic算法，判断算法执行时间t是否到达Tstop（1），若到达，输出对应的分配方案，取Tstop（1）中目标对应武器位为禁止位，继续执行算法，依次输出Tstop（2）…Tstop（N），目标分配完毕后，算法停止。

算法对新目标出现处理策略：

（1）新目标出现时，未有武器空闲，则等待武器射击完毕后再分配；

（2）新目标出现时，有武器空闲，计算目标对应的时间截止期，依次按Memetic算法对其进行分配。

4 实例

假设防御方探测到一批目标来袭，根据目标航迹信息计算目标群的空间约束，其中，有20个目标即进入某作战空域，由分配在不同平台的20个武器单元对目标进行拦截，目标威胁程度分别在［0.2 0.9］内随机生成，武器对目标的毁伤概率在［0.2 0.9］随机生成。初始状态计算目标的截止期，并升序排列，如表1所示：

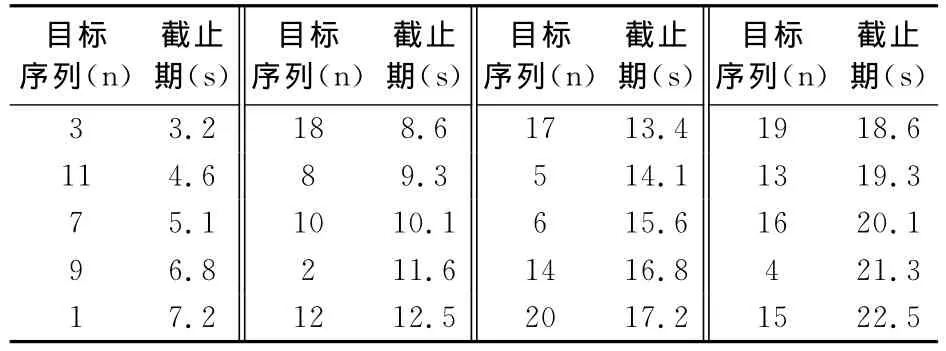
表1 目标序列及截止期

根据目标截止期，依次执行Memetic算法，分别获得武器目标分配方案，至第20个目标分配完毕，最终分配方案如表2所示。

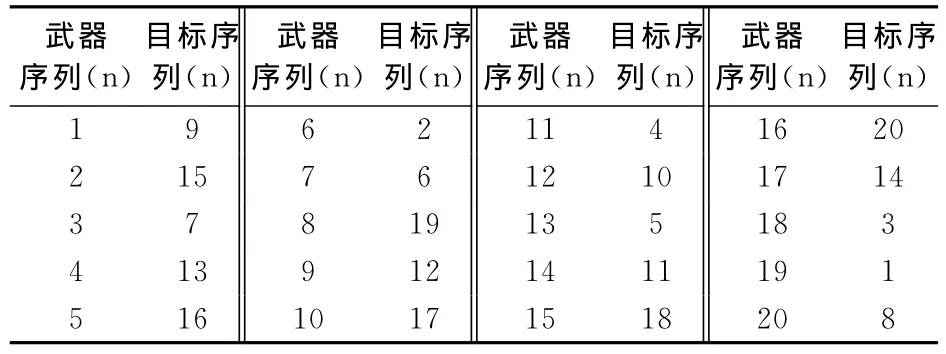
表2 武器目标分配方案

如图1所示为最优适应度值随进化代数和算法运行时间变化的曲线图，其中，曲线中分布的圆点为每一个目标截止期对应的最优适应度值和进化代数值，该算法最终执行完毕获得的最优适应度值为9.6009。如图2所示为Memetic算法与单纯遗传算法和模拟退火算法的最优适应度值随时间变化的迭代曲线。在给定的时间截止期，Memetic算法的最优适应度值优于其他两种算法，而单纯遗传算法和模拟退火算法易陷入局部最优解。

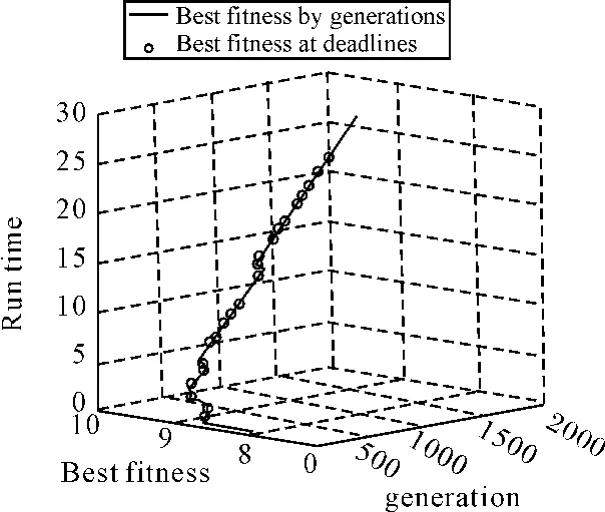
图1 Memetic算法迭代曲线图

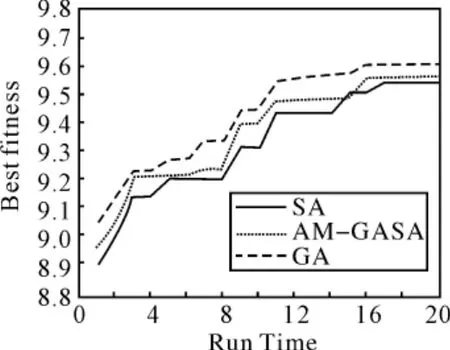
图2 三种算法收敛曲线图

根据仿真输出结果分析，本文提出的算法相比传统智能算法具有任意时间输出的特性。首先，它集中了GA的全局搜索能力和SA的局部搜索能力，能高效地跳出局部最优解，算法性能高；其次，能在不破坏算法运行状态的情况下，及时输出规定时间内满意解；同时，针对新目标的出现，算法能够动态地调整优化过程，符合实际武器目标分配需求。

5 结语

本文针对带空间和时间约束的DWTA问题，首先建立平台武器对目标的空间约束，计算带空间约束下目标对武器发射区的时间截止期，并在此基础上，提出了一种Memetic算法解决带时间截止期的动态分配过程。该算法在运行过程具备Anytime特性，能有效输出有效时间约束下的满意解，同时能够灵活地处理新目标出现对前一阶段武器目标分配过程的影响。该问题的解决对于深入研究满足实际应用条件的武器目标分配问题具有深刻的现实意义，提高算法处理的时效性和灵活性是下一步研究的重点问题。

［1］Khosla D.Hybrid genetic approach for the dynamic weapon-target allocation problem［C］.Proceeding of SPIE，2001，4396：248-263.

［2］陈英武，蔡怀平，邢立宁.SVNTS算法的动态武器目标分配问题研究［J］.计算机工程与应用，2006（31）：7-10.

［3］Cai Huaiping，Liu Jingxu，Chen Yingwu，et al.Survey of the research on dynamic weapon-target assignment problem［J］.Journal of Systems Engineering and Electronics，2006，17（3）：559-565.

［4］Wu Ling，Wang H，Lu Faxing.An anytime algorithm based on modified GA for dynamic weapon-target allocation problem［C］.WCCI，Hong Kong，China，2008：234-238.

［5］Peng Li，Ling Wu，Faxing Lu.Analysis on influential factors for meta-level control of the anytime algorithm for dynamic WTA problem［C］.ISA，Wuhan，China，2009：1-4.

［6］Chen Jie，Xin Bin，Peng Zhihong，et al.Evolutionary decisionmaking for the dynamic weapon-target assignment problem，Sci China Ser F-inf Sci，2009，52（11）：2006-2018.

［7］Moscato P.On evolution，search，optimization，genetic algorithms and martial arts：towards Memetic algorithms［R］.California：California Institute of Technology，1989.

［8］Paulo V W，Wong T，Sabourin R.A multi-objective memetic algorithm for intelligent feature extraction［C］.Proceeding of the Third International Conference on Evolutionary Multi-Criterion Optimization.Mexico：Guanajuato，2005：663-672.

［9］Berreta R，Rodrigues L F.A memetic algorithm for a multistage capacitated lot-sizing problem ［J］.Int.J.Production Economics，2004，87（1）：67-81.

［10］Xiuping Guo，Genke Yang，Zhiming Wu.A hybrid self-adjusted memetic alogorithm for multi-objective optimization ［C］.Fourth Mexican International Conference on Artficial Intelligence.Berlin：Springer Verlag，2004：542-548.