一种基于时域的欠定盲源分离方法

王荣杰 詹宜巨 周海峰 杨林举

（1.集美大学轮机工程学院 厦门 361021 2.中山大学工学院 广州 510006 3.中山大学信息科学与技术学院 广州 510006）

1 引言

近年来，鉴于盲源分离（Blind Source Separation，BSS）独特的数学模型，被作为一种重要的技术广泛应用于数字通信、机器人导航、生物医学工程、语音处理和图像处理等领域[1-5]。所谓的BSS，就是在源信号和混合系统（或传输通道）等未知的情况下，仅根据源信号有限的统计特性，从观测信号中恢复或估计出所有的源信号。根据观测信号和源信号的个数，盲源分离可分为非欠定盲源分离和欠定盲源分离（Underdetermined Blind Source Separation,UBSS）；相比之下，欠定盲源分离不如非欠定盲源分离技术成熟，而源信号个数多于观测信号个数的欠定盲源分离方法是本文的研究重点。传统的欠定盲源分离算法主要可分为两类：一类是基于源信号的稀疏性来处理，文献[6]提出利用聚类技术和最小化L1范数相结合的方法来恢复在时域上稀疏的源信号；文献[7,8]通过时频变换技术将时域非稀疏的源信号变换到稀疏表示的时频域，认为在时频域某些点上只有几个源信号存在，这类方法需先估计混合矩阵，然后再通过优化算法恢复源信号等两个步骤完成；另一类是利用广义分布模型作为源信号的概率密度函数的贝叶斯估计法[9,10]，这类方法的主要缺点是计算量大，一定程度上会降低源信号的恢复质量。盲源抽取（Blind Source Extraction,BSE）是BSS技术的一种扩展；但与BSS不同，它的目的是从观测信号中恢复一个或部分源信号，具有计算灵活简单等优点。现有解决BSE问题的算法主要两类：一类是通过优化基于高阶统计量（High-order Statistics,HOS）的代价函数来实现[11]，该类算法要求源信号为非高斯；另一类是基于二阶统计特性的算法，可克服基于HOS算法中源信号非高斯性的限制，但它们都需要两步来实现[12]，首先通过预白化观测信号得到混合矩阵的正交矩阵，然后再通过联合对角化合适的协方差矩阵得到白化阶段的正交矩阵。这些盲抽取算法只适合于非欠定的情况，本文提出一种基于时域的欠定盲源分离方法，该方法首先采用一种基于差分峰度的算法抽取欠定情况下的非平稳源信号，然后在非欠定情况下利用源信号的二阶统计特征分离剩余的源信号。

2 问题的描述

假设n个彼此相互独立的未知源信号，通过一未知瞬时线性混合系统后，得到m维观测信号矢量。观测信号x(t) 与源信号s(t) 的数学模型可描述为

在m≥n非欠定的情况下，给定A，源信号s(t)可由式（2）估计得到

式中，A*为A的广义逆矩阵，

当m＜n时，即为欠定情况，既便A已知，对于源信号s(t) 的恢复也不是唯一，只能通过估计方法估计出s(t) 的最优估计值。

盲抽取的主导思想是仅根据源信号的统计独立假设条件，从观测信号矢量x(t) 中逐个地分离出源信号，通过多次分离过程最终获得所有源信号的估计。文献[13]中m≥n情况下的盲源抽取过程可由式（3）～式（5）来描述。

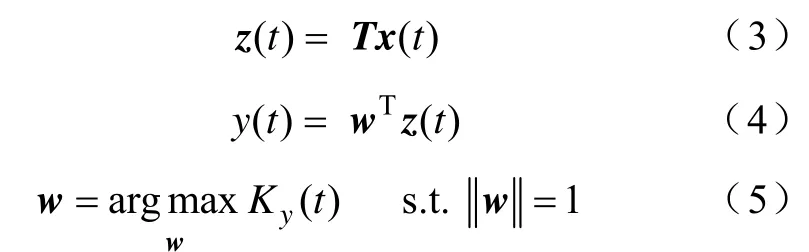
式（3）～式（5）中，y(t) 为一个源信号s(t)的估计，T为白化矩阵，抽取权矢量w为一个m维的列矢量，y(t) 的峰度y(t)]，具体的计算为E[·]为求均值运算。记，当行矢量g中只有一个元素为1，其余为0时，则y(t) 为在s(t) 中与g中元素为1位置相对应源信号的恢复或估计，但这种算法不适于m＜n的欠定情况。

3 基于时域的欠定盲源分离方法

本文提出的基于时域的欠定盲源分离方法，首先在引入文献[14]中差分峰度概念的基础上采用一种新的算法逐次分离欠定情况下的非平稳信号[15]，然后再利用源信号的二阶统计量恢复其余的源信号。

3.1 欠定的非平稳信号盲抽取算法

假设t1时刻的峰度为Ky(t1)，t2时刻的峰度为Ky(t2)，定义抽取后的估计信号的差分峰度则为

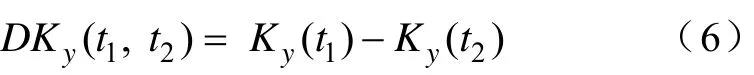
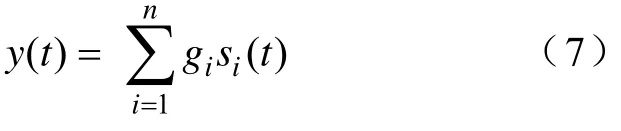
由式（6）可得到Ky(t) 和DKy(t1,t2) 的展开式分别为

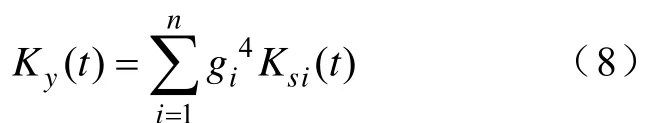
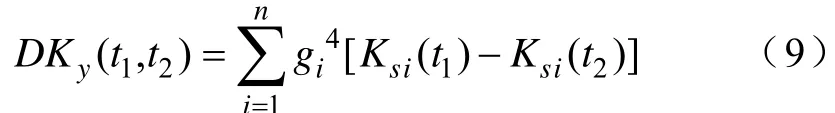
式中，Ksi(t) 为源信号si在t时刻的峰度。

当si(t) 为平稳信号时，式（9）中的Ksi(t1)-Ksi(t2)=0；而当源信号si(t) 为非平稳信号时，式中的Ksi(t1)-Ksi(t2)≠0。因此，式中的DKy(t1,t2) 是由非平稳si(t) 的元素组成的。如果令Q为非平稳源信号si(t) 的序号i集合，式（9）可改写成式（10）。

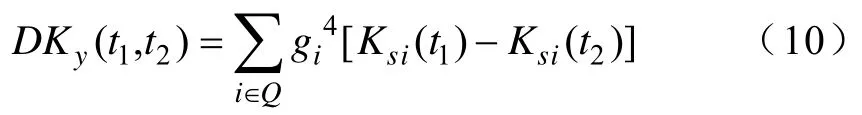
由于式（5）中的峰度K y(t) 是在白化观测信号x(t) 的基础上进行计算，同样计算式（6）或式（10）的DKy(t1,t2) 也需要预白化观测信号x(t)，它的白化矩阵T要满足式（11）的要求。

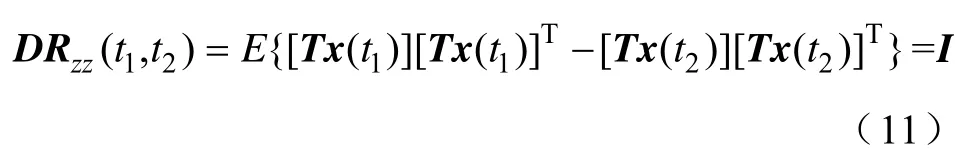
式中，I为单位矩阵。

为了满足式（11）的要求，T由式（12）进行特征值分解（Eigenvalue Decomposition,EVD）获得[15,16]。

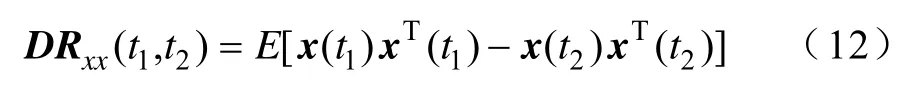
由上述分析可知，在m＜n的欠定情况下可通过优化式（13）获得最优的抽取权矢量w。

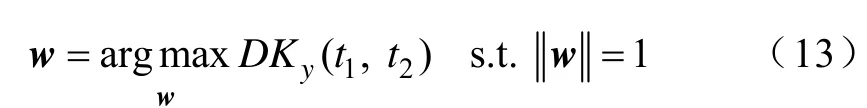
3.2 利用二阶统计量的盲源抽取算法

式（3）、式（5）描述为需要白化观测信号的非欠定盲源抽取过程。为了克服传统的基于HOS方法非高斯性的限制，且减少计算量，本节考虑了不需要预白化处理的抽取算法，该算法还可以实现在线盲抽取。注意本文仅分析离线的盲抽取算法。由此，可将式（4）改成式（14）。

如果式（14）中y(t) 的前p个时序信号的线性预测估计为yˆ(t)，那么它可描述成

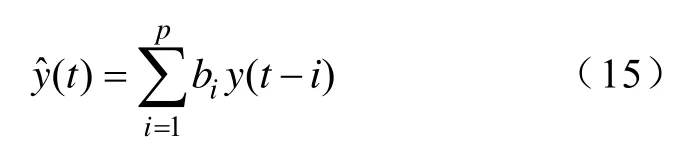
式中，bi为线性预测系数；i为时延。

对于平稳的信号，y(t) 与它的最优估计yˆ(t)的关系可由式（16）或式（17）描述[17]。

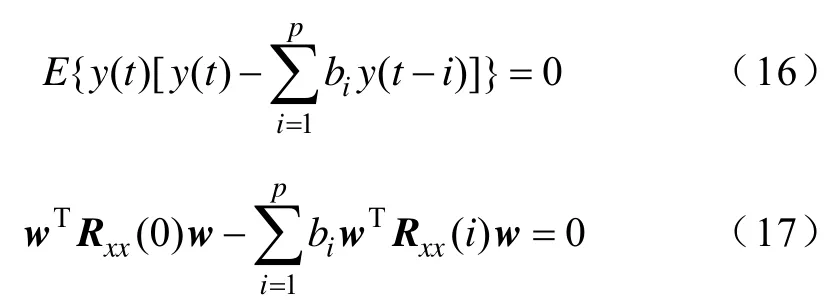
式中

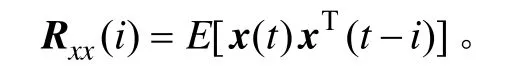
基于上述分析，本文将式（17）作为用于估计式（14）中抽取权矢量w的代价函数；将式中的时延i用时间间隔τ代替，而p用最大时间间隔Γ代替，为了不增加计算复杂度，bi取为1/Γ，由此可得到归一化后新的代价函数为式（18）。

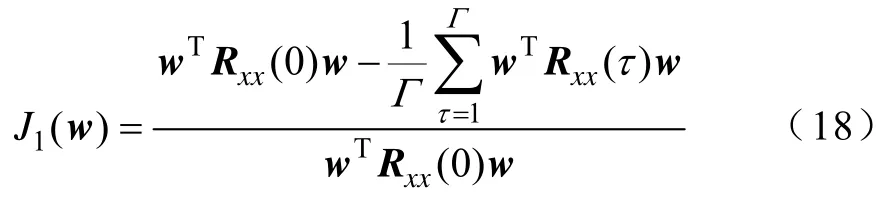
由此可得，式（14）中的抽取权矢量w可通过最小化式（18）中的代价函数获得，其过程为

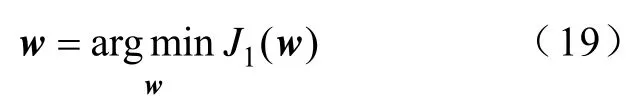
下面将对式（18）的代价函数的可行性进行分析。为了便于分析，式（18）中的时间间隔只取τ，则式（19）中的抽取权矢量w可通过求解式（20）的广义特征矢量获得[18]。

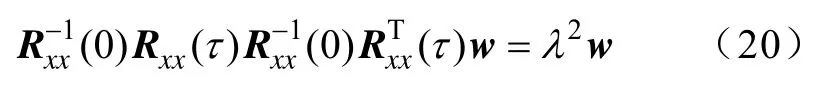
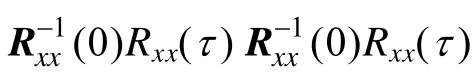
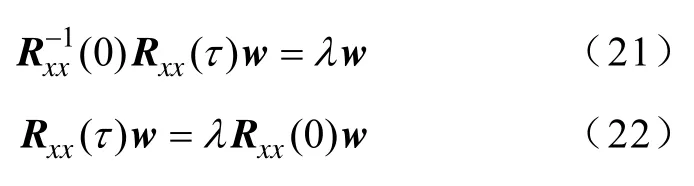
由式（21）～式（22）可知，w也是Rxx(τ) 和Rxx(0) 的广义特征矢量。不失一般性，由于Rxx(0)对角上的元素可变换为1，其代价函数可改写为

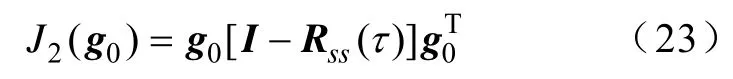
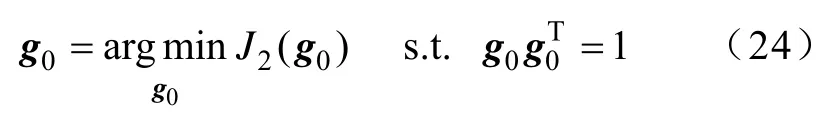
由式（24）可知，由于约束项的存在，使得g0可能的优化解肯定不是零矢量。当g0=g0,opt时，式（23）中的代价函数J2(w) 才达到最小，源信号才能被抽取（分离）出来。而g=wTA，所以只有w=wopt时，g0才能达到最优的g0,opt。

为了满足Rxx(τ)=RTxx(τ) 这一条件，式（18）中的Rxx(τ) 由式（25）估算得到。对于非平稳信号，根据它具有的全局非平稳局部平稳特性，将式（25）改写为式（26）。

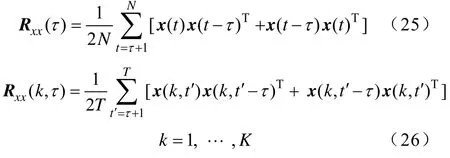
式（26）中，将N个x(t) 分解成K块不重叠的时序，每块时序的长度T=N/K。那么非平稳信号相应的代价函数和抽取权矢量分别由式（27）、式（28）来描述。

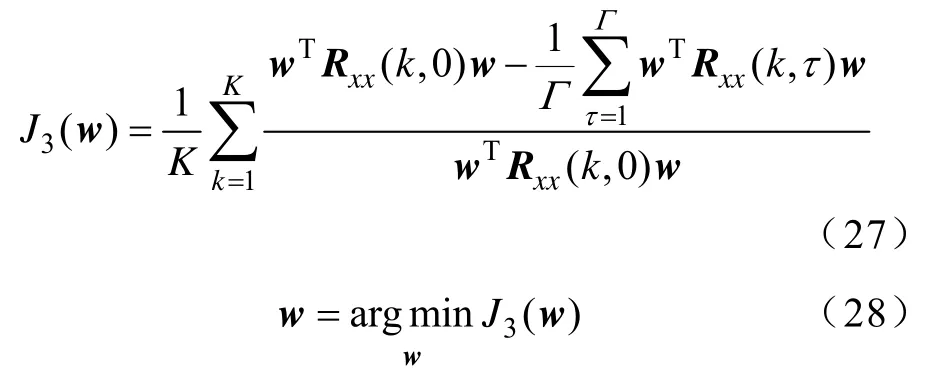
式（18）和式（25）可分别视为式（26）、式（27）的特殊形式；当K=1时，式（26）、式（27）将退化为式（25）和式（18）。

3.3 退化过程

退化过程包括退化处理和降维。退化处理的目的是从混叠的观测信号中减去已抽取的信号，这个过程可由式（29）描述。

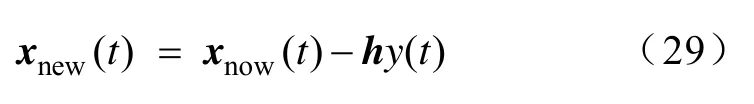
4 仿真实验分析

为了便于分析，图1中的伪代码描述了本文提出的基于时域的欠定盲源分离方法实现步骤。

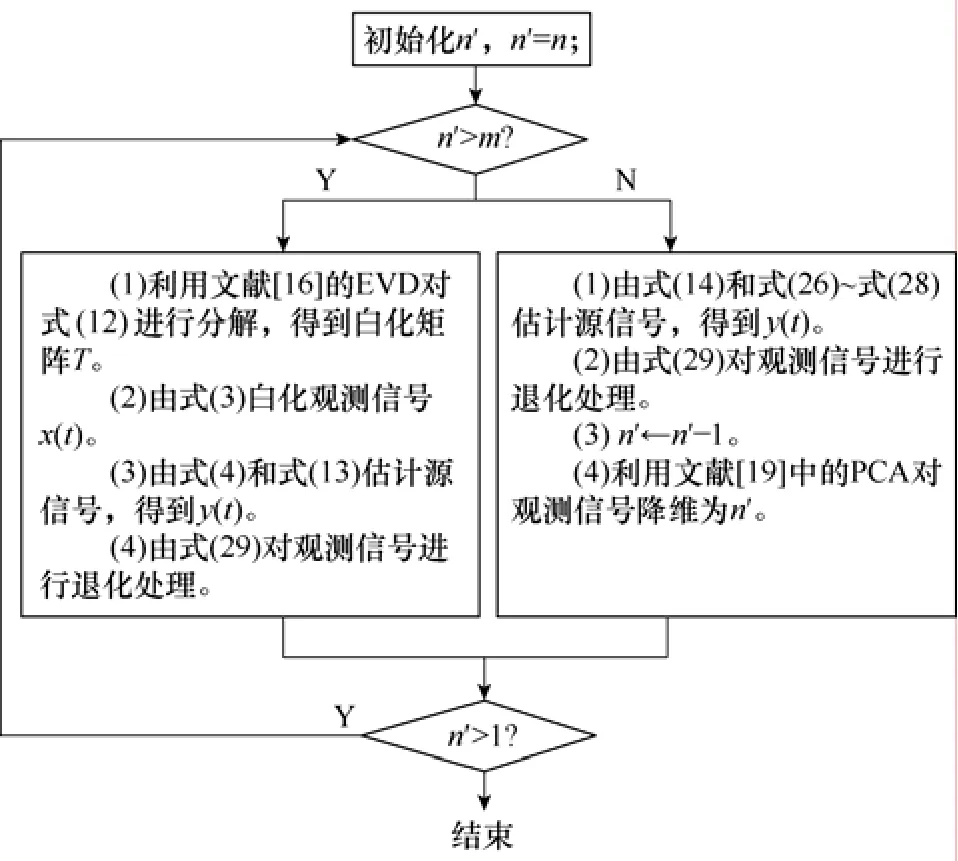
图1 基于时域的欠定盲源分离方法的实现步骤Fig.1 Realization step of method of underdetermined blind source separation in time-domain

为了验证3.2节中利用二阶统计量的盲源抽取算法的有效性，将该算法与文献[11]和文献[20]的BSE算法进行仿真比较分析，三种不同BSE的复杂度运算量见表1。在这个仿真实验中，源信号如图2a所示，s1和s2为非平稳的超高斯分布语音信号，它们取自文献[21]；s3为平稳的亚高斯分布正弦信号，s4为在randn[-1 1]之间随机产生的高斯白噪声信号。式（1）中的混叠矩阵A在[-1 1]之间随机产生，它的值见式（30），图2b所示为源信号经A混合后的观测信号。为了定量分析分离效果，本文采用式（31）、式（32）来评价盲源抽取算法的估计性能。图2c～2e分别为三种不同BSE算法的分离信号，它们的估计性能比较结果见表2。

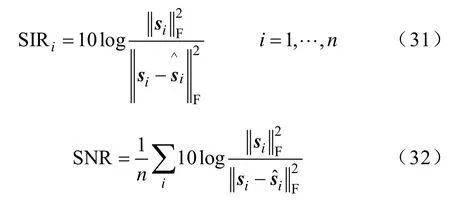
说明1：L为收敛迭代次数；由于Γ≪T，所以KΓ≪N。

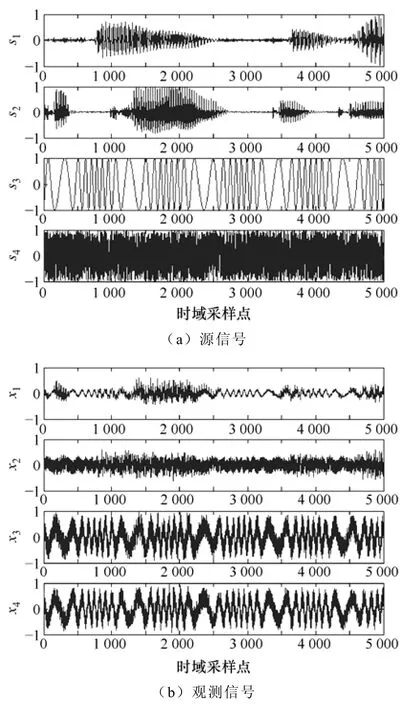
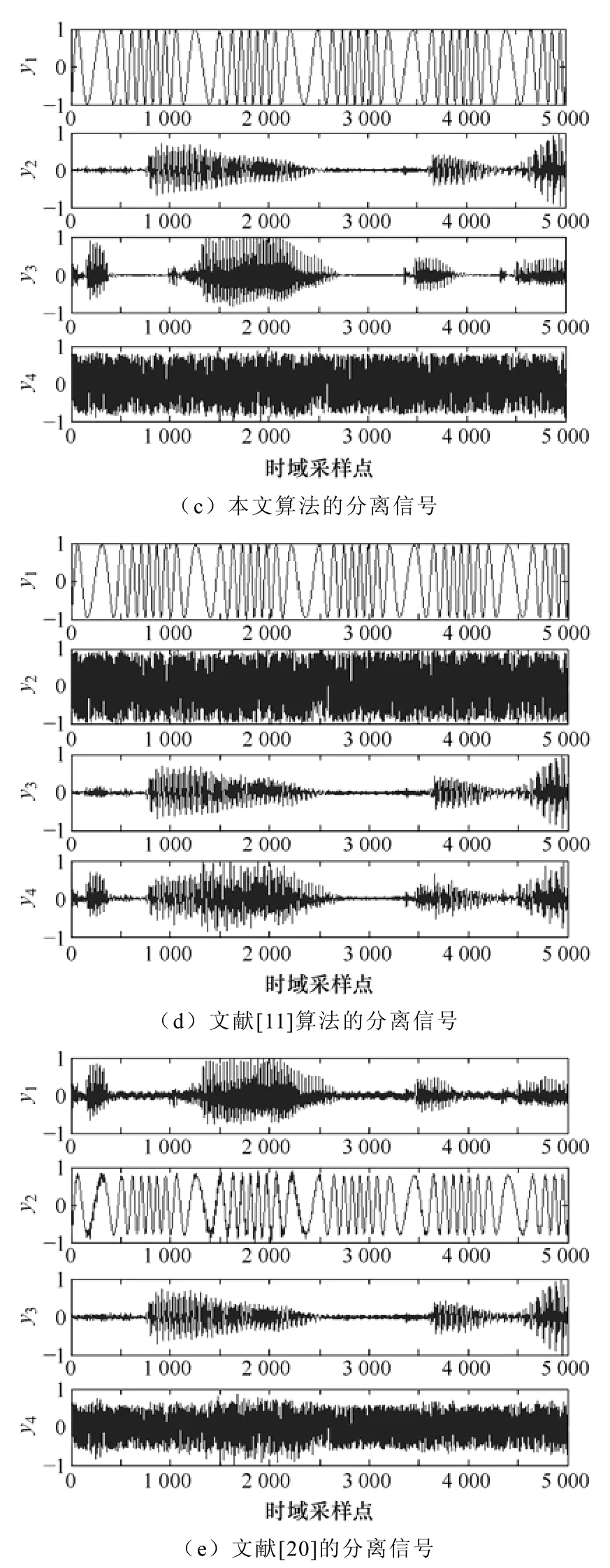
图2 不同BSE算法的分离信号Fig.2 Separated Signals of Different BSE Algorithms

表1 不同BSE算法计算复杂度的比较Tab.1 Comparison of computational loads of different BSE algorithms

（续）

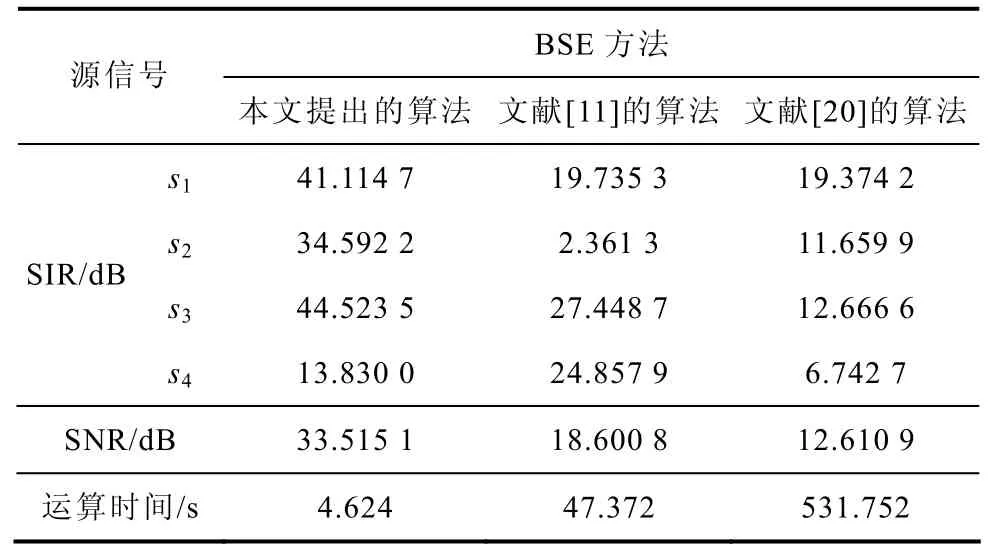
表2 不同BSE算法分离结果的比较Tab.2 Comparison of results of different BSE algorithms

说明2：仿真实验中，式（26）、式（27）中的L=5，K=5，文献[20]的算法中G(u) 函数选log(cosh(u))；表中的结果为10次独立仿真结果的平均值。计算用的是处理器主频为3.4GHz双核的DELL台式电脑。

通过图2和表1、表2中对三种不同的BSE算法进行比较的结果可知，虽然文献[11]的算法比本文算法对高斯白噪声信号的恢复质量高，但比较其余源信号的恢复质量，本文的算法不仅可以克服非高斯性的限制，具有更强的抑制高斯白噪声的能力，而且具有更好的分离效果。

为了全面评价本文提出的基于时域的欠定盲源分离方法的有效性，还将该方法与文献[7]和文献[9]的UBSS方法进行比较加以验证。仿真实验中的源信号如图3a所示，s1和s2为服从亚高斯分布的256×256图像信号，图中的横坐标和纵坐标代表图像的像素，逐行扫描后为一维信号；s3和s4为服从超高斯分布的语音信号。式（33）中的A同样在[-1 1]之间随机产生，图3b为混合后的观测信号，图3c～3e分别为三种不同的UBSS方法的分离信号，图像信号和语音信号的恢复性能分别由式（34）和式（31）来评价，利用它们对不同UBSS方法估计性能比较见表3。

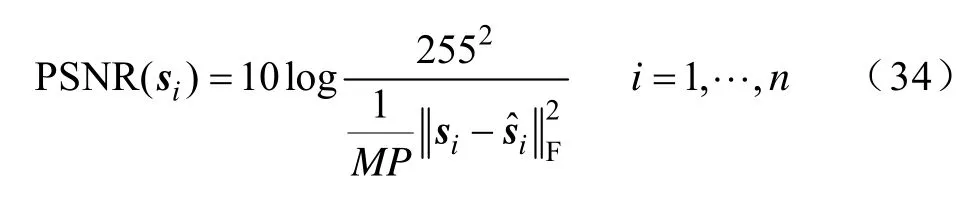
式中，M和P分别代表二维图像信号的行和列像素数。

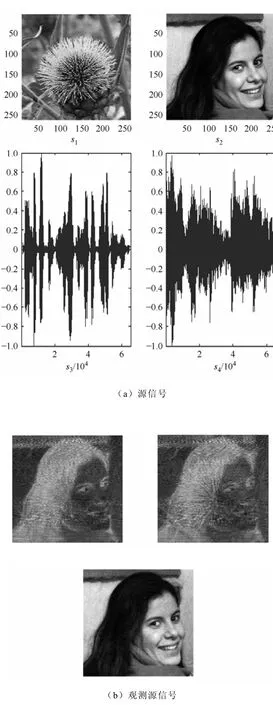
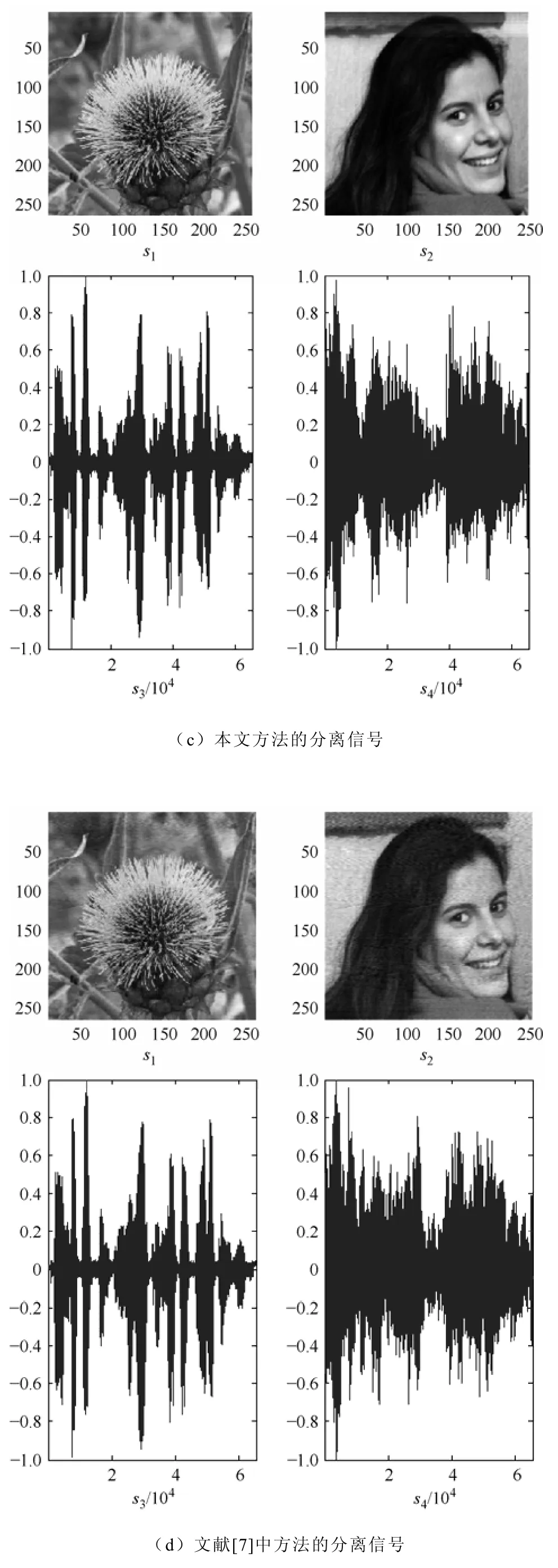
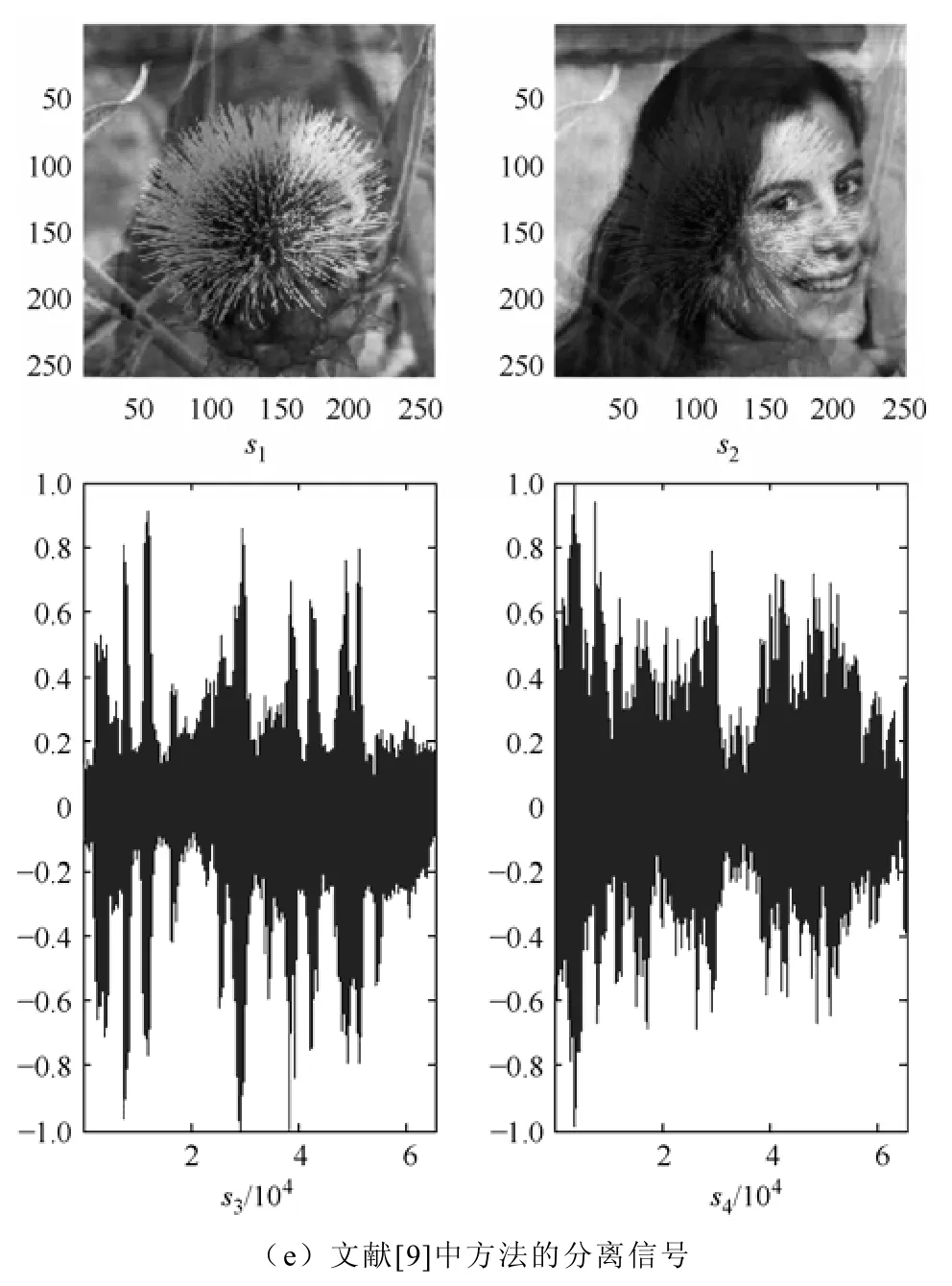
图3 不同UBSS方法的分离信号Fig.3 Separated signals of different UBSS methods

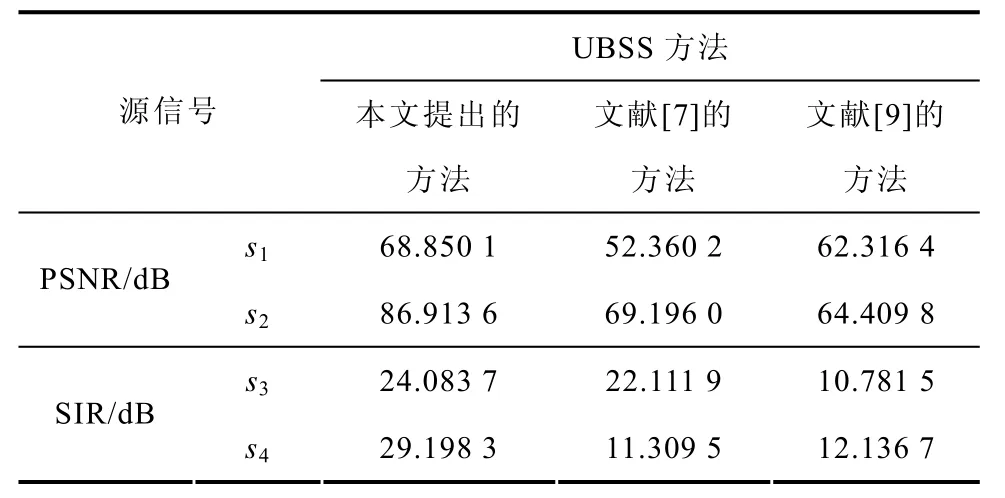
表3 不同UBSS算法分离结果的比较Tab.3 Comparison of results of different UBSS methods

由图2和表4的比较结果，本文提出的欠定盲源分离方法不仅能较好地分离出超高斯和亚高斯两种不同分布的源信号，同时它在源信号恢复的性能上也体现了它比其他方法更具有优越性。

5 结论

提出一种基于时域的欠定盲源分离方法，它不像传统的方法需要先在时频域上估算混合矩阵，再由优化算法恢复源信号，该方法首先采用一种基于差分峰度的盲抽取算法逐次分离欠定情况下的非平稳信号，然后再利用二阶统计量分离其余的源信号。仿真结果表明了该方法不仅能较好地分离出服从不同分布的源信号，同时它比其他传统方法具有更好的估计性能。

[1] Ohnishi N Y,Imiya A.Independent component analysis of optical flow for robot navigation[J].Neurocomputing,2008,71(10-12): 2140-2163.

[2] Hallez H,Vos M D,Vanrumste B.Removing muscle and eye artifacts using blind source separation techniques in ictal EEG source imaging[J].Clinical Neurophysiology,2009,120(7): 1262-1272.

[3] Nakajima H,Nakadai K K,Hasegawa Y.Blind source separation with parameter-free adaptive step-size method for robot audition[J].IEEE Transactions on Audio,Speech and Language Processing,2010,18(6):1476-1485.

[4] Dimitris G T,Aristidis C L,Nikolaos P G.Variational bayesian sparse kernel-based image deconvolution with student’s-t priors[J].IEEE Transactions on Image Processing,2009,18(4): 753-764.

[5] Aysal T C,Barner K E.Blind decentralized estimation for bandwidth constrained wireless sensor networks[J].IEEE Transactions on Wireless Comunications,2011,7(5): 192-202.

[6] Lü Q,Zhang X D.A unified method for blind separation of sparse sources with unknown source number[J].IEEE Signal Processing Letter,2006,13(1): 49-51.

[7] Yimaz O,Rickard S.Blind separation of speech via time-frequency masking[J].IEEE Transactions on Signal Processing,2005,52(7): 1830-1847.

[8] Bofill P,Zibulevsky M.Underdetermined source separation using sparse representation[J].Signal Processing,2001,81(11): 2353-2362.

[9] Khor L C.Robust adaptive blind signal estimation algorithm for underdetermined mixture[J].IEE Proceedings on Circuits,Devices and Systems,2006,153(4): 320-331.

[10] Snoussi H C,Idier J.Bayesian blind separation of generalized hyperbolic processes in noisy and underdeterminate mixtures[J].IEEE Transactions on Signal Processing,2006,54(9): 3257-3269.

[11] Liu W,Danilo P M.A normalized kurtosis-based algorithm for blind source extraction from noisy measurements[J].Signal Processing,2006,86(7):1580-1585.

[12] Cruces-alvarez S A,Cichocki A,Amari S.From blind signal extraction to blind instantaneous signal separation:criteria,algorithm and stability[J].IEEE Transactions on Neural Network,2004,15(4): 859-873.

[13] Hyvarinen A,Oja E.A fast fix-point algorithm for independent component analysis[J].Neural Computation,1997,19(7): 1482-1492.

[14] Deville Y,Benali M,Abrard F.Differential source separation for underdetermined instantaneous or convolutive mixtures: concept and algorithms[J].Signal Processing,2004,84(10): 1759-1776.

[15] Thomas J,Deville Y,Hosseini S.Differential fast fixed-point algorithms for underdetermined instantaneous and convolutive partial blind source separation[J].IEEE Transactions on Signal Processing,2007,55(7): 3717-3729.

[16] 史习智.盲信号处理[M].上海: 上海交通大学出版社,2006.

[17] 丁玉美,阔永红,高新波.数字信号处理——时域离散随机信号处理[M].西安: 西安电子科技大学出版社,2002.

[18] Ola F,Magnus B,Peter L.Exploratory fMRI analysis by autocorrelation maximization[J].NeuroImage,2002,16(2): 454-464.

[19] Wang R J,Zhou H F.Application of SVM in fault diagnosis of power electronics rectifiers[C].8th World Congress on Intelligent Control and Automation,2008: 1256-1260.

[20] Zhang H J,Shi Z W,Guo C H.Blind source extraction based on generalized autocorrelations and complexity pursuit[J].Neurocomputing,2009,72(10-12): 2556-2562.

[21] Cichocki A.Available: http://www.bsp.brain.riken[OL].jp/IC- ALAB/ICALABSignalProc/benchmarks.