盲源分离技术在振动法检测变压器故障中的应用

郭 俊 汲胜昌 沈 琪 祝令瑜 欧小波 杜利明

（1.西安交通大学电力设备电气绝缘国家重点实验室 西安 710049 2.河南省电力公司郑州供电公司 郑州 450000）

1 引言

在电力系统的各种设备中，电力变压器是比较昂贵且重要的枢纽设备，其运行的可靠性直接关系到整个电力系统的安全与稳定。电力变压器的历年统计资料表明，绕组与铁心是发生故障较多的部件[1]，积极开展这两个组件的状况检测和诊断，以便及时发现故障隐患，不但可以减少运行成本，延长设备寿命，而且能够预防变压器突发事故的发生，带来良好的社会和经济效益。

传统的频率响应法以及短路电抗法主要在变压器离线的条件下对绕组状况进行检测，而振动信号分析法不仅可以同时诊断绕组和铁心状况，而且与整个电力系统无电气连接，可方便、安全可靠地实现带电检测，因此振动法在近些年来一直是国内外研究的热点[2-12]。变压器油箱表面的振动由其内部多处振源所产生的振动混叠而成，且各振源振动产生的机理及相应的振动特性也不尽相同，而传统方法如傅里叶变换、小波变换[6]、HHT变换[5]都是直接在混叠信号上加以分析，不能准确地判断故障发生的部位，这给变压器故障特征识别和诊断带来了一定的困难。通常利用空载运行变压器的方法得到铁心振动信号，进而从负载运行时测得的振动信号中分离出绕组的振动信号，显然这种方法需要变压器空载运行，这在带电检测时是较难实施的。为此，文献[7,8]中提出了分离绕组与铁心振动信号的负载电流法，但这种方法需要积累不同负载电流下的振动数据，实施起来比较费时，无法在短时间内实现绕组与铁心振动数据的分离，且分离出的结果均只包含振动信号的基频分量，而忽略了含有大量信息的其他频率部分。

为解决上述问题，本文提出了基于盲源分离技术的变压器振动信号分析方法。盲源分离是指多个独立源信号共同传播时，在不需要了解传递通道的情况下，从混合信号中分离出各个振动源信号的一种方法[13]，可为设备的故障特征识别提供条件，已在混叠振动信号的分析中得到了广泛应用。最简单也是最普遍的盲源算法是对混合信号X(t) 进行独立分量分离（Independent Component Analysis，ICA），这种算法是基于源信号相互独立这个前提来进行分离的，如文献[14]中利用ICA算法对GIS局放信号进行了检测分离，这是因为超高频法检测到的不同位置处的局放信号是彼此相互独立的。但本文所涉及的变压器绕组和铁心振动信号，相互之间并不是完全独立的，存在频率上的混叠现象，因此ICA算法并不适用。为此，本文采用了一种改进的盲源分离算法，即子空间独立分量分离法（Sub-Band Decomposition Independent Component Analysis,SDICA），可以分离并不完全独立的源信号，且具有良好的应用效果。

本文首先分别介绍了基于ICA算法和SDICA算法的盲源分离技术，并利用仿真信号对这两种算法在变压器振动信号分离中的适用性进行了分析；然后基于测得的试验变压器的振动信号，对SDICA算法的影响因素及分离效果进行了研究。最后，本文将SDICA算法应用于一台现场运行的电力变压器的振动信号分离中，并分析了其诊断结果。这对于振动信号分析法在变压器绕组及铁心故障诊断中的推广应用具有重要意义。

2 变压器振动信号盲源分离算法

2.1 变压器油箱振动的振源

变压器油箱表面的振动通常是由铁心和绕组所产生的振动经过油和箱体的传递、混叠而成的。其中，绕组振动主要是来自绕组流过电流时在其本身所产生的电动力，与电流的平方成正比，且几乎全部的频谱分量都集中在基频100Hz处[2]；铁心振动主要来自于铁心的磁致伸缩以及硅钢片接缝和叠片中间的漏磁所产生的电磁力，由于存在磁滞效应，电动力与所施加电压的平方并不是线性关系。铁心振动信号的基频也为100Hz，但是在100Hz倍频处（甚至在一些50Hz倍频处）还存在着较大的分量，这正是铁心与绕组振动的最大区别。除此之外，还有一些产生振动的源头，如分接开关的操作、有可能发生的局部放电以及冷却系统的振动等。但是由于本文所研究的振动都是周期性的振动，而分接开关所产生的振动是暂态且非周期性的，可以不必考虑其影响；至于潜在的局部放电所产生的影响，由于其振动频带要远高于铁心和绕组的振动频带（集中于1 000Hz以下），也可不予考虑；而变压器的冷却系统，如油泵、风扇等，产生的振动信号集中在小于100Hz的低频段[2]，不会影响到变压器绕组及铁心振动信号的检测。因此，对于油箱表面的任意一点，其振动主要来源于两个方面，即：绕组和铁心。

2.2 盲源分离算法

2.2.1 ICA算法

ICA盲源分离算法是指在源信号未知的前提下，对混合信号进行线性变换，使得变换后的信号和源信号具有相同的波形。假设源信号为S(t)，各分量之间互相独立，观测到的混合信号为X(t)

式中，A为混合矩阵，为了简单起见，式（1）中X(t) 和S(t) 中的分量个数是相等的，这种情况下A即为一个方阵。

ICA算法的目的是找到另一个方阵W，使得

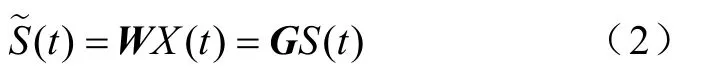
式中，W称为分离矩阵；G称为全局矩阵，G=WA；S˜(t) 即为最终的分离信号，具有与源信号S(t) 相等的广义形式。

ICA的核心内容是使得分离结果达到最大程度的不相关，根据对不相关性的量化标准的不同，也有着很多种不同的ICA算法，量化标准包括高阶统计量、互关联准则或者计算信号之间的熵值等。为了达到更高的计算和收敛效率，文献[15]中介绍了一种快速ICA算法，即快速独立分量分离（fastICA）算法。fastICA算法的核心内容是对分离矩阵W的每行分别进行估计，以计算第p行为例简单说明其算法步骤如下：

步骤1：对混合信号X进行白化，使得其满足

步骤2：设定分离矩阵第p行即wp的初始估计wp(1)，使其满足

步骤3：通过递推公式对wp进行进一步估计，递推公式为

式中，g为一个非二次函数，g′为其一次导数，g通常为

步骤4：对所得到的wp(k+1) 进行正交处理，为

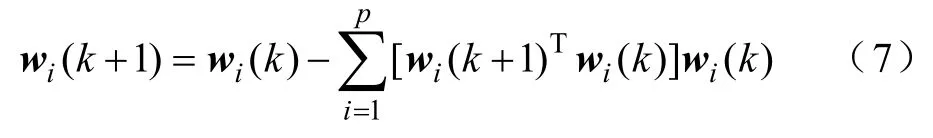
步骤5：对其进行归一化处理

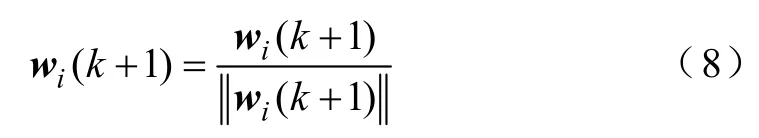
步骤6：比较wi（k+1）与wi（k），若其两者相差很大，重复步骤3～5，若两者已基本相等，说明算法已经收敛，停止计算。wi(k+1) 就是最终的wi。

由于fastICA算法的高效性和稳定性，正越来越多地被应用于源信号相互独立情况下的工程实际计算[16]，如图像处理或者信号识别等中。

2.2.2 SDICA算法

但在更多的领域当中，ICA算法的前提假设并不能很好地满足，即各源信号之间可能存在着一定的相关关系，例如本文所研究的绕组和铁心振动信号，在基频处和一些高频处是相关的，对于这种更为普遍的情况，fastICA算法的分离结果是不能令人满意的。对于这个问题，近些年一些学者提出了分离相关信号的各种方法[17,18]，其中应用最广泛的一种就是SDICA算法。

SDICA算法是基于源信号S(t) 由多个子空间Si(t) 构成（i=1,2,3,…,L），即

假定Si(t) 各信号之间在大部分区域是相关的，但是在另外一些很小的区域内不相关或者相关度很小。假设源信号S(t) 存在独立子空间Sn(t)，其中1≤n≤L，跟据ICA算法则有

式中，Xn(t) 为源信号中的独立子空间经过混合后在混合信号中所形成的子空间。这样来说，如果找到Xn(t)，通过

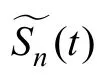
为了找到Xn(t)，引入线性函数Tn

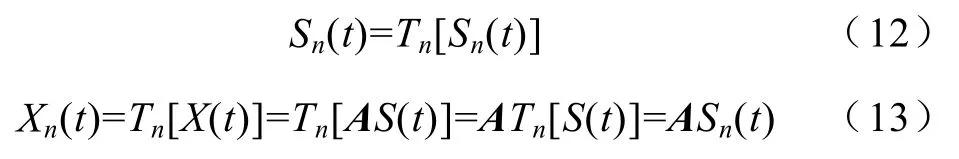
式中的Tn可看作是一个线性的滤波器，式（13）说明了信号中的独立子空间经过混合后在混合信号中依然是独立的子空间，也就是说混合信号中的独立子空间就是要得到的Xn(t)。基于此，可以通过先求得混合信号中的独立子空间，再对其进行fastICA计算，求得分离矩阵W。

子空间的分离方法有很多种，如采用高通滤波器[17]，这是基于对源信号的先验知识判断信号的高频部分更加独立，并不能对所有信号都适用；又如可采用一种基于互信息的自适应滤波器[18]，缺点是计算比较麻烦。本文采用的是小波包分解，应用较为成熟，且计算简便。

对于独立子空间的选取标准，本文采用互信息最小化准则，信号之间的互信息值（mutual information）MI定义如下[19]

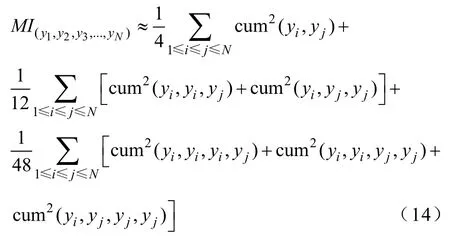
式中，cum() 表示信号的高阶统计量。

为了简单起见，本文所涉及的分离计算只选取两路混合信号进行分离。这样，对于本文两源两观测系统来说，只要求其2阶统计量即可。

另外，由于混合矩阵的未知性，对混合信号进行盲源分离会带来一个普遍性的问题，即分离结果的幅值和信号相互之间的顺序是不确定的，近些年一些学者对这一问题做出了一系列的研究，针对顺序改变的问题已经得到了很好的解决[20]，但是针对幅值改变的问题还需要再进行一定的研究。而在本文所讲述的盲源分离算法在变压器振动信号分离的应用中，由于铁心和绕组的振动信号特性相对较为明显，可直接对其进行识别；另外振动信号的波形中包含了丰富的信息，可以直接进行故障判断。

总的来说，本文所采用的SDICA盲源分离算法可以分为以下几个步骤：

步骤1：对信号进行小波包分解。

步骤2：对小波分解后的信号各子空间计算其MI值。选出MI值最小的一个或几个子空间，即为相对独立的子空间，并重构这几个子空间。

步骤3：将重构所得的信号进行fastICA分解，求得分离矩阵W。

步骤4：混合信号左乘分离矩阵W即为分离得到的源信号S˜(t)。

3 盲源分离算法的仿真验证

以下将根据变压器铁心和绕组的振动特性来构建模拟的振动信号，并对构建得到的信号进行任意混合，然后应用SDICA分离算法对其进行分离。为了检验分离效果，本文采用了两种检验标准。

（1）Amari误差率，定义如下：

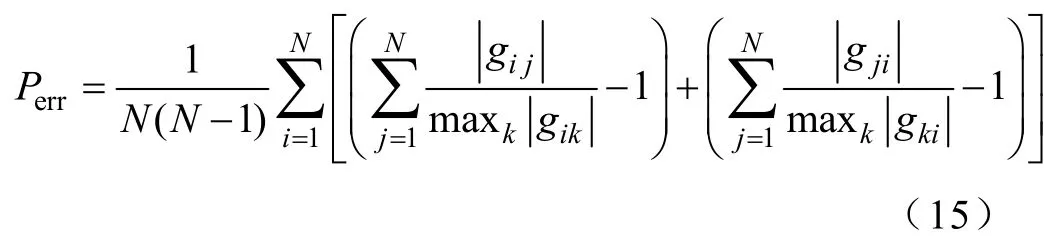
式中，gij=[G]ij；G为全局矩阵，G=WA。

误差率0≤Perr≤2，数值越小代表分离效果越好，即分离信号越接近于源信号；当Perr=0时，代表分离信号与源信号完全相等。

（2）信号波形相似系数。两列长度为K的信号波形相似系数定义如下

式中，λij表示信号yi与sj之间的相似关系，其值0≤λ≤1，数值越大代表波形相似程度越高，当λ=1时，表示两信号的波形完全相等。

波形相似系数矩阵M定义如下

为了验证SDICA算法在铁心和绕组振动信号分离方面的效果，先对铁心和绕组振动信号进行模拟，数学模型如式（18）、式（19）所示[2]。其中，考虑到铁心振动信号的非线性，式（19）的铁心信号中包含了一定的50Hz倍频信号

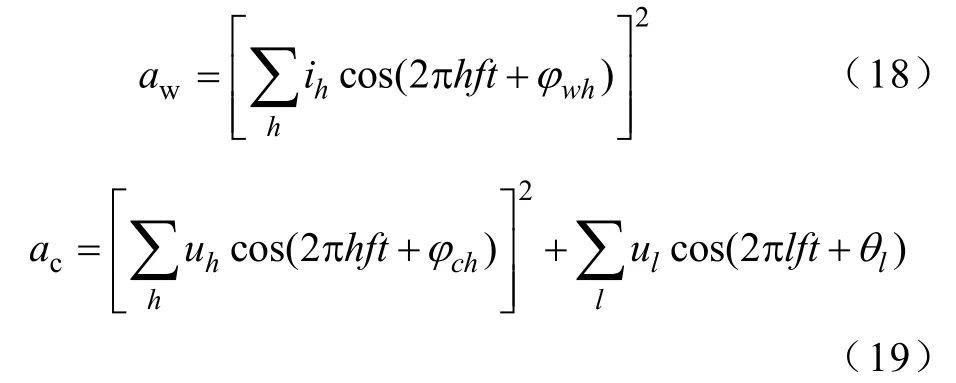
式中，aw、ac分别表示绕组和铁心振动信号；ih、uh、ul分别表示h和l次谐波时的电流和电压幅值；φ和θ表示初相角。

根据以上模型，建立绕组和铁心振动的模拟信号，如图1所示。

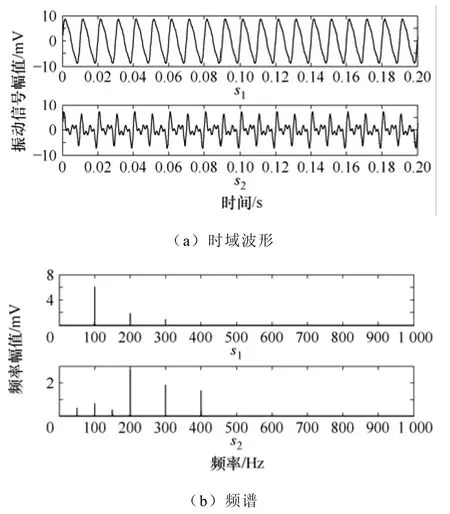
图1 仿真信号（s1与s2分别为绕组与铁心振动信号）Fig.1 Simulated signals (s1 and s2 is winding and core vibration signal respectively)

随机的设定6组混合矩阵，将源信号进行混合得到混合信号

以第一组混合矩阵A1为例来进行计算，混合后的信号如图2所示。

（a）时域波形

（b）频谱

由图2可以看到，混合后的两个信号波形十分相似。频谱方面也差别不大，如果这就是采集到的变压器油箱表面的信号的话，很难对铁心和绕组的具体情况进行分析。

针对上述情况，为了得到源信号，先采用传统的fastICA算法来对混合信号进行盲源分离，得到的结果如图3所示。

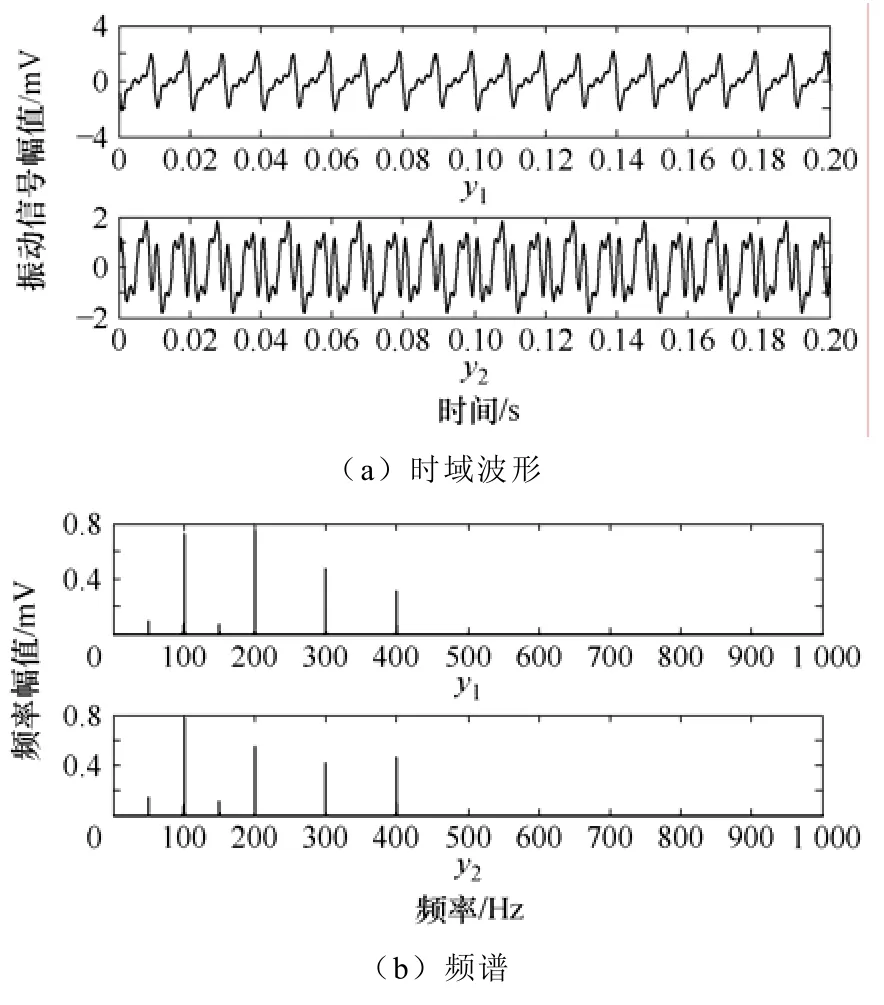
图3 fastICA分离结果（y1与y2分别为分离后的绕组与铁心振动信号）Fig.3 Separated signals with fastICA (y1 and y2 is the winding and core vibration signal after separating respectively)

与源信号进行对比可以看到，分离后的信号在一定程度上恢复了源信号，但是频谱方面仍有较大的差别，计算误差率Perr和波形相似系数矩阵M，分别得到

由结果可以看出，Perr＞＞0，y1与s1，y2与s2的相似系数分别为0.785 2和0.830 6，均说明算法仅在一定程度上分离出了源信号，但是分离效果并不理想，如果应用在变压器绕组和铁心的状态监测方面，必然会对状态的准确判断造成一定的影响。为了得到更加准确的源信号，对混合信号运用SDICA算法进行分离。

先对信号进行1～5层的小波包变换，得到混合信号在各自对应的不同子空间处的MI值如图4所示。

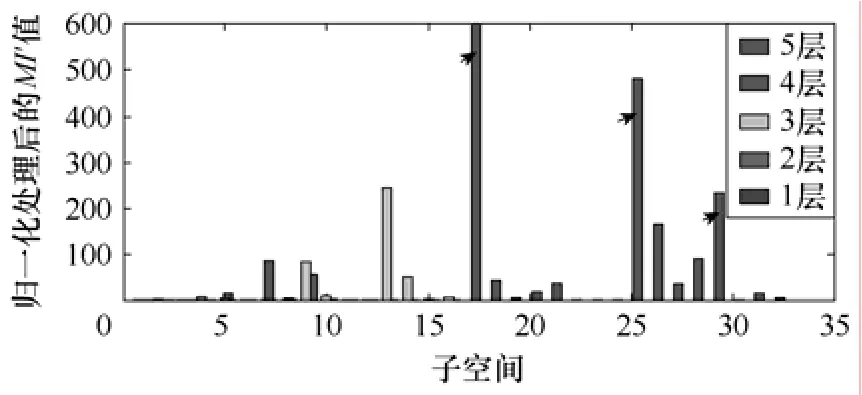
图4 混合信号各子空间的MI值Fig.4 The MI values of sub-bands of mixture signals

为了能更直观的找到MI值最小的子空间，图4中的数据经过了如下的归一化处理

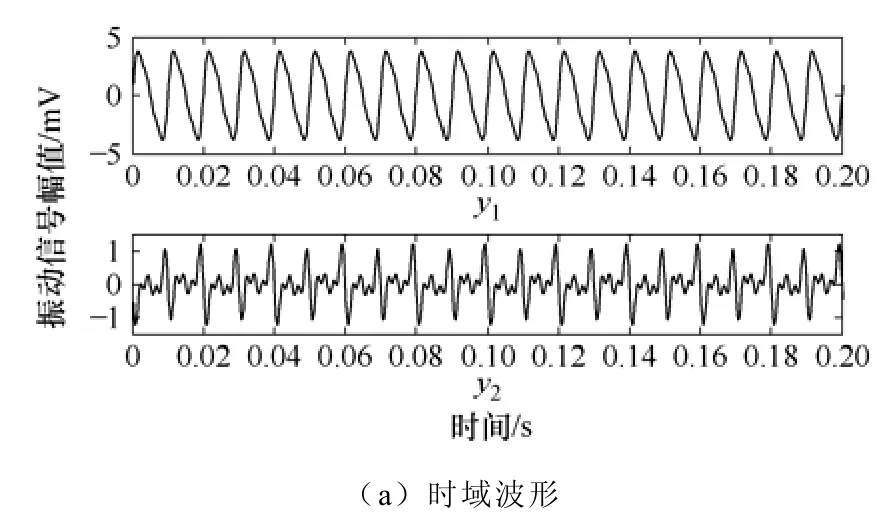
图5 SDICA分离效果（y1与y2分别为分离后的绕组与铁心振动信号）Fig.5 Separated signals with SDICA ( y1 and y2 is the winding and core vibration signal respectively)

从图5中可以看到，无论是时域波形还是频谱形状，分离信号与源信号均基本相同，再次计算误差率Perr和相似系数矩阵M，分别得到

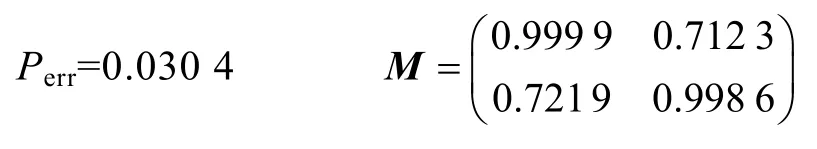
对另外5组混合矩阵分别用SDICA和fastICA算法进行分离，得到的误差率Perr和对应信号之间的波形相似系数如图6所示。

由图6可以看出，在将源信号任意混合的6组试验中，SDICA分离结果的误差率Perr基本保持在0.1以下，分离信号与源信号之间的波形相似系数基本保持在0.9以上，均比fastICA算法的结果更好。这说明SDICA算法比fastICA算法更适用于源信号部分相关情况下的盲源分离，且可以有效的分离类似于绕组和铁心振动的混合信号。

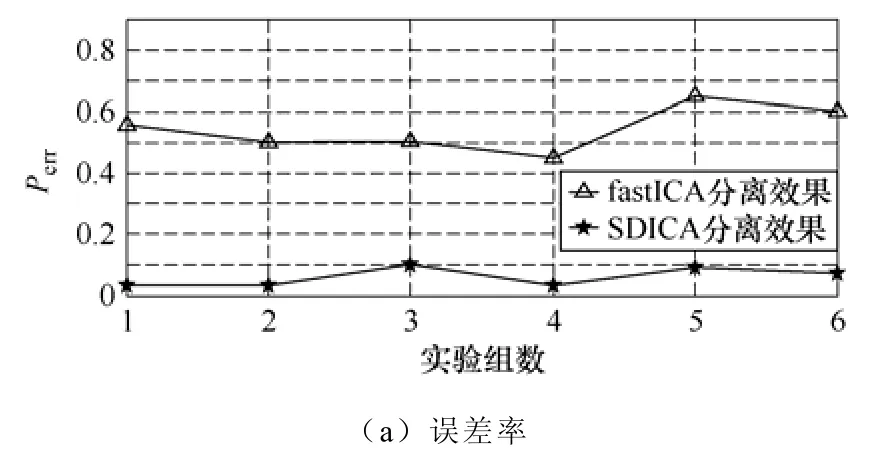
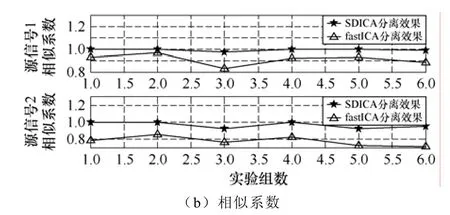
图6 各组实验分离效果Fig.6 Separating effect

4 盲源分离算法的实际应用

4.1 在试验变压器上的应用

为了检测算法分离实际变压器振动信号的效果，选取了一台试验变压器，测量变压器表面的振动信号，并应用SDICA算法进行分离。

实验中用到的测振仪器是激光测振仪，可以随时方便的改变测量位置，相比传统所用的压电式传感器最大的好处是不用贴在表面，对整个振动系统无附加影响。试验变压器型号为BVT/J，容量为2kVA，二次额定电压为20kV，电流为0.1A。所用负载为60Ω～200kΩ 可调电阻，功率0.6～2kW可调。测量位置选择了振动信号更为明显的中轴线上的上、中、下三个位置，分别记为1、2、3号，在测得信号后，可以任取其中的两路信号进行分离，总共有三种分离结果。实验接线图以及测量位置如图7所示。

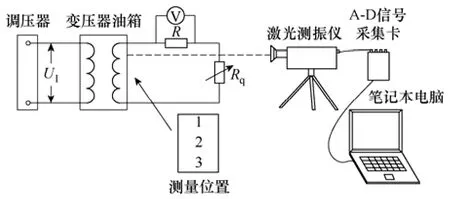
图7 实验接线图以及测量位置Fig.7 The experiment circuit and measured position

以负载为150kΩ，二次侧施加电压为9.5kV为例进行测量。在进行小波去噪后，测量所得的振动信号如图8所示。

由图8中可以看到，三个位置处的振动信号的频谱特性几乎是相同的，并不能直接拿来对铁心和绕组的振动做具体的分析。为了将两者的信号分别提取出来，对信号进行盲源分离。以位置1和3处的信号为例，分离得到的结果如图9所示。

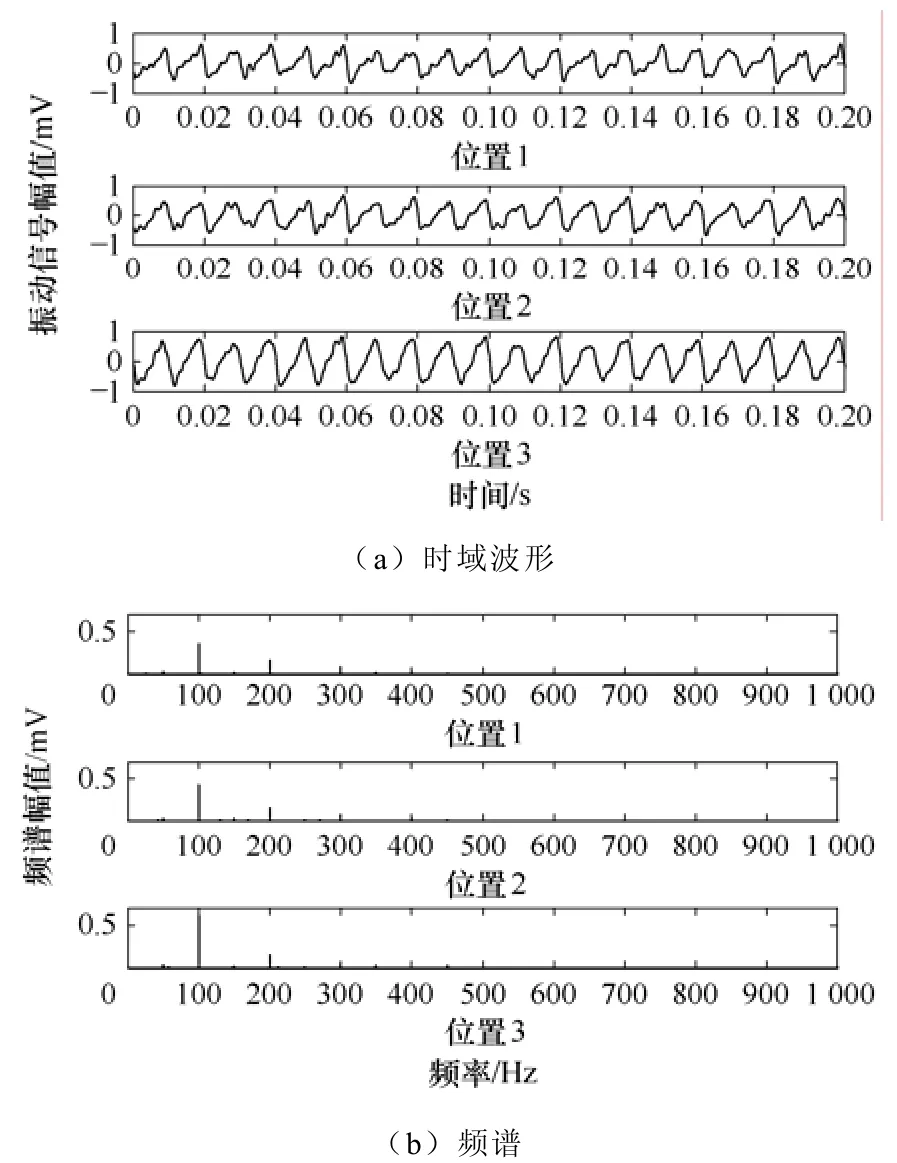
图8 实际振动信号图Fig.8 The vibration signals from test transformer

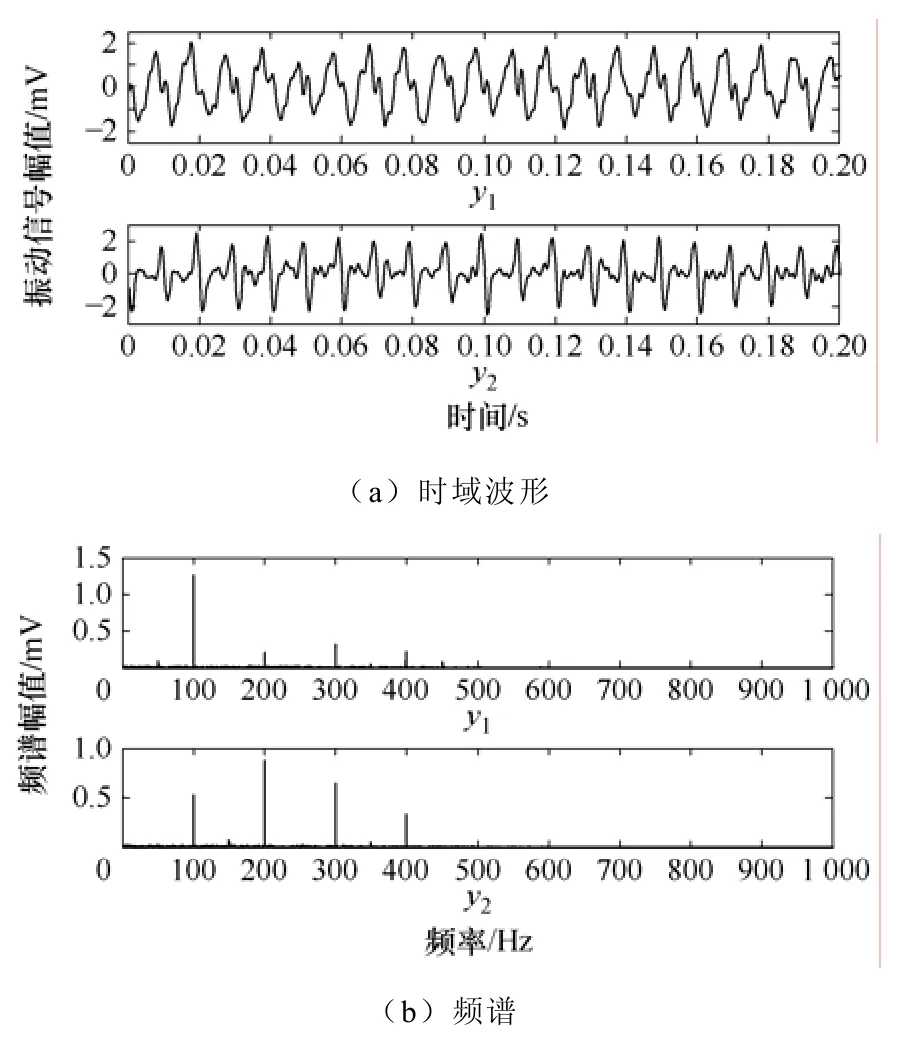
图9 分离效果（y1与y2分别为绕组和铁心信号）Fig.9 Separated signals (y1 and y2 is the winding and core vibration signal respectively)

由图9中可以看到，算法将两位置处的振动信号分离成为两个有着不同频谱特性的信号，分离信号y1的频谱特性与一般情况下的绕组频谱特征相类似，y2则与铁心振动特征类似。为了对其正确性进行检验，将变压器空载，并测量其在二次电压为9.5kV时三个位置处的空载振动。由于所测得的振动信号只是铁心振动经过内部传递在表面所形成的混合信号，并不等于其内部真实的铁心振动信号，故对所测信号按照一源三观测系统进行分离，得到的实际铁心振动信号如图10所示。

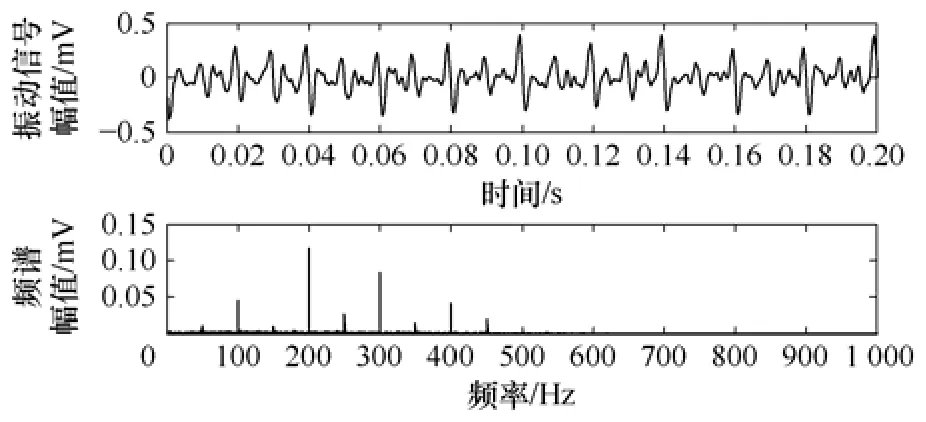
图10 铁心振动波形和频谱图Fig.10 The core vibration signal

将图10与图9进行比较可以发现，分离结果中的y2与铁心振动信号波形基本是一致的。计算y1、y2与铁心振动信号的波形相似系数，结果为：M1=[0.360 3,0.969 1]。y2与铁心振动信号的相似系数达到了0.969 1，说明其就是分离出的铁心振动信号，算法成功地将铁心与绕组信号分离开来。但正如前面所讲，两者的幅值并不相等，这是由于分离信号是源信号的广义相等形式，分离算法只能还原源信号的波形及频谱形状，并不能准确地还原幅值的大小。对于这一点，由于波形中包含了丰富的信息[5,6]，可以利用波形所包含的信息来进行故障判别。

为了验证不同位置处的分离情况，分别以1、2位置处和2、3位置处信号为源信号作分离计算，如果定义Ma为分离准确率，其值等于波形相似系数中较大值，即：

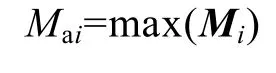
经计算，另外两组结果的分离准确率分别为：Ma2=0.9599和Ma3=0.9604，与第一组基本一致，说明测量位置的差异对分离结果不会产生较大影响。

为了检验所施加电压对分离结果的影响，保持负载不变，分别测量副边电压为9kV、8.5kV、8kV、7.5kV时的油箱表面振动信号，然后利用SDICA算法进行分离，并与空载下测得的振动信号比较，计算其分离准确率。由此得到，分离准确度与所施加电压的关系如图11所示。

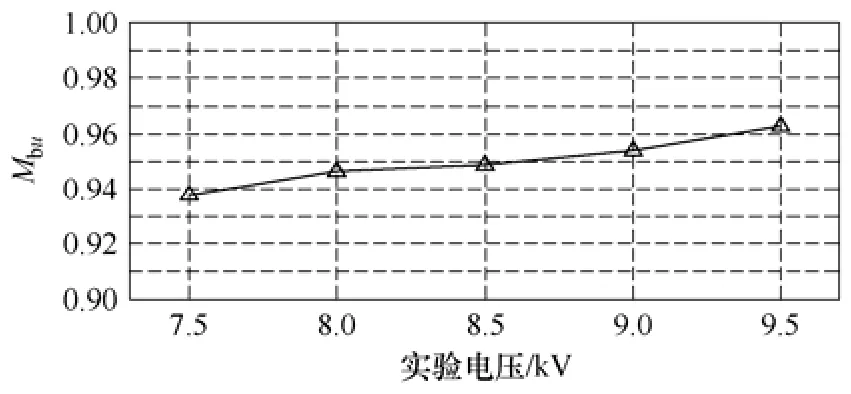
图11 分离准确率随实验电压的变化关系Fig.11 The separation precise versus experiment voltage

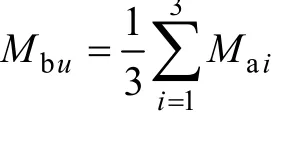
由图11中可以看出，分离准确率都保持在较高的水平，且随着电压的升高而略有升高，其原因主要是：在电压较低时，信号的有效分量较少，即使经过了小波去噪，但在低频段仍会残存有一定的噪声，会对信号的分离产生一定的影响；而在施加电压较高时，所得振动信号幅值较高，这样外界干扰相对就小，因此分离准确度有所提高。

为了检验所带负载的大小对分离结果的影响，将负载电阻在60～200kΩ 之间进行调节，每改变10kΩ 测量一组数据，在每个负载等级下，又分别测量在不同电压等级下的三个位置处的振动信号，分别将其分离，并与空载信号进行比较。定义负载为r时的分离准确率为Mr，其值等于负载为r时每个电压等级下分离准确率的平均值，即

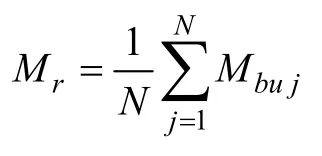
式中，N为电压等级的个数。

则得到Mr关于负载大小的变化关系，如图12所示。

图12 分离准确率随负载的变化关系Fig.12 Separation precise versus load

由图12可以看到，分离准确率随着负载的变化基本保持稳定，只是在阻值最小或最大的地方略有下降。这是由于阻值的大小直接反映了变压器中电压和电流的比值关系，也进一步反应了振动信号中铁心与绕组振动分量的比值关系，在负载过小的地方，绕组振动分量会偏小，而在负载过大的地方，铁心振动分量则会偏小，这会在一定程度上影响分离的效果。当然，由图12中可以看出，负载变化对其影响保持在一定的可接受范围内。

以上通过对试验变压器的分离实验，分析了振动测量位置、施加电压和所带负载对分离结果的影响，实验的结果表明这些因素会对分离结果产生一定的影响，但都维持在较小的水平。因此，SDICA算法可以有效的分离变压器绕组和铁心振动信号。

4.2 在现场电力变压器上的应用

为了检验分离算法在实际故障检测中的应用，对一台在运行中的存在安全隐患的变压器进行振动信号采集，并对其进行盲源分离。所测变压器为某水电站的一台500kV三相分离式的变压器，其中的C相曾发生过短路故障，并且未更换过绕组。为了与其进行对比，同时也采集A、B两相的振动信号，测量位置为试验变压器的1号和3号位置，所测得的信号经过小波去噪后如图13所示。

图13 实际电力变压器三相振动信号Fig.13 The vibration signals from power transformer

由图13可以看出，直接测量所得的信号非常杂乱，并没有很多直接的有用信息，C相信号也没有很明显的故障特征，难以对该变压器状态进行判断。为了分别观察绕组和铁心的振动信号，对所测信号进行分离，得到如图14所示的结果。

由图14中的A、B两相结果可以看出，分离信号中的y1信号为绕组振动信号，y2则为铁心振动信号。将A、B两相与C相分离结果进行比较可以发现，C相的铁心信号与A、B两相差别不大，而C相绕组信号相比前两相则出现了明显的高频分量，这与实际变压器的运行情况是相符的。由于C相绕组曾发生过短路故障，绕组在短路冲击力的作用下可能发生了一定的形变，这会导致其振动中增加很多高频成分[4,9,11,12]。可见分离算法将包含有明显故障分量的绕组信号与铁心信号成功地分离开来，并且由分离结果可以很清楚地判断出故障发生的位置。

图14 分离信号图：y1与y2分别为绕组和铁心振动信号Fig.14 Separated signals ( y1 and y2 is the winding and core vibration signal respectively)

5 结论

振动法检测变压器故障具有在线、灵活、安全等特点，但是在实际应用中，其检测到的信号是绕组和铁心振动信号的混合，无法对其信号进行单独的分析，可能会对故障的判断带来干扰。正是基于此情况，本文通过仿真以及实验室实验和现场实验证实了SDICA算法可以有效的分离绕组和铁心振动信号，并且分离的结果基本不受测量位置、电压等级以及负载大小的影响，使得分别对绕组和铁心振动信号的故障特征进行研究并初步判断故障发生部位成为可能。

需要说明的是，在实际变压器故障检测中，要实现最终的对绕组和铁心故障信息的判断以及识别，还需要研究很多内容。首先，本文验证了不同测量位置、电压等级和负载大小基本不会影响分离效果，而在变压器绕组发生变形时，对于不同的变形方式和变形程度，油箱表面的振动也各不相同，在实际检测时其是否会影响到分离效果还需要通过进一步的验证。其次，本文研究了变压器绕组和铁心振动信号的盲源分离方法，而要最终实现对变压器故障的识别和故障判据的建立，还需要在对振动信号盲源分离的基础上分别研究绕组和铁心振动信号的故障特征，识别其各自的故障类型，建立故障数据库。最后，利用盲源分离算法分离变压器振动信号可以大致的判断故障发生的部位，例如在单相变压器中，由于绕组和铁心振动特征的不同，在发生故障时可以由此大致判断是绕组故障或铁心故障；又或者在三相一体式变压器中，由于其每相绕组的振动相位不同，所以当其中的某一相绕组发生故障时会在油箱表面表现出其独特的振动特性，也可根据此来大致的判断故障发生于哪一相绕组。但是由于变压器绕组和铁心振动信号都是周期信号，其故障信号一般也为周期信号，所以目前很难对其具体的故障发生位置进行定位，问题的解决同样需要盲源分离算法的进一步发展。在本文中，主要关注了变压器绕组和铁心振动信号的盲源分离方法，使得可以初步分离其二者的相关信号，而对具体故障信息的识别和判断还需要在以后的工作中在大量积累现场实测数据的基础上做更深入的研究。

[1] 王梦云,凌愍.大型电力变压器短路事故统计与分析[J].变压器,1997,34(10): 12-17.Wang M Y,Ling M.Statistics and analysis on short-circuit faults of large power transformers[J].Transformer,1997,34(10): 12-17.

[2] Belén G,Juan C B,Ángel M A.Transformer tank vibration modeling as a method of detecting winding deformations—part I: theoretical foundation[J].IEEE Transactions on Power Delivery,2006,21(1):157-163.

[3] Lavalle J C.Failure detection in transformer using vibrational analysis[M].MIT: Cambridge,1986.

[4] 谢坡岸,饶柱石,朱子述.大型变压器绕组有限元建模与分析[J].振动与冲击,2006,25(2): 134-137.Xie P A,Rao Z S,Zhu Z S.Finite element modeling and analysis on transformer windings[J].Journal of Vibration and Shock,2006,25(2): 134-137.

[5] 熊卫华,赵光宙.基于希尔伯特-黄变换的变压器铁心振动特性分析[J].电工技术学报,2006,21(8):9-13.Xiong W H,Zhao G Z.Analysis of transformer core vibration characteristics using Hilbert-Huang transformation[J].Transactions of China Electrotechnical Society,2006,21(8): 9-13.

[6] 汲胜昌,刘味果,单平,等.小波包分析在振动法检测变压器铁芯及绕组状况中的应用[J].中国电机工程学报,2001,21(12): 24-27.Ji S C,Liu W G,Shan P,et al.The application of the wavelet packet to the monitoring of the core and winding condition of transformer[J].Proceedings of the CSEE,2001,21(12): 24-27.

[7] 汲胜昌,李彦明,傅晨钊.负载电流法在基于振动信号分析法监测变压器铁心状况中的应用[J].中国电机工程学报,2003,23(6): 154-158.Ji S C,Li Y M,Fu C Z.Application of no-load current method in monitoring the condition of transformer’s core based on the vibration analysis method[J].Proceedings of the CSEE,2003,23(6): 154-158.

[8] Ji S C,Luo Y F,Li Y M.Research on extraction technique of transformer core fundamental frequency vibration based on OLCM[J].IEEE Transactions on Power Delivery,2006,21(4): 1981-1988.

[9] 冯永新,邓小文,范立莉,等.大型电力变压器振动法故障诊断的现状与趋势[J].南方电网技术,2009,3(3): 49-53.Feng Y X,Deng X W,Fan L L,et al.Status and trend of large power transformer’s fault diagnosis with the vibration method[J].Southern Power System Technology,2009,3(3): 49-53.

[10] 洪凯星,潘再平,黄海.短路条件下变压器振动特性研究[J].机电工程,2010,27(6): 87-90.Hong K X,Pan Z P,Huang H.Research on short circuit vibration of power transformer[J].Journal of Mechanical & Electrical Engineering,2010,27(6):87-90.

[11] 唐卫民,傅坚,邵宇鹰,等.大型变压器绕组状态振动分析法的试验研究[J].变压器,2010,47(1):25-27.Tang W M,Fu J,Shao Y Y,et al.Testing research on vibration analysis of large transformer winding[J].Transformer,2010,47(1): 25-27.

[12] 王世山,汲胜昌,李彦明.利用振动法进行变压器在线监测的应用研究[J].变压器,2002,39(1): 73-76.Wang S S,Ji S C,Li Y M.Application research on transformer on-line monitoring with vibration method[J].Transformer,2002,39(1): 73-76.

[13] Tong L,Inouye Y,Liu R.Waveform-preserving blind estimation of multiple independent sources[J].IEEE Transactions on Signal Processing,1993,41(7):2461-2470.

[14] Ju T,Wei L,Liu Y L.Blind source separation of mixed PD signals produced by multiple insulation defects in GIS[J].IEEE Transactions on Power Delivery,2010,25(1): 170-176.

[15] Aapo H.Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3): 626-634.

[16] 焦卫东,杨世锡,钱苏翔,等.联合应用MUSIC与FastICA算法实现多个时空混叠源信号的波形重建[J].机械工程学报,2010,46(6): 63-70.Jiao W D,Yang S X,Qian S X,et al.Waveform reconstruction of multiple spatio-temporal mixed sources by the joint use of MUSIC and FastICA[J].Journal of Mechanical Engineering,2010,46(6):63-70.

[17] Cichocki A.General component analysis and blind source separation methods for analyzing multichannel brain signals[C].Statistical and Process Models of Cognitive Aging,2007; 320-329.

[18] Zhang K,Chan L W.An adaptive method for sub-band decomposition ICA[J].Neural Comput,2006,18(2): 191-223.

[19] Cruces S,Castedo L,Cichocki A.Novel blind source separation algorithms using cumulants[C].IEEE International Conference on Acoustics,Speech,and Signal Processing,2000: 3152-3155.

[20] Ding S X,Huang J,Wei D M,et al.A near real-time approach for convolutive blind source separation[J].IEEE Transactions on Circuits and Systems—I:Regular Papers,2006,53(1): 114-128.