多输入多输出正交频分复用中基于频域的信干噪比估计

李志刚 刘 田 邵士海 唐友喜

（电子科技大学通信抗干扰技术国家级重点实验室，四川 成都 611731）

引 言

在多输入多输出正交频分复用（MIMO OFDM）［1］下行链路中，终端需要实时测量子载波上的信干噪比（SINR），尤其是在开环和闭环复用模式下，终端把测得的SINR反馈给基站端，供下行发射的调制编码方式选择参考。因此，SINR估计的准确性将直接影响系统性能，是无线通信系统进行资源分配的关键参数指标之一。

在现有的文献中，文献［2］和文献［3］分别针对时分多址和码分多址链路的时域SINR估计进行了讨论。针对OFDM链路，文献［4］利用时域相关性估计信噪比，该方法还有待扩展到MIMO OFDM系统中。文献［5］利用OFDM中循环前缀（CP）和部分载波信号的相关性，对噪声功率进行了估计，但该方法无法对其他载波上干扰信号的功率进行估计。文献［6］在MIMO OFDM场景下，分析了线性接收机（迫零或最小均方误差）中相位噪声对SINR估计误差的影响。文献［7］在平坦衰落信道中，提出了基于最大似然（ML）准则的SINR估计方法，在多载波情况下，随着子载波数量的增大，其计算量是常规器件无法承受的。

在频率选择性衰落信道中，针对MIMO OFDM的链路特征提出一种低复杂度的SINR估计方法：利用参考信号载波的频域相关性构造降秩矩阵，把其协方差矩阵分解为信号空间矩阵与噪声空间矩阵［8］之和，最后提取最小特征值来估计SINR。并且对SINR估计误差进行了理论分析及计算机仿真验证，结果表明：在SINR小于30dB时，该方法只需要利用连续4个参考信号载波，便可实现估计误差小于0.2dB.

如无特殊注明，采用以下标记：大写粗斜体A表示矩阵，其中第m行第n列元素为amn，大小写斜体表示变量，（·）＊表示（·）的共轭，（·）H表示（·）的共轭转置，diag｛·｝表示对角矩阵，「·」表示向下取整，E｛·｝表示数学期望，

1 信道模型与估计

考虑具有MT根发射天线和MR根接收天线的MIMO OFDM系统。系统带宽被分为N个子载波，循环前缀长度为Ncp.在某一时刻，在第k（k＝1，…，N）个子载波上的频域响应矩阵H（k）为

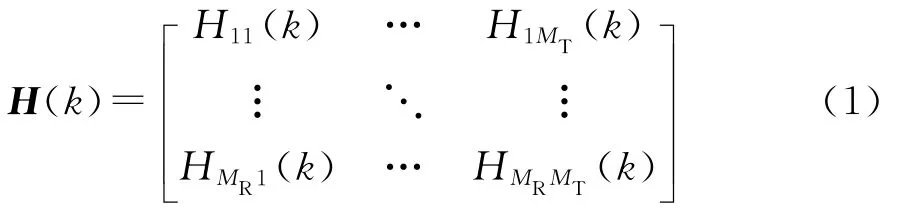
式中Hnm（k）表示在第k个子载波上由第m（m＝1，…，MT）根发射天线到第n（n＝1，…，MR）根接收天线的信道频域响应，即［9］

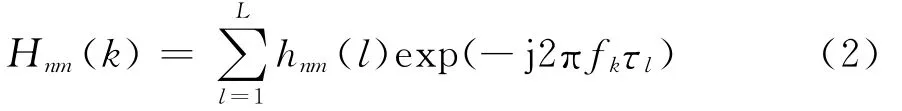
式中：L表示多径数；hnm（l）表示第m根发射天线到第n根接收天线之间第l条径的时域信道衰落系数，其服从均值为0、方差为的复高斯随机变量；τl表示第l条径的时延，l＝1，2，…，L；fk表示第k个子载波的载波频率。对于l＝1，2，…，L，假设hnm（l）之间是相互独立的，且满足信道功率归一化条件，即

为了估计信道矩阵（1），MIMO OFDM中采用在时域和频域上正交的参考信号序列［10－11］。设在频域上相邻参考信号的间隔为Df，在第k（k＝1，1＋Df，1＋2Df，…，1＋（M－1）Df）个子载波上插入参考信号，共插入M＝「N／Df」个参考信号，且参考信号的载波间隔Df满足信道相干带宽条件［9］：

式中：Δf表示子载波间隔；τmax表示最大多径时延。考虑信道估计存在误差，基于最小二乘（LS）信道估计，得到估计的信道矩阵H（k）为［12］

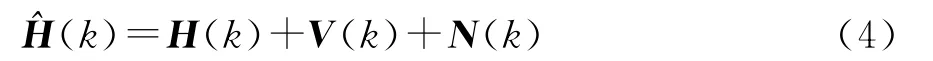
式中：V（k）表示干扰矩阵；N（k）为噪声矩阵。干扰信号源于运营商之间或不同制式之间造成的网络干扰，建模干扰矩阵中的元素为服从功率为的随机变量。建模噪声矩阵中的元素服从均值为0、方差为的加性复高斯随机变量。假设信道、干扰和噪声项之间相互独立。

2 信干噪比估计

考查在第n（n＝1，…，MR）根接收天线上的SINR估计，SINR估计步骤如图1所示。

考虑相邻的Nf（Nf≤M＝「N／Df」）个参考信号载波，Nf表示用来进行SINR估计的载波个数，其值的界定理论上是通过比较信号空间的最小特征值是否远远小于噪声空间的特征值，实际操作中可以依据实验结果部分图2的讨论分析来选取。在第p（p＝1，…，Nf）个参考信号载波上，从第m（m＝1，…，MT）根发射天线到第n（n＝1，…，MR）根接收天线之间的信道频域衰落系数记为Hnm（1＋（p－1）Nf）.对第n根接收天线进行SINR估计，其他接收天线的SINR估计可类似得出，为了叙述分析方便，不妨省略下标n以及省略表示数据信号的序号，Hnm（1＋（p－1）Nf）简记为（p）.利用载波之间的相关性，在接收端构造如下MT×Nf维降秩矩阵

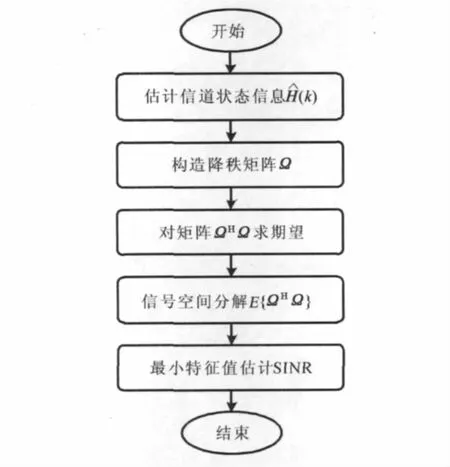
图1 SINR估计流程

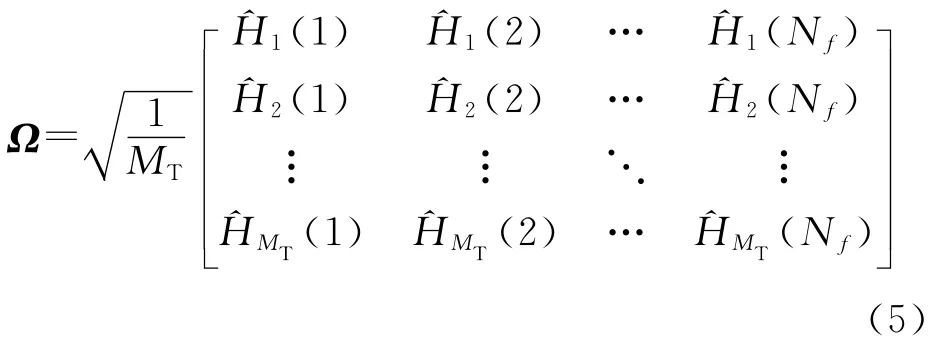
把Ω的协方差矩阵记为RΩ≜E｛ΩHΩ｝，RΩ的第（p，q）个（p＝1，…，Nf，q＝1，…，Nf）元素RΩ（p，q）为

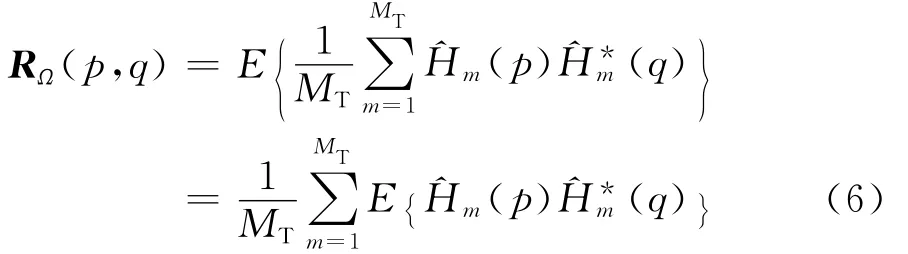
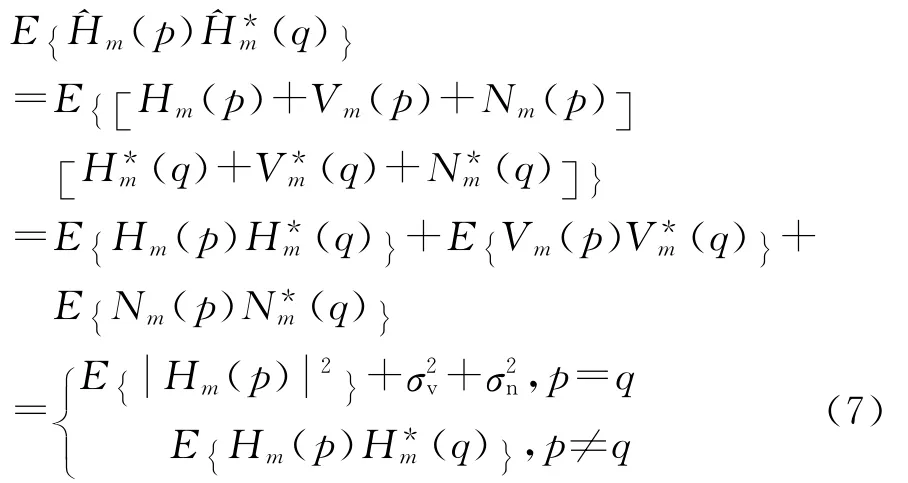
式中E｛（p）（q）｝化简为式（7）第二个等号成立是由于假设信道、干扰和噪声之间相互独立，以及信道和噪声的0均值特性。对式（7）中的E｛Hm（p）（q）｝进一步化简，有

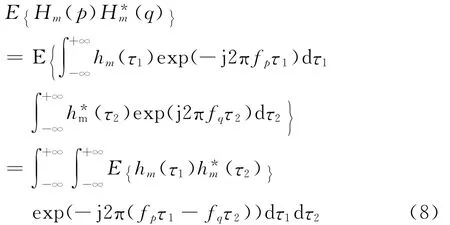
实际信道通常为广义平稳不相关散射（WSSUS）信道［13］，每根发射天线到接收端的信道衰落系数同分布，那么对任意m均有下式成立［13］：

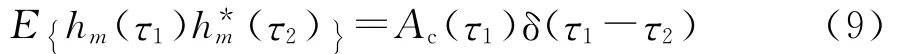
式中：Ac（τ）是信道的功率时延谱；δ（·）表示Dirac冲击函数。把式（9）代入式（8）得到

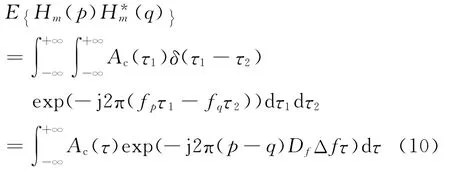
式（10）表示信号包络相关性与频率间隔的关系。把式（10）表示为离散形式，有

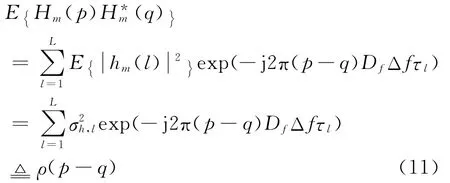
式中参数、Df、Δf和τl是已知参数，相关系数ρ（p－q）可以被确定。把式（11）代入式（7）得到

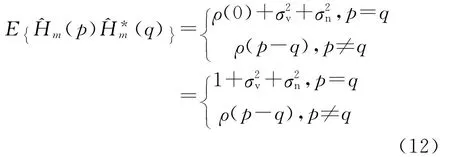
把式（12）代入式（6），得到Ω的协方差矩阵

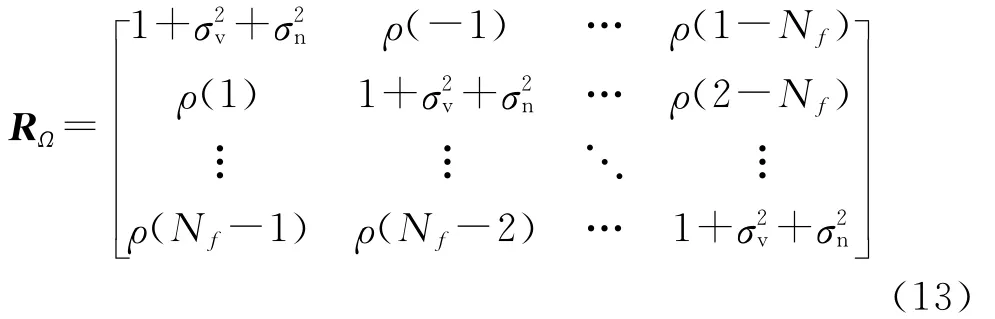
下面对RΩ进行信号空间分解，通过提取RΩ的最小特征值来估计SINR.定义矩阵

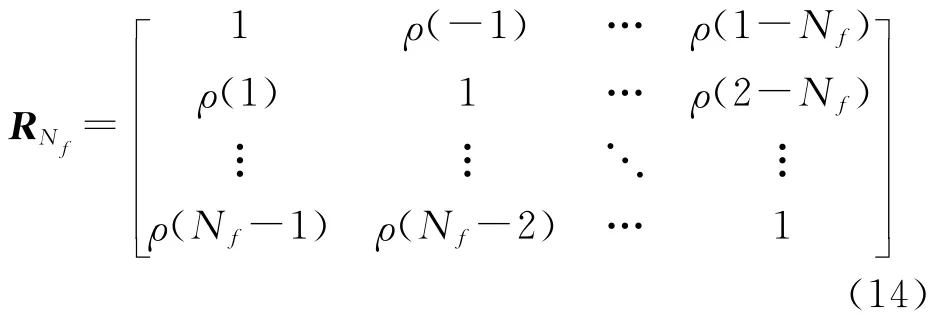
那么由式（13），RΩ可以表示为

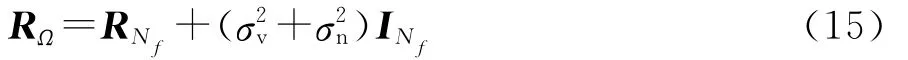
由式（15）可以看出，估计的信号空间矩阵RΩ可以分解为实际的信号空间矩阵和噪声空间矩阵＋之和。对矩阵进行特征值分解，设λi是矩阵的第i（i＝1，2，…，Nf）个特征值，Σ＝diag｛λ1，λ2，…，｝是由上述特征值组成的对角化矩阵，从而矩阵可以写为［14］

式中U是由特征值对应的特征向量组成的酉矩阵。由式（15），矩阵RΩ可以化为

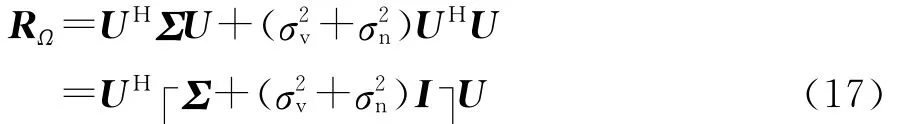
由于参考信号载波之间的相关性，矩阵相邻列向量之间具有一定的相关性，矩阵经奇异值分解后的特征值有大有小，列向量之间的相关性越强，特征值之间大小差距越明显，最小特征值会随着载波间相关性的增强趋于0，甚至有≪＋.另一方面，矩阵RΩ的最后一个特征值可以表示为与＋两项的和，而≪＋表明信号空间的最小特征值对噪声空间的特征值的影响很小，从而可以利用RΩ的最小特征值估计SINR.

综上，SINR估计步骤如下：首先，接收机对信道状态信息H（k）进行估计，选取连续Nf个参考信号载波的信道衰落系数组成降秩矩阵Ω.然后，求协方差矩阵RΩ＝E｛ΩHΩ｝.最后，通过特征值分解分离信号空间与噪声空间，提取矩阵RΩ的最小特征值来估计SINR.

从信号空间矩阵的表达式（14）看出表示参考信号经历的信道在频域上的相关性，该相关性与功率时延谱Ac（τ）有关，所提方法是利用该相关性来估计SINR.另一方面，信道在时域上的相关性由最大多普勒扩展决定与信道的时域相关性无关，从而所提方法避免了最大多普勒扩展对SINR估计的不利影响。同时也不受MIMO空间相关性的影响，所提方法同样也适用于MIMO相关空间条件下的SINR估计。

3 误差分析

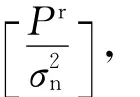
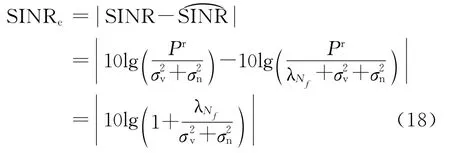
考查估计误差SINRe的性质。

首先，SINRe是大于零的。由于信号频率相关性函数（11）的绝对值小于1且单调递减［13］，易得Hermitian矩阵的所有主子式都大于零，则是正定矩阵。由于正定Hermitian矩阵的特征值都是正的［14］，得出的最小特征值＞0.又因为＋＞0，则lg＞0，由式（18）得出

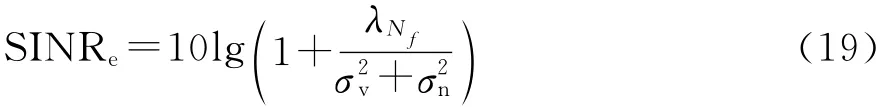
其次，SINRe随SINR的增加单调递增。式（19）又可以写为如下形式

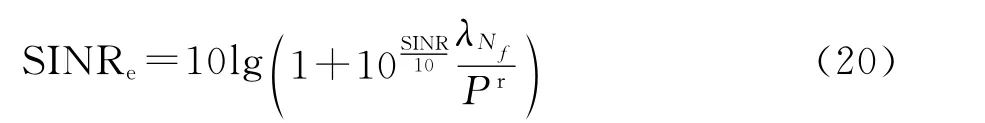
指数函数f（x）＝是单调递增的，对数函数g（x）＝lgx也是单调递增的。因为两个单调递增函数的复合函数h（x）＝lg 1＋也是单调递增的，（ ）且＞0，从而＝10lg （1＋）是关于SINR的单调递增函数，即SINR估计误差随着SINR的增加而增大。

SINRe随的减小而减小。当≪＋，即信号空间的最小特征值远远小于干扰与噪声功率之和时，估计误差SINRe≈0.

4 实验结果分析

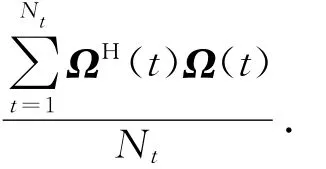
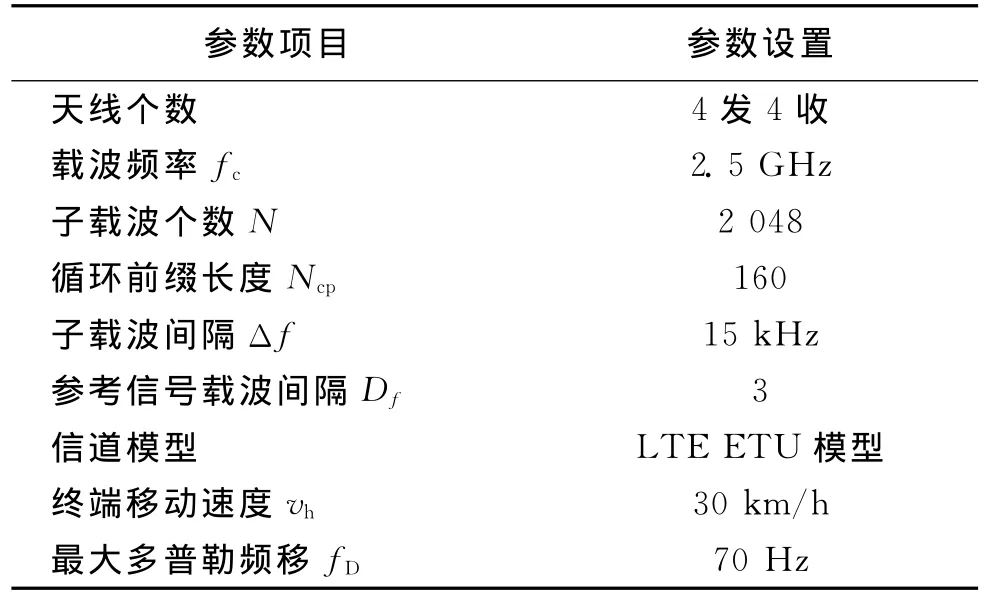
表1 系统参数

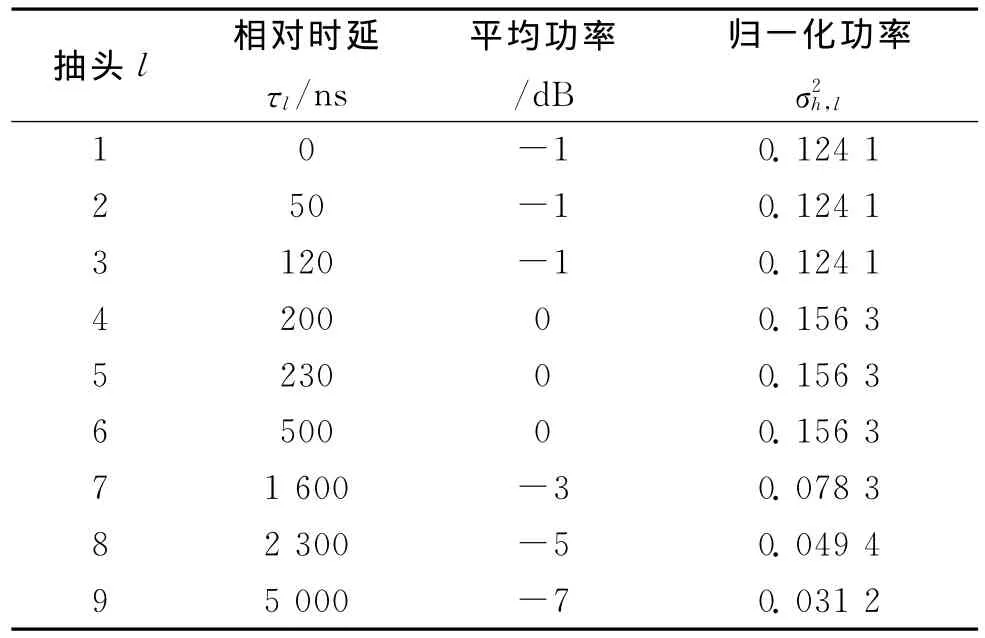
表2 LTE ETU信道模型

图2从理论上给出了在参考信号载波间隔Df不同情况下，信号空间（式（14））的最小特征值随连续导引载波个数Nf的变化情况。从图中可以看出：对于固定的导引载波间隔Df，当信号矩阵的空间维度Nf较小时，由于矩阵操作空间较小，信号空间的最小特征值与0有一定差距；当Nf增大后，既保证了原有各子载波的相关性，又使得操作空间增大，迫使最小特征值更趋于0，估计误差减小；当Nf较大时，最小特征值下降到某一平台。从图中还可以看出：随着参考信号选取密度的增加，信号空间各子载波的相关性增强，最小特征值收敛到0的速度会加快。从图2中也可以看出：在LTE规定的参考信号载波间隔Df为3和实际SINR＝30dB的条件下，当信号空间维度Nf≥4时，有10lg（）≪－40dB，可见对估计误差的影响很小，即使在高SINR条件下，本文方法对于SINR估计都具有良好的鲁棒性。

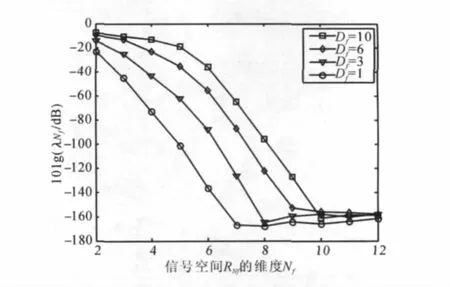
图2 信号空间的维度Nf对其特征值大小的影响

图3为所提SINR估计误差以及与文献［7］中ML方法的对比，其中信号空间维度Nf＝4，参考信号载波间隔Df为LTE协议规定的3，Nt表示时域上求期望的采样点个数。从图3看出：在理论上，当SINR小于15dB时，所提方法的估计误差与0接近；当SINR增加到30dB时，所提方法的估计误差约为0.2dB.在实际操作中，当统计点个数Nt＝103时，所提方法的估计误差与理论误差较为接近，两者之间的差值在图中最大处为0.1dB；随着统计点个数Nt增加到104时，统计平均结果与理论期望结果更趋于一致，两者之间的差值在图中最大处不超过0.03dB.并且所提方法与文献［7］中的ML方法进行了对比，在Nt个数相同以及低SINR条件下，所提方法的估计误差性能略差于ML方法。如果实际的SINR更高（大于30dB），所提方法与ML方法的性能差距会明显增大。为了减少差距，可以根据图2选择更大的Nf，使得足够小，这样可以保证所提方法与ML方法的差距不会明显增大。

计算复杂度方面。在所提方法中，分解信号空间需要进行特征值分解操作，其计算复杂度只有O（）［16］；而 ML方法的计算复杂度随着子载波个数的增加呈指数增加，其计算量是常规器件无法承受的。与ML方法相比，所提方法以较小的性能损失换来低计算复杂度，其优势是明显的。

图4为在参考信号载波间隔Df不同情况下的SINR估计误差，其中信号空间维度Nf＝4.求期望的采样点Nt＝104.从图4看出，仿真结果与理论结果相吻合，所提SINR估计具有良好的鲁棒性。从图中还可以看出：随着参考信号选取密度的增加，SINR估计误差减小；随着参考信号选取密度的减少，信道相关性下降，信号空间矩阵的最小特征值增大，导致SINR估计误差增大。

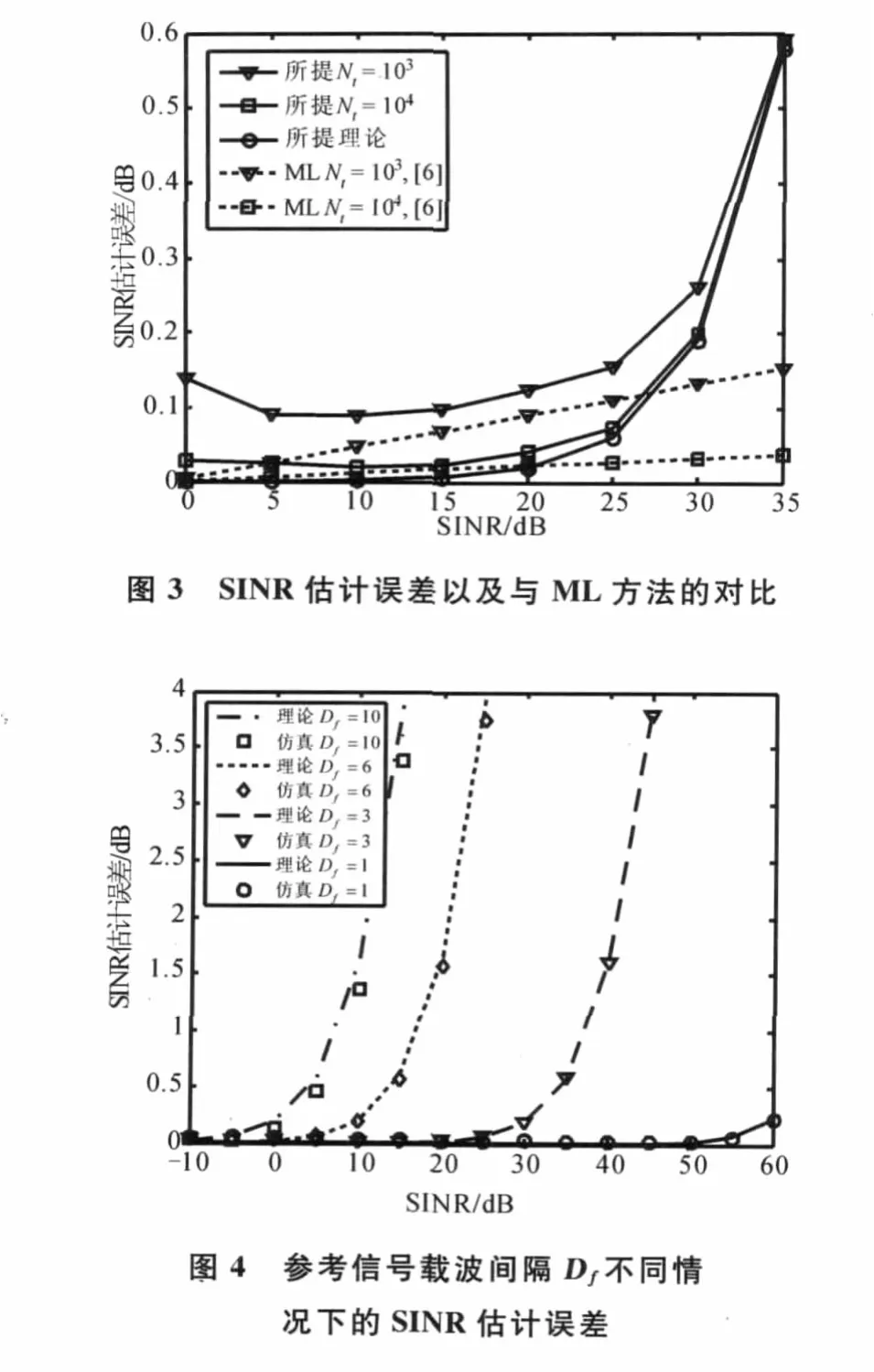
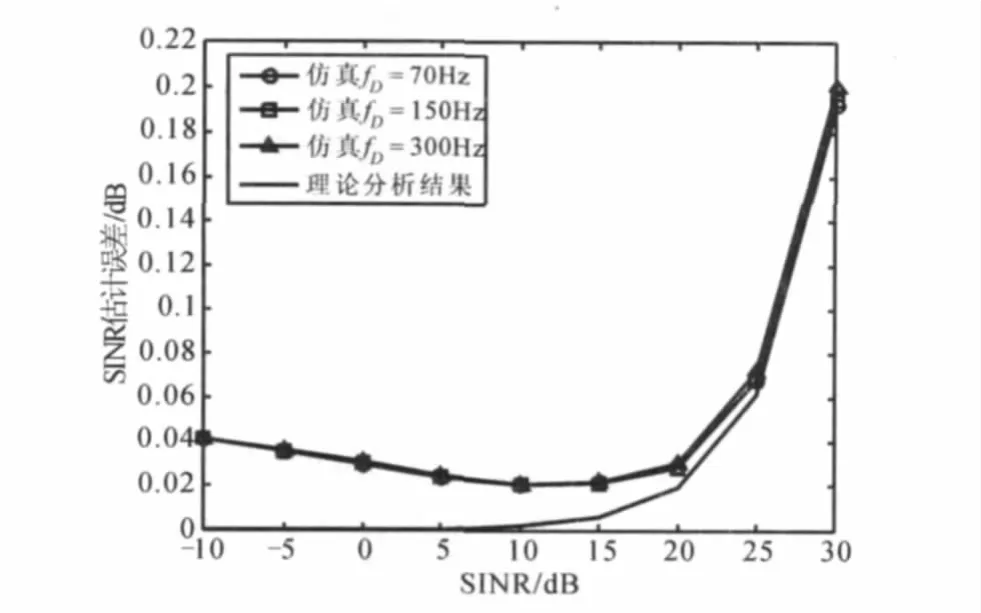
图5 最大多普勒频移不同情况下的SINR估计误差

图5为在最大多普勒频移不同情况下的SINR估计误差，其中信号空间维度Nf＝4，参考信号载波间隔Df＝3，求期望的采样点Nt＝104，当终端的移动速度vh分别为3 0km／h、6 5km／h和1 3 0km／h时，导致最大多普勒频移fD分别为70Hz、150Hz和300Hz.由图5可以看出，在最大多普勒频移不同情况下，估计误差之间的差别不明显，可见所提SINR估计方法对多普勒扩展不敏感。另一方面，SINR估计误差的仿真结果与理论分析结果相吻合，图中最大差别处两者也只相差0.04dB.

5 结 论

在频率选择性衰落信道中，针对MIMO OFDM的链路特征提出一种低复杂度的SINR估计方法：利用子载波之间的相关性特征构造降秩矩阵，基于信号空间分解来估计SINR。理论分析和仿真表明：在SINR小于30dB的典型工作环境中，所提方法只需要利用连续4个参考信号载波，便可实现估计误差小于0.2dB；所提方法利用频率相关性特征，对多普勒扩展不敏感。该方法可用于MIMO OFDM系统开环和闭环复用模式下的SINR测量。

［1］林 静，甘良才.SFBC－OFDM系统在时频双选择信道下的迭代接收算法［J］.电波科学学报，2009，24（1）：167－173.

LIN Jing，GAN Liangcai.Iterative receive algorithm for SFBC－OFDM systems in time－frequency dispersive fading channels［J］.Chinese Journal of Radio Science，2009，24（1）：167－173.（in Chinese）

［2］TURKBOYLARI M，STÜBER G L.An efficient algorithm for estimating the signal－to－interference ratio in TDMA cellular systems［J］.IEEE Transactions on Communications，1998，46（6）：728－731.

［3］RAMAKRISHNA D，MANDAYAM N B，YATES R D.Subspace－based SIR estimation for CDMA cellular systems［J］.IEEE Transactions on Vehicular Technology，2000，49（5）：1732－1742.

［4］XU Huilin，WEI Guo，ZHU Jinkang.A novel SNR estimation algorithm for OFDM ［C］／／IEEE 61st Vehicular Technology Conference，2005：3068－3071.

［5］SOCHELEAU F－X，AÏSSA－EL－BEY A，HOUCKE S.Non data－aided SNR estimation of OFDM signals［J］.IEEE Communications Letters，2008，12（11）：813－815.

［6］CORVAJA R，ARMADA A G.SINR degradation in MIMO－OFDM systems with channel estimation errors and partial phase noise compensation［J］.IEEE Transactions on Communications，2010，58（8）：2199－2203.

［7］SOROOSHYARI S，TAN C W，POOR H V.On maximum－likelihood SINR estimation of MPSK in a multi－user fading channel［J］.IEEE Transactions on Vehicular Technology，2010，59（8）：4175－4181.

［8］贾维敏，刘卫东，姚敏立，等.基于信号子空间的多维参数联合估计［J］.电波科学学报，2007，22（1）：117－121.

JIA Weimin，LIU Weidong，YAO Minli，et al.Multiple parameters joint estimation via single signal subspace［J］.Chinese Journal of Radio Science，2007，22（1）：117－121.（in Chinese）

［9］NEE R V，PRASAD R.OFDM for Wireless Multimedia Communications［M］.Boston：Artech House Publishers，2000：33－39，96－103.

［10］VITHANAGE C，CEPEDA R，COON J，et al.MIMOOFDM pilot placement algorithms for wideband indoor communications［J］.IEEE Transactions on Communications，2011，59（2）：466－475.

［11］王 晗，汪晋宽.MIMO－OFDM系统信道估计中的最优导频设计［J］.电波科学学报，2008，23（3）：501－505.

WANG Han，WANG Jinkuan.Optimal pilot tone design in MIMO－OFDM systems［J］.Chinese Journal of Radio Science，2008，23（3）：501－505.（in Chinese）

［12］COLERI S，ERGEN M，PURI A，et al.A study of channel estimation in OFDM systems［C］／／IEEE 56th Vehicular Technology Conference，2002：894－898.

［13］GOLDSMITH A.Wireless Communications ［M］.Stanford：Stanford University Press，2005：82－89.

［14］张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2004：613－615，484－492.

［15］3rd Generation Partnership Project.User equipment（UE）radio transmission and reception for evolved UTRA［S］.3GPP TS 36.101V10.2.0，2011.

［16］GOLUB G H等著，袁亚湘等译.矩阵计算［M］.北京：科学出版社，2001：456－545.