具有易追踪性的无可信中心门限签名方案*

李映虎,李方伟,卢 霖

(重庆邮电大学 通信与信息工程学院，重庆 400065)

门限签名是现代电子商务中一种重要的数字签名。自门限签名的思想提出以来，出现了各种各样的门限签名方案。然而，如何构造既高效又抗攻击的签名仍然没有一个固定的模式，大多数方案仍然不能抵御各种内部或外部攻击。如参考文献[1]提出了一种具有可追查性的抗合谋攻击门限签名方案，参考文献[2]指出该方案难以抵抗合谋攻击；参考文献[3]提出了一种不可追踪的抗合谋攻击方案，参考文献[4]指出该方案仍存在合谋攻击问题。

为了进一步提高签名的效率，参考文献[5]提出了基于双线性对的短签名。双线性对成了构造签名的重要工具。基于双线性的签名方案具有签字短、安全、高效等特点，它的提出受到了广泛的关注。参考文献[6]引进了PKG的概念，即可信中心，作用是产生用户的私钥，理论上它必须是完全可信的。大多数文献方案的提出也是建立在可信中心的基础之上。然而在有些环境中 (如Ad Hoc网络)，可信中心并不存在。岳胜等人提出了一种无可信中心门限签名方案[7](以下简称YUE的方案)。此方案虽有一定的理论价值，然而该方案仍存在很大的安全漏洞。同时，在实用性方面，当一个方案受到伪造攻击时，良好的可追查性使得签名能够有效地检查成员内部的签名情况。为此，本文提出了一种新的具有可追查性的无可信中心(t,n)门限签名方案。

1 YUE方案的安全性分析

1.1 对YUE方案的伪造攻击

伪造方案与原签名方案相似,区别仅在于在伪造方案中，办事员充当的是伪造攻击者的身份。在门限签名生成阶段，由于每个成员本质上只起到提供一个随机数的作用，办事员的角色与有可信中心方案中的PKG所起的角色没有区别，而办事员是在成员内部随机指定的，因此不可能完全可靠。下面是办事员伪造签名者Pj的部分签名，进而伪造最终的门限签名。这里假设成员Pk是所指定的办事员，具体伪造步骤如下:

(1)成员Pi随机选择xi∈(i≠j)，然后计算Ui=xiP,并把Ui发送给办事员Pk。同时，办事员Pk随机选择∈，并计算。 上述工作完成之后，办事员Pk计算Ui+Uj′和h=riH2(m,U),并 广 播h给{Pi}(i≠j)。

(2)各个成员Pi计算其部分签名并把Vi发 送 给 办 事 员Pk。Pj的 部 分 签 名由Pk计算（其中，Sj已广播）。

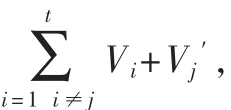
1.2 伪造签名方案的合理性分析

验证者验证最终伪造签名的正确性证明如下：

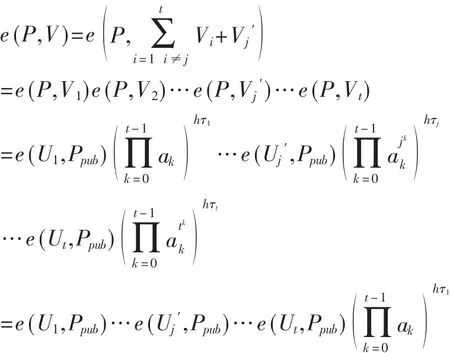
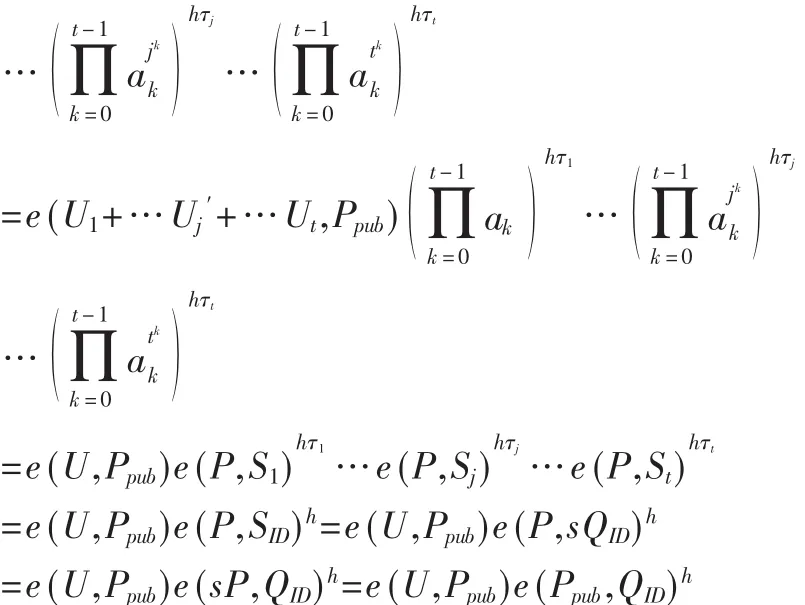
2 新方案的算法描述

2.1 系统初始化过程

设G1为加法群，G2为乘法群，G1、G2的阶均为素数q，P为G1的生成元。定义一个双线性映射e:G1×G2→G2和 2 个单向哈希函数H0:{0,1}*→G1、H1:{0,1}*→。假设系统有n个群成员，设为{P1,P2,…,Pn}，每个群成员都有一个自己的IDi，并公开。

2.2 群密钥的生成

(1)各成员Pi随机选取ki∈,计算QIDi=H0(IDi)，SIDi=kiH0(IDi)，Ki=kiP。 并公布Ki、QIDi。

(2)各Pi随机选取t-1次多项式fi(x)=ai0+ai1x1+ai2x2+…+,计算 λij=fi(IDj)并将其秘密发送给Pj(j≠i)。同时，Pi计算并向其他成员广播 αij=e(aij,P)。当成员Pj获得 λij后，通过进行验证，若不成立，则拒 绝 λij。

2.3 部分签名的生成与验证

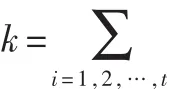
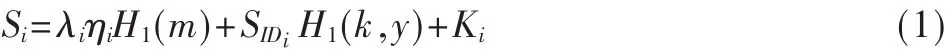
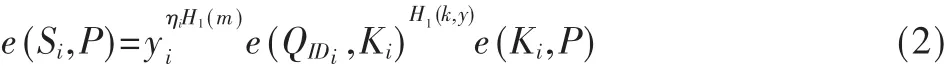
2.4 门限签名的生成和验证

(1)假设签名合成者收到的t份部分签名(Ki,m,Si,IDi)都是合法的，则计算:

当各成员Pi都完成了部分签名分量Si的构造时，随机选取一个成员作为门限签名合成者，并将所有的部分签名发送给它。

作为最终的门限签名,即(m,k,v,S),其中Ki)。

(2)签名接收者根据下式验证(m,k,v,S)的正确性:

3 新方案的分析

3.1 签名的正确性分析

(1)对部分签名的正确性验证即验证,式(2)的正确性:

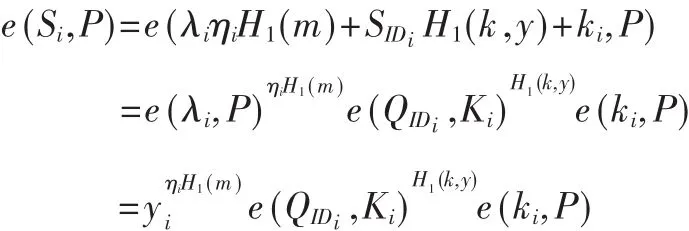
(2)对整体签名的正确性验证,即验证式(4)的正确性:

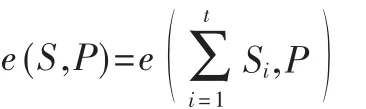
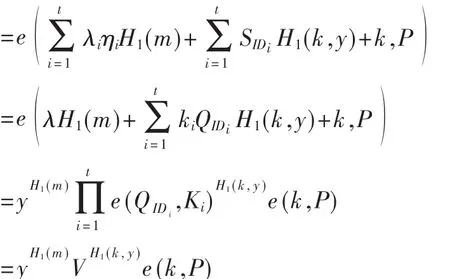
3.2 新方案的安全性

(1)签名不可伪造性

任何第三方不能伪造群体对消息m′进行合法的签名。 由门限签名合成式(3)可知，即使知道了k′、H1(m′)，由于不知道∑SIDi，因此仍不能构成满足式(4)的合法门限签名。另外，任何第三方也不能伪造合法成员Pi而进行部分签名。由于在部分签名生成的过程中，要用到成员Pi的ki、SIDi，而它们是任何第三方都不能获知的，因此无法提交合法的部分签名

(2)方案强壮性

本方案在签名的生成过程中，用到了只有合法签名者自己知道的随机数ki，也就无法求得SIDi。因此，即使恶意攻击者贿赂了某些成员，使其在签名协议中不按照规定执行，最后也无法得到正确的签名。

3.3 性能分析

一个好的门限签名方案，必须要有很好的强壮性及不可伪造性，并且在受到攻击的时候还要有好的可追踪性。同时计算量的多少是方案效率高低的重要指标，很大程度上影响着方案的可行性。本方案与原方案的性质比较如表 1 所示。 令Pl、Mu、Ha、Pa、Ex分别表示群上的乘法和加法运算、哈希函数运算以及配对运算和指数运算。本方案与原方案计算量的比较如表2所示。

表1 本方案与原方案性质比较

表2 签名与验证过程所需的计算量比较

从表1可以看出，原签名方案的强壮性和不可伪造性都低于本方案，同时，本方案有很好的追踪性，而原方案没有。从表2可以看出，在部分签名生成算法中，YUE方案比本文方案多了一次乘法运算，少t次加法运算及2t-1次哈希运算。在部分签名验证算法中，YUE方案比本文方案多用了2t次乘法运算以及2t次指数运算，少使用t次配对运算及2t次哈希运算。在门限签名验证算法中，YUE方案比本文方案多使用一次配对运算，少使用一次指数运算。YUE方案无身份追查，而本文的身份追查只需t次哈希运算。由以上可以看出，本文方案总的运算量为(4t+1)Mu+(3t-1)Pl+2Ex+(3t+2)Pa+5tHa，岳胜等人的方案总的运算量为 (6t+2)Mu+(2t-1)Pl+(2t+1)Ex+(2t+3)Pa+Ha。由此，本方案总运算次数与YUE方案差不多，但却非常有效地防治了各种内部或外部攻击，安全性远远高于YUE方案，而且本方案可以简易地进行身份追踪，实用性更强。

3.4 新方案的易追踪性

当发生纠纷时，群中任何成员都只需查看部分签名中的IDi就可以追查出参加签名的t个成员身份。

4 构造签名的思想

已有大量文献虽然对如何构造签名做出了研究，但至今仍没有一个被广泛认可的构造签名方案或策略。在此，分析几类容易出现安全问题的签名构造[4]。

(1)在门限签名中，签名合成者(DC)负责部分签名的合成，同时负责最终签名的生成，在有可信中心的签名方案中还具有派发密钥的权力。如果签名合成者和伪造者进行合谋，则他们很容易伪造签名。因此，任何门限签名方案都应该考虑对签名合成者加以限制。参考文献[7]提出的门限签名方案将门限签名的密钥发放权、签名合成权集结于办事员，这样的权力分配给签名方案带来了安全隐患。

(2)在构造成员的部分签名或最终签名时，应尽量使所构造签名的前后参数具有相关性，最好通过不同的函数运算（如哈希函数、指数运算）来保证签名参数的前后关联性。这样可以有效地防止各种内部或外部攻击。

(3)参考文献[4]指出为了有效防止中断协议攻击，可以在每次的签名中附加时间戳。同时，适当使用“添加随机数、消息源可识别数字签名”等方法，可以增加合谋伪造攻击的难度。

本文对原有的门限签名进行了安全性分析，指出其在构造最终的签名时前后的参数没有关联，导致最终的方案存在安全隐患。本文提出的新方案构造的签名有效地利用了前后参数之间的联系，不仅解决了原有方案的缺陷,同时很好地抵御了各种外部攻击和内部合谋攻击。

[1]张文芳,何大可,王宏霞，等.具有可追查性的抗合谋攻击门限签名方案[J].西南交通大学报,2007,42(4):461-467.

[2]徐光宝,姜东焕.具有特权者的门限签名方案[J].计算机工程与应用,2011,47(9):83-85.

[3]Gan Yuanju.Verifiable threshold signature against conspiracy attack[J].Journal of Zhejiang University Science,2004,5(1):50-54.

[4]侯整风,赵香,杨曦.抗合谋攻击的门限签名方案[J].计算机工程,2008,34(17):147-148.

[5]BONEH D,LYNN B,SHACHAM H.Short signatures from the weil pairing[C].Boyd C.LNCS 2248:Advances in Cryptology Asiacrypt’ 2001.Berlin:Springer,2001:514-532.

[6]SHAMIR A.Identity-based cryptosystems and signature schemes[C].LNCS 196:Advances in Cryptology-CRYPTO 1984.Berlin:Springer,1984:47-53.

[7]岳胜,辛小龙.一种无可信中心门限签名方案[J].计算机工程与应用,2011,47(3):87-89.

[8]达青峰.一种标准模型下基于身份的高效门限签名方案[J].计算机工程与应用,2010,46(21):76-79.

[9]吕鑫,王志坚,许峰.基于双线性对的新型门限签名方案[J].计 算 机 科 学,2011,38(4):111-114.

[10]Liu Danni,Wang Xingwei,Guo Lei,et al.A dynamic threshold signature scheme with provable security[C].2010 2nd International Conference on Future Computer and Communication,2010:322-324.

[11]杨长海.基于身份的门限多代理多盲签名方案[J].计算机工程与应用,2010,46(18):121-124.

[12]王斌,李建华.无可信中心的门限签名方案[J].计算机学报,2003,26(11):1581-1584.

[13]杨胜良.Lagrange插值公式的几种构造性证明[J].大学数学,2004,20(3):47-50.