基于S变换的雷达脉内调制特征提取方法*

张彦龙，张登福，王世强，陈 雕

（空军工程大学 工程学院航空电子工程系，陕西 西安710038）

雷达辐射源信号分选是现代高技术战争和将来的信息化战争中至关重要的环节，也是当前电子情报侦察系统(ELINT)和电子支援系统(ESM)中的技术瓶颈[1]。依赖于常规参数进行雷达信号分选是现代雷达对抗中的经典方法。然而，对于复杂体制雷达共存以及高密度信号环境，经典方法已很难获得令人满意的分选效果。近年来，随着DSP与VLSI技术的成熟，数字中频接收机已能够较全面地获取雷达信号的脉内信息[2]。因此，当前研究方向趋向于通过对雷达信号脉内数据进行分析，研究脉内调制特征，以便快速、准确地分选信号。

利用信号的时间频率联合分布来刻画雷达辐射源信号的调制信息，能够有效提取脉内有意调制特征。参考文献[3-5]分别利用短时傅里叶变换（STFT）、Wigner-Ville分布(WVD)和小波变换等时频分析方法提取脉内调制信息。Stockwell等[6]提出的S变换是近年来人们研究非平稳信号时频分布的一个重要工具,是一种具有多分辨率特性、时频分辨率与频率相关、介于短时傅里叶变换和小波变换之间的时频分析方法。S变换吸收并发展了短时傅里叶变换和连续小波变换，在时间域和频率域中能较好地表现信号的局部特征，且其正反变换可通过FFT实现[7]。因而相对于Wigner-Ville分布，S变换更有利于信号的快速处理。

鉴于上述原因，本文将S变换引入到雷达信号的时频分析领域，致力于利用S变换提取雷达辐射源脉内调制特征并进行分类实验。文中对6种典型雷达辐射源调制信号进行了分类仿真实验，验证了本文方法的有效性。

1 S变换理论

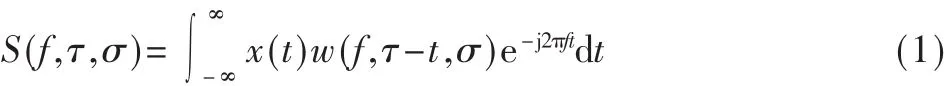
式中 S(τ,f)是信号 x(t)的 S变换，τ和 t是时间变量，f是频率变量。σ是调节因子，可以加快或减慢时窗宽度随频率f呈反比变换的速度。

本文对雷达辐射源脉内信号进行S变换分析，σ值取为2，得到了较好的效果。图1给出了典型的常规雷

一维信号x(t)的连续S变换定义为[6]:达信号(CW)、线性调频雷达信号(LFM)、二相编码雷达信号(BPSK)、四相编码雷达信号(QPSK)、非线性调频雷达信号(NLFM)和脉内频率编码雷达信号(FSK)的6种脉内调制信号S变换结果。可以看出S变换时频图反映出信号的不同调制信息。

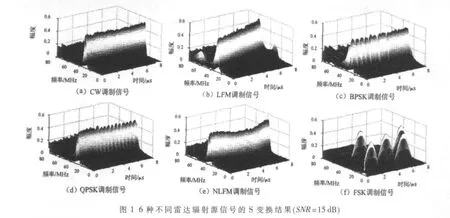
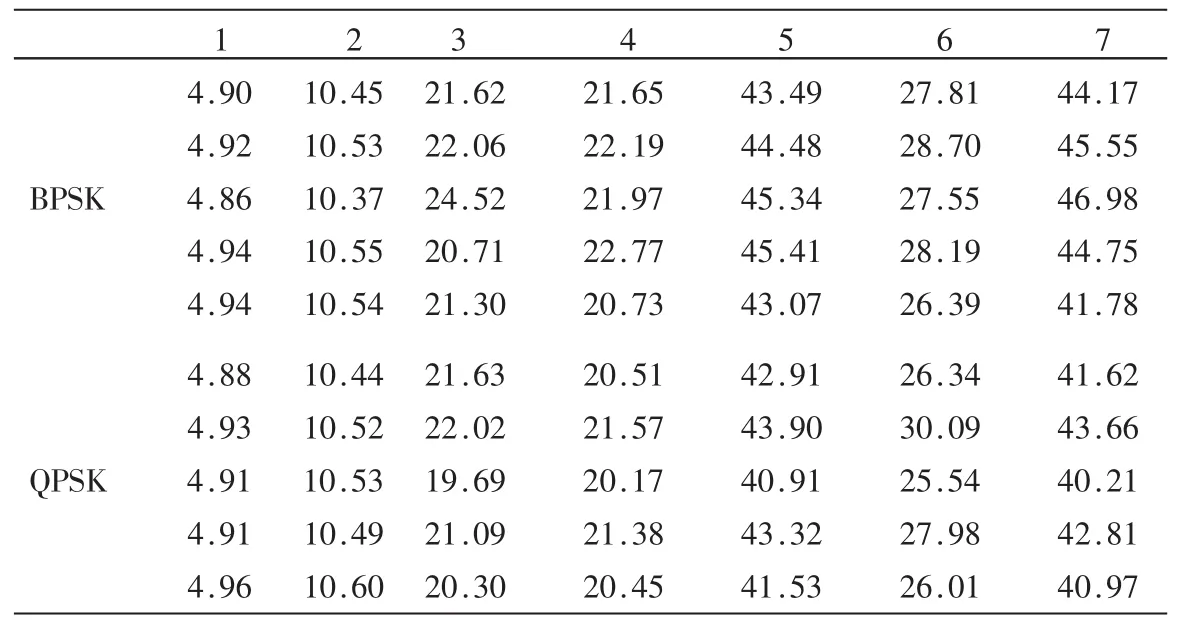
表1 随机样本不变矩特征（SNR=5 dB）

2 雷达辐射源信号脉内调制特征提取

2.1 基于时频图像不变矩特征提取方法

图像的不变矩特征是一种在图像分类识别领域广泛应用的图像统计特征参数[8]。矩在统计学中用于表征随机量的分布,将信号的S变换结果转化为 M×N的灰度图像 f(x,y),其(p,q)阶中心矩定义为：

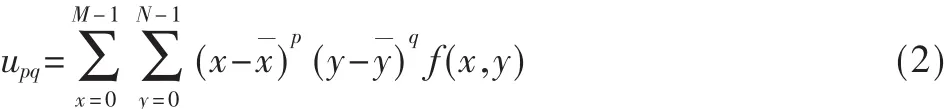
不变矩描述了一幅灰度图像中所有像素点的整体分布情况和基本几何特征。结合图1中信号的S变换结果，时频图像的几何特征主要表现为不同的频率变化规律。相对于其他调制信号，BPSK和QPSK的信号载频一样,仅存在相位上的差异,反映在图像几何特征上的差异性较小。表1给出了BPSK和QPSK信号中5个随机样本的7个不变矩特征。结果表明，BPSK和QPSK信号的同一不变矩特征数值相近,很难分辩出这两种信号，因此需要提取新的特征。

2.2 联合特征提取方法

S变换的幅值表示辐射源信号分量能量的大小，幅值越大，相应时间点和频率点的信号分量能量越大。因此可以用S变换的峰值变化规律最大程度地表征信号真实的频率变化信息。由图1可以看出相位和频率的突变会引起S变换峰值剧烈变化。图2给出了BPSK和QPSK调制信号的S变换峰值包络对比图。对于BPSK和QPSK信号，因相位调制规律不同，其S变换峰值的变化规律和大小也不相同。

如果将峰值包络波形作为信号脉内调制特征，则特征维数过高，同时存在许多无效和冗余信息，势必增加后续分选处理的复杂性，降低信号处理的实时性。考虑到信息熵是从平均意义上表征信源总体信息测度的一个量，同时又是信源输出信息的不确定性和事件发生的随机性的量度，因此考虑引入熵的概念，两次提取包络的均值和波形熵来表征峰值包络的变换和分布情况。本文将不变矩特征和峰值包络熵特征相结合，兼顾两者的优势形成联合特征。

设包络特征序列为 W=[w1,w2,…,wN]，则波形熵的定义为：

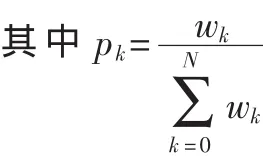
3 仿真实验

为了验证本文方法对复杂体制辐射源信号特征提取的有效性,选取6种典型雷达辐射源信号：CW、LFM、NLFM、BPSK、QPSK和FSK。辐射源信号载频为 30 MHz，采样频率为 200 MHz,脉冲宽度均为8 μs，LFM调频宽度为15 MHz；NLFM采用正弦调频信号，调频宽度为10 MHz；BPSK采用13位巴克码；QPSK采用16位法兰克四相码；FSK采用5频率编码信号。

3.1 不变矩特征分类实验

考虑到支持向量机在小样本分类上的优势，本文选择支持向量机作为分类器。在实验中，对于每种辐射源信号在 0～20 dB之间的信噪比(SNR)范围内,每隔 5 dB产生100个辐射源信号。每一信噪比下总共有600个辐射源信号样本。采用支持向量机对其进行分类实验，分类正确率采用100次实验的统计平均值，随机选择50%的样本作为训练样本。表2给出了不同信噪比下6类调制信号的分类实验结果。

由表2可知，基于图像不变矩特征的分类正确率随信噪比的增加而上升，但对 CW、BPSK和QPSK信号分类正确率明显较低。SNR=10 dB时,BPSK信号分类正确率只有 69.6%,显然不满足要求，同时,实验也验证了本文对不变矩特征分析的正确性。

3.2 基于联合特征的分类实验

不变矩特征的低阶距特征反映了图像的整体特征，不包含太多的细节信息，而高阶矩(三阶)对噪声特别敏感[10]。考虑到尽可能地降低特征维数并结合实验分析，选择不变矩的一阶矩、峰值包络的均值和波形熵组成三维特征向量 P′=[φ1,μ,Ew]作为雷达辐射源信号的脉内特征向量，然后进行归一处理。图3给出了当信噪比（高斯白噪声）分别为 20 dB、15 dB、10 dB和 5 dB时，某次,试验中6种典型调制信号的三维特征分布图。其不同信噪比环境下各类信号分类实验结果如表3所示。

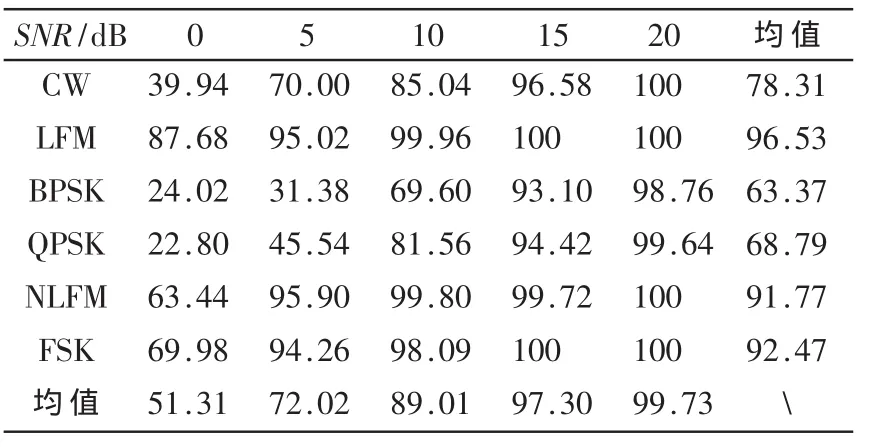
表2 不同信噪比下分类正确率/%

实验结果表明，在一定信噪比下，提取的特征具有较好的聚集性和可分性。同时联合特征弥补了图像不变矩特征对于CW、BPSK和QPSK信号分类正确率较低的不足,从而验证了该算法的有效性和可行性。另外，由于在低信噪比下(0dB)BPSK和QPSK信号的相位信息受噪声干扰较大，S变换峰值包络很难完整地反映相位的变化信息，从而降低了提取特征的分类能力。

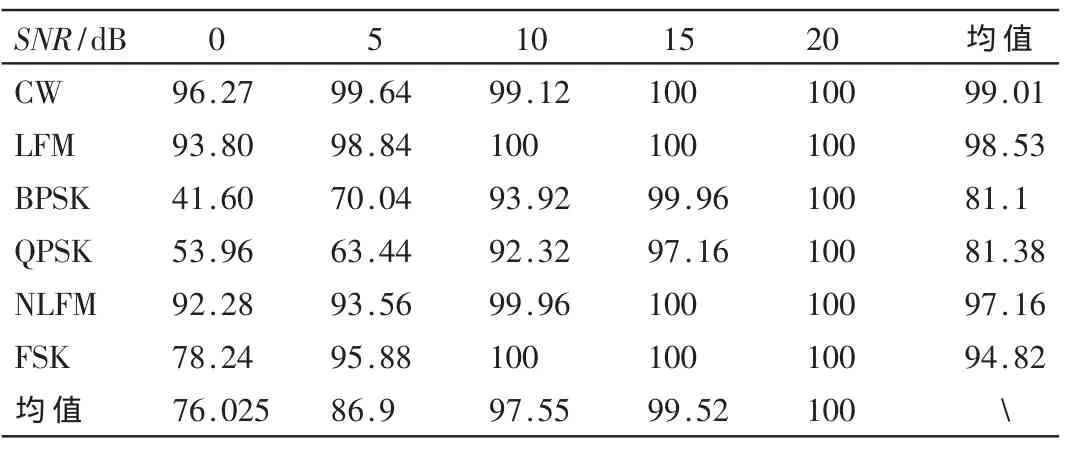
表3 不同信噪比下分类正确率/%

实验同时比较了采用STFT、WVD和ST的分类实验结果，信噪比分别为 0 dB、5 dB、10 dB、15 dB和 20 dB时的实验结果如图4所示。

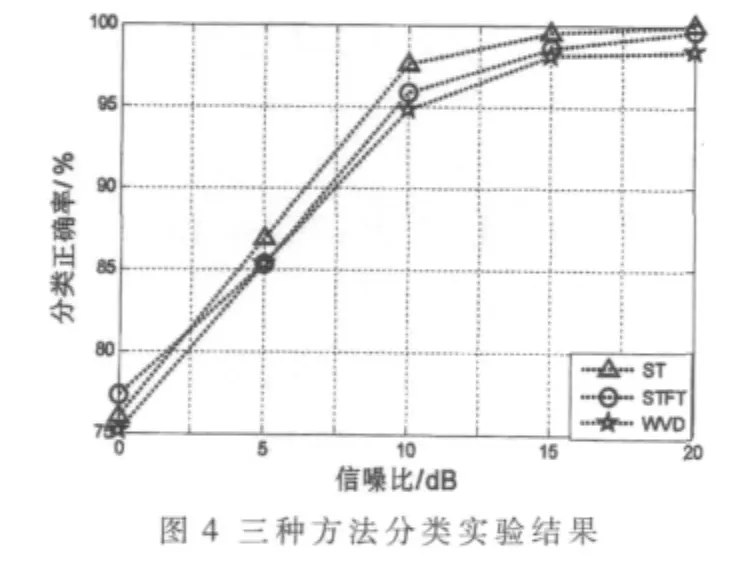
图4中的结果表明,基于ST的联合特征提取方法的分类实验效果要优于基于STFT和WVD的实验效果，这是由于WVD得到的时频图本身受到交叉项的噪声、干扰，导致不变矩特征分类能力下降。相对于STFT变换，S变换具有更好的时频分辨率，及更好的分类性能。

本文通过对S变换时频图像不变矩特征进行分析，提出了基于不变矩特征和S变换峰值包络熵特征的联合特征提取方法。应用支持向量机对6种典型调制信号进行了分类仿真实验。结果表明该方法提取的特征在一定信噪比下具有较好的聚集性和可分性，对不同调制信号均取得了较好的正确分类率，验证了该算法的有效性。但在低信噪比情形下，分类效果仍需要进一步提高。

[1]WILEY R G.ELINT:The interception and analysis of radar signals(Second Edition)[M].Boston,MA:Artech House,2006.

[2]陈韬伟.基于脉内特征的雷达辐射源信号分选技术研究[D].成都：西南交通大学,2010.

[3]刘东霞.脉内调制信号的分析与自动识别[D].西安电子科技大学,2003.

[4]余志斌,金炜东,陈春霞.基于小波脊频级联特征的雷达辐射源信号识别[J].西南交通大学学报,2010(2)：290-295.

[5]Guo Qiang,Li Yajun,Wang Changhong.Novel detection method for multi-component LFM signals[C].2010 First International Conference on Pervasive Computing,Signal Processing and Applications,2010.

[6]STOCKWELL R G,MANSINHAL L,LOWE R P.Localization of the complex spectrum:the S-transform[J].IEEE Transactions on Signal Processing,1996,44(4):998-1001.

[7]PINNEGAR C R.Time-frequency and time-time filtering with the S-transform and TT-transform[J].Digital Signal Processing,2005(15):604-620.

[8]TEH C H.On image analysis by the methods of moments[J].IEEE T-PAMI,1988,10(4):496-513.

[9]HU M K.Visual pattern recognition by moment invariants[J].IRE Transactions on Information Theory,1962,8(2):179-87.

[10]徐旦华,辜嘉,李松毅,等.Zernike矩的快速算法[J].东南大学学报,2002,32(2):189-192.