斜拉索基频识别技术

(华南理工大学土木与交通学院，广东广州 510640)

0 引言

近十年来，斜拉桥在国内已成为主要桥型之一，在施工及后期运营状态中有一项重要的内容，就是索力的测量，索力测量的方法有:油压表法、压力环测量法、频率法等。前两种是直接测量法，后一种是间接法。这些方法均在实桥中有应用［1］，其中精度较高的有压力环测量法以及频率法。压力环测定:直接在斜拉索锚头下安装压力环，一侧靠锚具，另一侧靠锚垫板，这种方法最直接，精度高，但成本高，对锚垫板平整度要求高，仪器重不便于操作。频率法:通过在斜拉索上安装加速度传感器，获取斜拉索在自然振动激励下的时程曲线，经低通滤波、放大信号和快速傅里叶变换，得到自功率频谱图来确定斜拉索的自振频率，然后由相应公式计算索力。频率法测索力的优点:安装测量简单，设备可多次使用，根据现有仪器水平及分析技术，测定拉索频率的精度可达到 0.002 Hz，即索力值精度可达 0.6 t～1.2 t，足以满足工程要求。频率法适用于没有预先安装传感器情况的现役斜拉桥的索力测量，精度高，测试速度快［2］。频率法测索力是目前确定斜拉桥索力最广泛使用的一种方法［3］，作为一种由频率间接换算索力的方法，振动法测索力的关键在于如何由实测数据得到正确的拉索频率值以及准确的索力、频率对应关系。

1 工程概况

崖门大桥是广东省西部沿海高速公路建设项目的重点工程之一，大桥为双塔单索JP2面预应力混凝土斜拉桥，采用塔梁固结柔性墩体系［4］。每侧边跨设置一个辅墩，跨径组合为(50+115+338+115+50)m，全桥总长668 m。主梁是单箱五室预应力混凝土梁，梁高3.48 m，桥面全宽26.8 m，设双向四车道。主墩为双壁柔性墩，横向宽12 m，双壁之间中心距6 m，墩高47.6 m。桥面以上塔柱高73.5 m，塔柱断面为单箱混凝土断面。全桥共有斜拉索200根，主梁标准索距6 m，桥型布置图见图1。

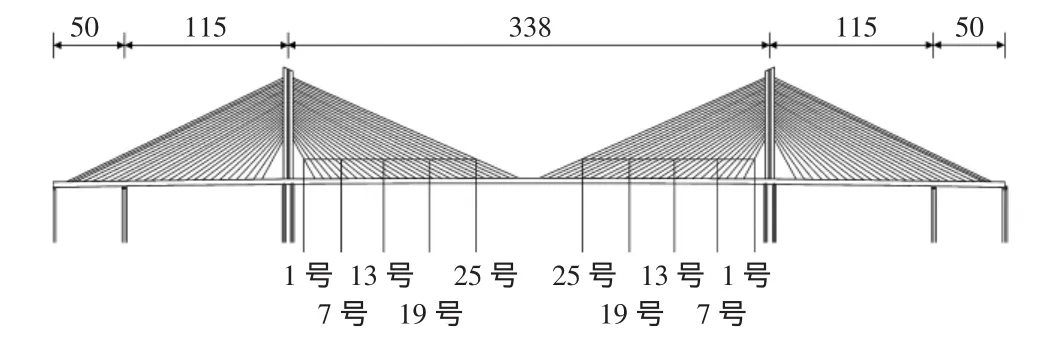
图1 崖门桥桥跨布置图（单位：m）

本文采用压电加速度传感器LC0406进行斜拉索振动测试，生产厂家为朗斯测试技术(秦皇岛北戴河)有限公司，测试系统框图见图2。

用上述测试系统分别于2007年，2008年，2010年，2012年对该桥索力进行通测，2007年测试结果作为长期监控初始值;传感器置于桥面以上2 m左右，测试值为加速度时程曲线，方向垂直于索线;测试参数［5-8］:采样频率80 Hz，低通滤波50 Hz，采样时间204.8 s，FFT 点数 1024，重叠率 3/4。

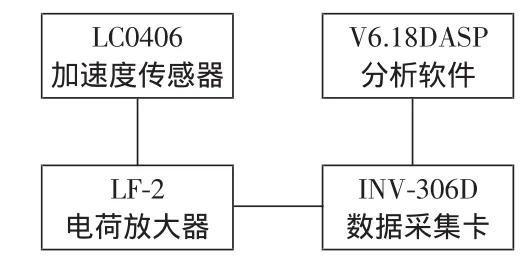
图2 崖门大桥索力测试系统

2 斜拉索基频识别

根据文献［9］［10］，当拉索索力一定的时候，理想的情况其经过FFT变换得到的自功率谱上的峰值应该是等间距的，且峰值间距应该等于斜拉索振动的基频。这是因为理想的斜拉索索力与其自振频率关系公式知，当索力一定时，高阶频率是基频的整数倍。在一般的测试环境下，由于各种干扰，在低频部分往往出现不了频谱峰值，以前在现场测试时的做法通常是:不考虑自振频率的阶数，仅计算功率谱上比较明显的相邻峰值间距，以此作为拉索的基频值。但实际上，由于斜拉索存在一定的抗弯刚度等原因，导致实测拉索频率阶数越高，频差越大。如图3所示，为一根短索的自功率谱图，根据峰值间间距可判断第一峰值即为其基频值。因为短索由于其基频较大(大于2 Hz)，与桥面震动不容易混叠，故能从频谱图上清晰地识别出来。即该索基频为2.03。

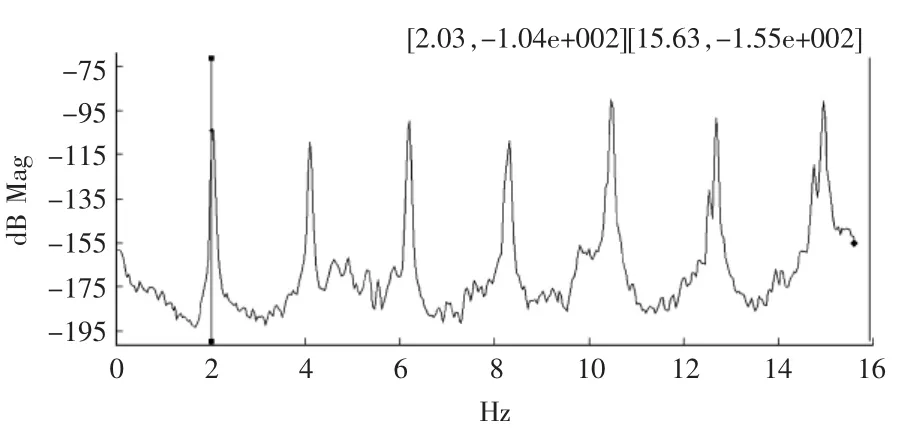
图3 自功率谱密度（一）

另外，将频谱图峰值相减，结果见表1，可明显看出峰值间距越往高阶越大，识别出的基频误差越大，从而影响了索力测量的精度(基频变化0.01，计算出的索力值变化4 t～6 t)。

由于测试条件限制，索力测试时传感器只能放在索离地面2 m处，环境振动功率谱代表前几阶频率的峰值很容易混淆，所以难以从频谱图上直接看出基频值，甚至无法确定功率谱上的峰值对应的固有频率的阶数。这是由于较长斜拉桥的拉索的基频相当低，其功率谱的低频部分有时涉及与桥面板或桥塔的基频的耦合。从频谱图上难以观察出其基频的位置，只能识别出其高阶频率，如图4所示，为一根长索自功率谱密度，其峰值间距约为1.6，故知第一峰值为其二阶频率，其基频约为3.13/2=1.565(见表2)。

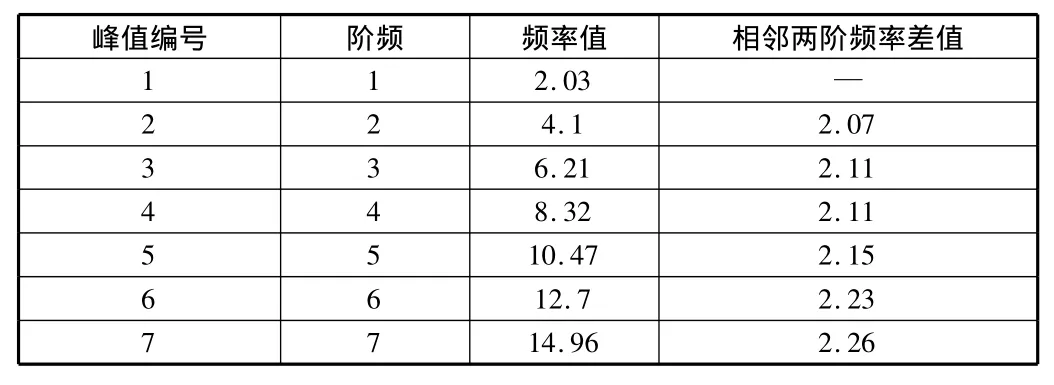
表1 短索自功率谱密度峰值

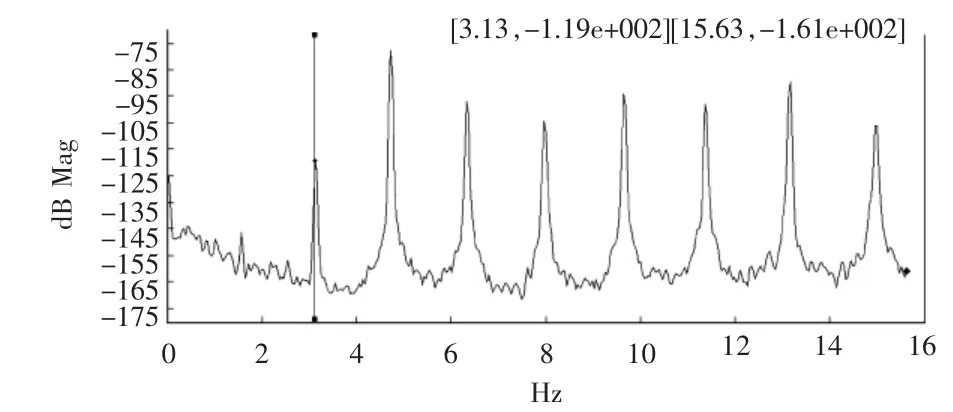
图4 自功率谱密度（二）

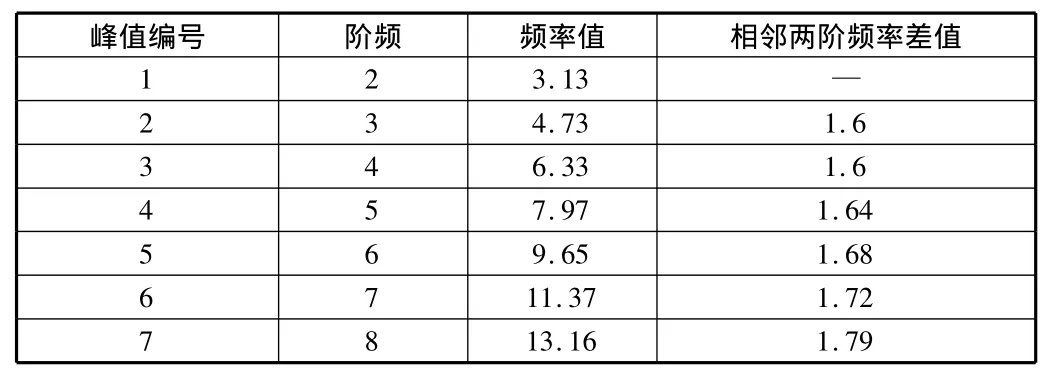
表2 长索自功率谱密度峰值

较长斜拉索的前几阶频率通常不能被识别，但直接利用高阶频率差值，或用高阶频率除以其阶数求基频就会造成基频识别值偏大(用7阶频率计算出的基频比实际基频大0.23)，导致计算出索力值偏大，故本文采用二次拟合的方法计算其前几阶的频率。

图5a)是东塔上游25号索的各阶频率拟合结果，从频谱图识别第4阶～第20阶频率，以二次曲线进行拟合。实测的和拟合的各阶频率差值见图5b)。可见，实测各阶频率的差值最小为0.703 Hz，最大为0.79 Hz，且各阶频率差值的分布无序;而拟合的各阶频率的差值变化是平缓的，从0.731 Hz～0.767 Hz，与文献［11］的结论较为吻合。

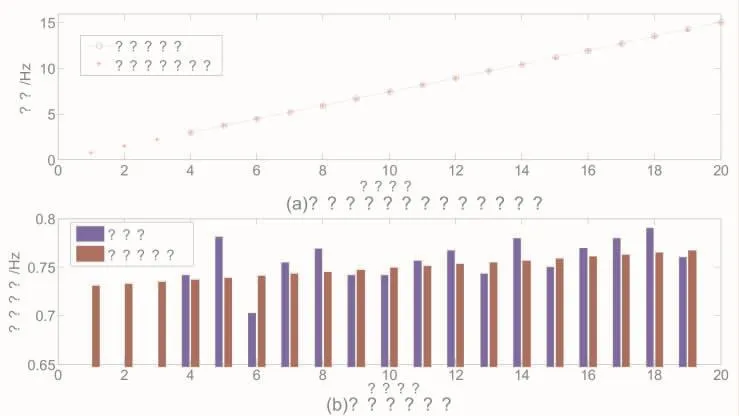
3 识别结果

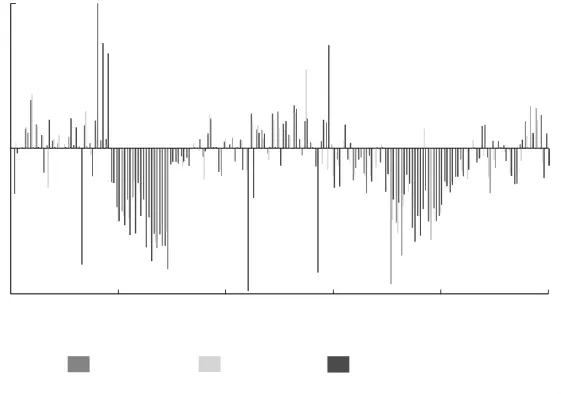
运用上述基频识别方法及文献［1］中所推导的索力计算公式，对崖门大桥三次长期监控的索力测试结果(2008年，2010年，2012年，仅给出上水测量值)列于图6，图7。从图6，图7中可以看出:1)桥梁全桥的索力分布比较均匀、对称;2)三次的索力测试结果的变化率均不大，在5%之内;3)个别斜拉索的变化率较大，可能是由于测试过程中有重车经过，造成一定的误差。

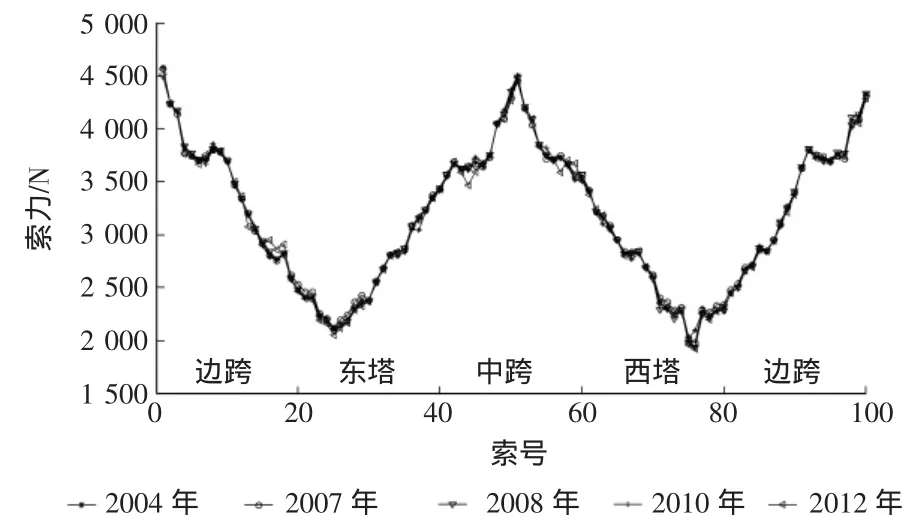
图6 上水斜拉索索力对比图

4 结语

通过频率识别和索力识别结果，可知主梁和索在0 Hz～3 Hz范围内有共振现象;二次拟合法比频率间距法能更准确地识别出较长拉索的低阶频率;在垂度不大的斜拉索索力测量中，可用抛物线代替悬链线，具有足够的精度。崖门大桥的中跨斜拉索索力分布比较对称均匀，测量结果可靠;总体来看，由于混凝土收缩徐变作用，主塔周围的短索索力趋向于减小，而长索索力趋向于变大。个别索索力变化较大，可能是受到测试环境的影响，或是出现松弛，应该多次测试予以确认，保证桥梁结构安全。

［1］王卫锋.PC斜拉桥的施工监测［D］.广州:华南理工大学博士论文，2000.

［2］郭良友，林一宁，李文波，等.武汉长江二桥的索力、温度和应力测量［J］.桥梁建设，1995(3):44-53.

［3］苏 成，徐郁峰，韩大建.频率法测量索力中的参数分析与索抗弯刚度的识别［J］.公路交通科技，2005，22(5):75-78.

［4］华南理工大学城市建设研究中心.广东省西部沿海高速公路崖门大桥施工监控工作总结［R］.2002.

［5］王卫锋，徐郁峰，韩大建，等.崖门大桥施工中的索力测试技术［J］.桥梁建设，2003(1):23-26.

［6］戴诗亮.随机振动实验技术［M］.北京:清华大学出版社，1984.

［7］吴天毅.测试技术与测试信号处理［M］.北京:清华大学出版社，1991.

［8］张阿舟.实用振动工程(3)——振动测量与试验［M］.北京:航空工业出版社，1997.

［9］韩 锋，申彦鹏.基于傅里叶变换的斜拉索振动频率识别研究［J］.西部交通科技，2010(7):91-92.

［10］陈 刚，任伟新.基于环境振动的斜拉桥拉索基频识别［J］.地震工程与工程振动，2003(3):23-24.

［11］侯立群，欧进萍，赵雪峰，等.哈尔滨四方台斜拉桥模态参数和索力识别［J］.振动与冲击，2009，28(5):106-110.