欧氏空间的等积变换的性质
王朝霞,张 庆
(唐山师范学院 数学与信息科学系,河北 唐山 063000)
数学研究
欧氏空间的等积变换的性质
王朝霞,张 庆
(唐山师范学院 数学与信息科学系,河北 唐山 063000)
首先给出了欧氏空间的等积变换的定义。其次给出4个引理并利用这些引理给出了有限维欧氏空间的两个线性变换为等积变换的充要条件,其中一个充要条件反应了两个等积变换在规范正交基下的矩阵关系,另一个充要条件反应了两个等积变换之间的关系。最后给出了无限维欧氏空间为等积变换的一个充要条件及等积变换的一个性质。
欧氏空间;线性变换;等积变换;规范正交基
1 引言
在欧氏空间V中,若,σ τ 为V的两个正交变换,则对任意的ξ, η∈V,都有
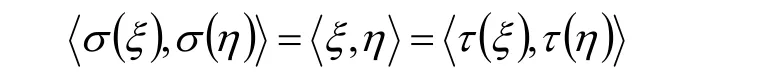
反之,如果对任意的ξ, η∈V,都有
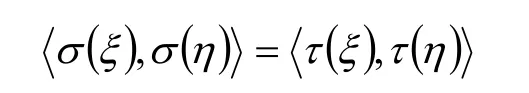
那么,σ τ 未必是为V的两个正交变换。本文要研究保持内积不变的同一欧氏空间的两个线性变换的关系。
2 预备知识
定义 在欧氏空间V中,,σ τ 为V的两个线性变换,若对任意的ξ, η∈V都有
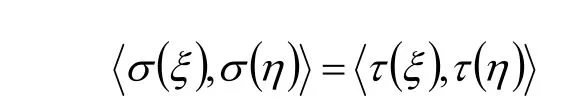
则称,σ τ 为V的两个等积变换。
引理1[1]若V是欧氏空间,V的向量组
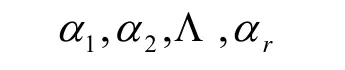
线性无关的充要条件是及
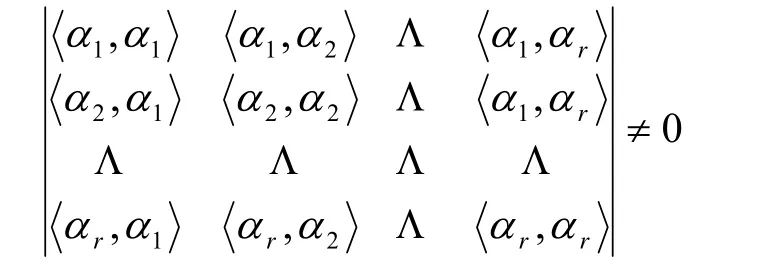

引理2 若V是欧氏空间,V的两个向量组为由X, Y的任意性知ATA=BTB=0,即ATA=BTB。


由引理及定理1可得定理2。
定理2 若σ,τ为n维欧氏空间V的两个线性变换,则σ,τ为V等积变换的充要条件是存在正交变换φ,使得φσ=τ。
证明 充分性。若存在正交变换φ,使得σ=φτ,则对任意的ξ,η∈V,都有
σ( ξ),σ( η)=φ( τ( ξ)), φ( τ( η))=τ( ξ),τ( η)
因此σ,τ为V的两个等积变换。
必要性。若σ,τ为V的两个等积变换,设
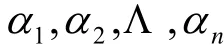
为欧氏空间V的一个规范正交基,σ,τ关于
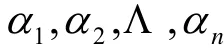
的矩阵分别为A,B,由定理1,ATA=BTB,而ATA的位于第i行第j列的元素为
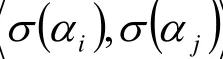
而BTB的位于第i行第j列的元素为
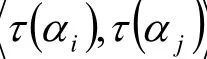
从而
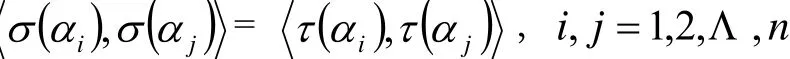
由引理4,存在V的正交变换φ使得

即
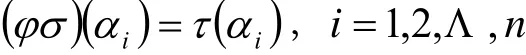
又α1,α2,Λ,αn为欧氏空间V的一个规范正交基,于是φσ=τ。
推论1 设矩阵A,B为n阶实矩阵,则ATA=BTB的充要条件是存在n阶正交矩阵U,使得B=UA。
证明:若σ, τ为n维欧氏空间V的两个线性变换,并且σ, τ关于V的规范正交基α1,α2,Λ,αn的矩阵分别为A,B。由定理1知,ATA=BTB的充要条件σ,τ为V的等积变换,由定理2知σ, τ为V的等积变换的充要条件是存在正交变换φ,使得φσ=τ,设并且正交变换φ关于V的规范正交基α1,α2,Λ,αn的正交矩阵为U,则B=UA。
2.2 无限维欧氏空间的两个线性变换为等积变换的性质
当欧氏空间V不是有限维欧氏空间时,在讨论等积变换时,不能利用规范正交基及矩阵这样的工具,在某些条件下有以下定理。
定理3 若σ, τ为欧氏空间V的两个线性变换,且σ或τ为可逆变换,则σ, τ为V等积变换的充要条件是存在正交变换φ,使得φσ=τ。
证明 充分性的证明与定理2相同。
必要性:若σ, τ为V的两个等积变换,不妨设σ为可逆变换。对任意的ξ,η∈V,设

则α,β∈V。由于σ, τ为V的两个等积变换,则
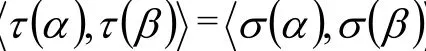
即
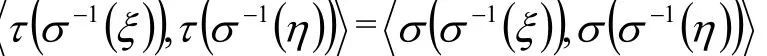
所以
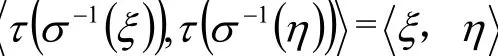
所以,τσ-1为正交变换,令φ=τσ-1,则τ=φσ,其中φ为正交变换。
定理4 若σ,τ为欧氏空间V的两个等积变换,则σ(V )与τ(V )同构。
证明 对任意ξ∈V,令φ: σ( ξ)→τ( ξ),则φ是σ(V)到τ(V)的映射,且为满射。对任意ξ, η∈V,若
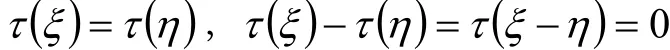
由于σ, τ为V的两个等积变换,则
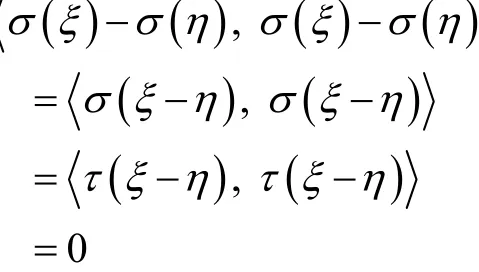
所以,σ(ξ)=σ(η),即φ是σ(V )到τ(V)的单射。对任意的ξ, η∈V及任意实数k, l,
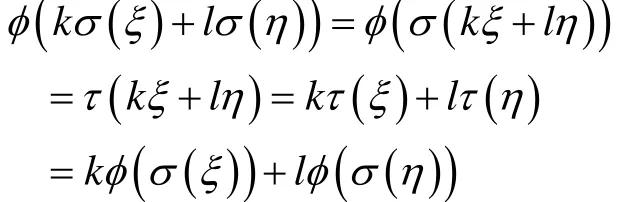
对任意的ξ, η∈V,
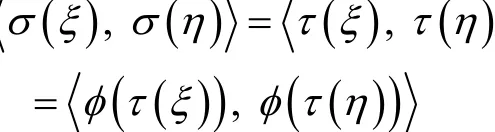
因此,φ是σ(V)到τ(V)的同构映射,亦即σ(V)与τ(V)同构。
[1]王品超.高等代数新方法[M].济南:山东教育出版社, 1989:462-463.
[2]张禾瑞,郝鈵新.高等代数(第5版)[M].北京:高等教育出版社,2007:302.
[3]白述伟.高等代数选讲[M].哈尔滨:黑龙江教育出版社, 1996:312.
(责任编辑、校对:赵光峰)
Properties of the Equi-Inner Product Transformation of Euclidean Space
WANG Zhao-xia, ZHANG Qing
(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)
This Paper introduces the definition of the equi-inner transformation of Euclidean space. Then gives four lemmas and two necessary and sufficient conditions of what the linear transformation is the equi-inner transformation. One of the necessary and sufficient conditions hint the matrix relations between the two equi-inner transformation matrices under standard orthogonal basis, the other one hint the relationship between two equi-inner transformations. Finally, the necessary and sufficient condition and a property are derived for infinite dimension Euclidean space is an equi-inner transformation.
euclidean space; linear transformation; equi-inner product transformation; standard orthogonal basis
O151
A
1009-9115(2012)05-0030-04
2012-07-20
王朝霞(1963-),女,河北唐山人,教授,研究方向为代数。
——课堂的民主集中制

