基于属性加权的不完全数模糊c均值聚类算法

李 丹， 顾 宏， 张 立 勇

（大连理工大学 控制科学与工程学院，辽宁 大连 116024）

0 引 言

聚类是数据挖掘、模式识别等领域的重要研究内容之一，在识别数据内在结构方面具有重要作用.模糊c均值（fuzzyc－means，FCM）算法[1]是一种基于目标函数的有效的聚类算法，该算法能够将p维完整的目标数据集X＝ ｛x1，x2，…，xn｝Rp划分为若干模糊子类.然而，在模式分类应用中，由于数据采集失败及随机噪声等原因，很多数据集是不完全的，即数据集包含缺失部分（非全部）属性值的样本，而FCM算法不能直接应用于不完全数据集的聚类分析.

为了消除缺失属性对聚类分析的影响，有关文献提出了各种不完全数据集的模糊聚类算法[2－8].Miyamoto等[2]提 出 了 几 种 在 模 糊c均 值算法中处理不完全数据的方法，其中一种简单方法是以相应属性的加权平均值估算缺失属性值，另一种方法则忽略数据集中的缺失属性并通过完备属性进行距离测算，这两种方法即后来解决不完全数据聚类问题的常用策略：估算（imputation）法及舍弃（discarding/ignoring）法.之后，Hathaway等[3]提出了基于FCM进行不完全数据聚类的几种具体方法，其中 WDS（whole data strategy）是一种最简单的方法，该方法舍弃样本集中所有包含缺失属性的样本，利用剩余完备样本得到聚类中心及完备样本的类属，不完全样本的类属则通过其与各聚类中心的局部距离[9]确定，但这种对数据集的约简将造成信息的大量丢失；另一种方法为PDS（partial distance strategy），即忽略不完全样本的缺失属性，FCM算法中的距离仍采用Dixon提出的局部距离[9]计算；文献[3]还提出了两种依据数据集信息对不完全样本的缺失属性进行估算的方法，其中 OCS（optimal completion strategy）方法将缺失属性的估算看作优化问题，并在聚类迭代过程中逐步寻求更优的估计值，而NPS（nearest prototype strategy）方法则在每次聚类迭代中将缺失属性设置为距离最近的聚类中心的相应属性值.此外，考虑到样本集中属性的缺失原因，Timm等提出了一种基于Gath－Geva算法的不完全数聚类方法[4]；对于不完全关系数据集，Hathaway等根据三角不等式近似规则提出了一种基于FCM的聚类方法[5]；Honda等则通过局部主成分分析法将不完全数据集划分到若干线性模糊子类中[6]；Lim等提出通过神经网络训练缺失属性以解决不完全数聚类问题[7].鉴于不完全数据中缺失属性的不确定性，作者在前期工作中提出了缺失属性的最近邻区间描述[8]，通过将不完全数据集转化为区间型数据集求解不完全数据集的聚类问题.

上述算法均隐含假定待分析样本的各维属性对聚类的贡献均匀，在实际应用中有一定的局限性.目前，针对完全数据集的属性加权聚类研究十分活跃，研究者已提出了多种属性加权模糊聚类算 法[10－13]，通 过 极 小 化 属 性 评 价 函 数[10]、利 用ReliefF算法[14]进行属性赋权[11]、聚类与属性权重协同学习[12]，以及对权重进行区间监督[13]等策略强调重要属性的作用，有效提高了完全数据集的聚类准确率.本文将属性加权的思路引入不完全数据集的模糊聚类问题，利用ReliefF算法分析各维属性的聚类贡献并结合入模糊c均值聚类，进而改善不完全数据集的聚类效果.

1 属性加权模糊c均值聚类算法

属性加权模糊c均值（weighted fuzzycmeans，WFCM）算法[10－13]将完备 数据集X＝｛x1，x2，…，xn｝Rp划分为c个模糊类，对于给定属性权重w＝（w1w2…wp）T，j：wj＞0，通常使得聚类目标函数

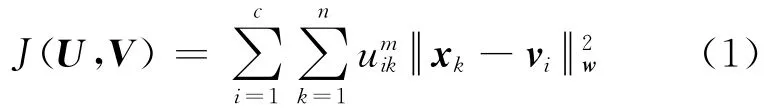
取得极小值.其中xk＝ （x1kx2k…xpk）T为样本数据；vi∈Rp为第i类的聚类中心，记V＝（vji）∈Rp×c为聚类中心矩阵；uik∈ [0，1]表示样本xk隶属于第i类的程度，且满足记U＝（uik）∈Rc×n为模糊划分矩阵；m＞1为模糊化参数表示如下加权欧式距离：

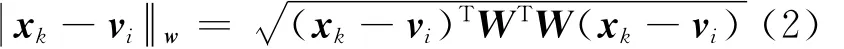
式中：W＝diag｛w1，w2，…，wp｝为对角阵.

采用拉格朗日乘子法，可得聚类目标函数取得极小值的必要条件为

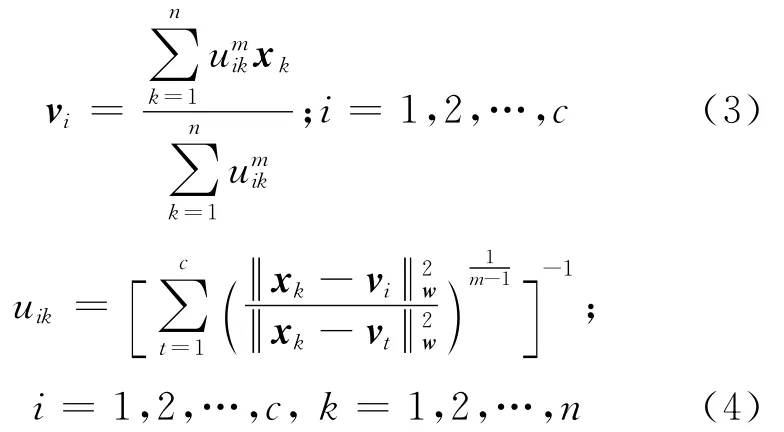
属性加权模糊c均值算法采用交替优化（alternating optimization，AO）策略对聚类目标函数（1）进行优化，当各属性权重相等时，算法为基本FCM算法.

2 ReliefF属性评价算法

Relief系列算法是基于样本类内相似性及类间相异性的属性评价方法[14，15]，最初的 Relief算法仅局限于求解两类的分类问题[15]，后扩展为ReliefF算法[14]以解决有噪声及多类问题的属性评价.

设X＝ ｛x1，x2，…，xn｝Rp为待评价的完整数据集，xk＝（x1kx2k…xpk）T，为样本数据，对于任意选取的基准样本xk（1≤k≤n），ReliefF算法首先在同类中搜索其z个最近邻样本hr（r＝1，2，…，z），然后在各不同类中分别搜索其z个最近邻样本mlr（r＝1，2，…，z；l≠class（xk）），并通过下式度量基准样本xk与近邻样本xb在第j个属性上的差异：

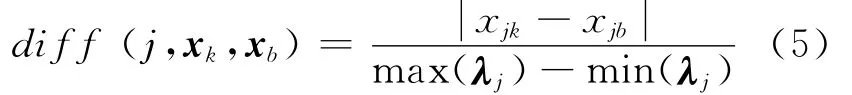
其中λj＝（xj1xj2…xjn）T，为数据集中各样本第j个属性组成的向量，max（λj）和min（λj）分别表示各样本第j个属性取值的最大及最小值.通过取nr个随机基准样本，ReliefF算法中权值由下式更新[14]：其中P（l）为第l类出现的概率.

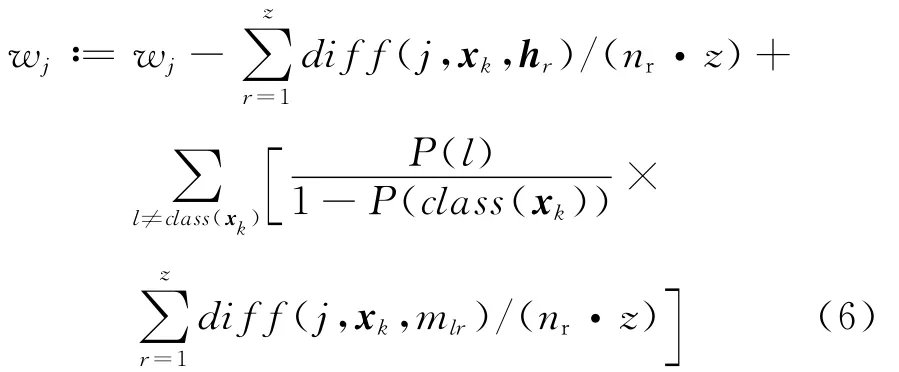
3 基于属性加权的不完全数模糊c均值聚类算法

本文采用ReliefF算法获得属性权重向量w用于无监督的不完全数据加权聚类分析，但该算法是一种有监督学习模式下的属性评价方法，即在已知样本类属的基础上评价属性的重要程度.针对完全数据集，文献[11]将有监督的ReliefF算法应用于无监督聚类分析，本文借鉴文献[11]的方法，采用如下针对不完全数据集的属性加权策略：鉴于经典的OCS－FCM算法能够同时获取数据集划分及对缺失属性的估算，因而，可首先对不完全数据集利用OCS－FCM算法进行聚类，获得样本类属及由缺失属性估算值“还原”的完备数据集，则在此基础上可通过ReliefF算法实现对属性较为合理的评价，使得将属性加权的思路引入不完全数据集的模糊聚类问题成为可能.

在已确定的属性权重基础上，本文采用如式（2）所示的加权欧式距离作为距离度量，将属性加权引入经典的OCS－FCM算法，提出了基于属性加权的不完全数模糊c均值（WOCS－FCM）聚类算法.令珟X＝｛槇x1，槇x2，…，槇xn｝为不完全数据集，WOCS－FCM算法将缺失属性作为变量优化如下目标函数：

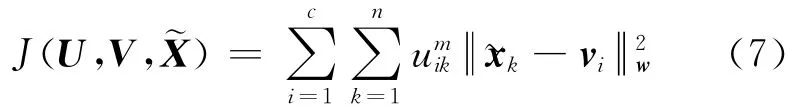
借鉴文献[3]，可得使得目标函数（7）达到极小值的必要条件为式（3）、（4）以及下式：

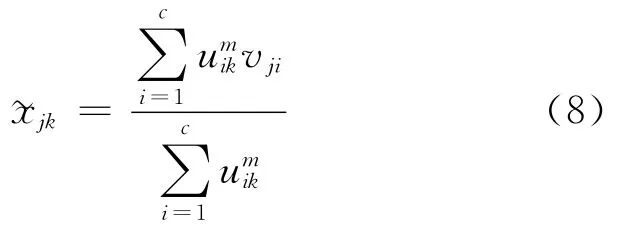
WOCS－FCM算法流程如下：

（1）利用ReliefF算法得属性权重向量w＝（w1w2…wp）T；

（2）设定聚类类别数c，设定迭代停止阈值ε，初始化缺失属性及划分矩阵U（0）；

（3）当迭代次数为l（l＝1，2，…）时，根据U（l－1），利用式（3）更新聚类原型V（l）；

（4）根据V（l），利用式（4）更新划分矩阵U（l）；

（5）利用式（8）估算缺失属性槇xjk；

4 数值实验

4.1 数据集

本文对两个著名数据集IRIS[16]及 Crude－Oil[17]进行了聚类分析，这两个数据集常被用作检验聚类算法性能的标准数据.

IRIS数据集由150个样本组成，每个样本有4个属性，分别表示IRIS的Petal Length、Petal Width、Sepal Length和Sepal Width.整个样本集包含了3个IRIS种类，分别为Setosa、Versicolor和Virginica，每类各有50个样本，其中Setosa与其他两类间能较好地分离，而Versicolor和Virginica之间存在交叠.Hathaway等[18]给出这组数据的实际类原型位置为

Crude－Oil数据集由56个样本组成，每个样本有5个属性，用于描述产自3个地区原油的化学成分.数据集中，7个样本来自 Wilhelm，另各有11个和38个样本分别来自Sub Mulinia及Upper Mulinia.

本文讨论属性随机缺失（missing completely at random，MCAR）不完全数据集的模糊聚类问题.通过人为随机舍弃完备数据集X中若干属性可得不完全数据集珟X，缺失属性的随机选取应满足下述条件[3]：

（1）数据集中任意样本槇xk至少保留一个完备属性；

（2）任意属性在数据集中至少保留一个完备值.

4.2 实验结果

为了测试 WOCS－FCM算法的聚类性能，将其与 WDS－FCM、PDS－FCM、OCS－FCM 及 NPSFCM 算法[3]对不完全IRIS、Crude－Oil数据集的聚类结果进行比较.本文中，各种聚类算法均选取模糊化参数m＝2，迭代停止阈值ε＝10－5，使用满足的划分矩阵U（0）作为初始值，相应的算法结束条件设置为并将 OCS－FCM、NPS－FCM 及 WOCS－FCM 算法中缺失属性的初始值设置为随机值.在ReliefF算法中，选取所有样本为基准样本评价属性权重，对于IRIS数据集，ReliefF算法搜索基准样本的近邻样本数z＝10；由于Crude－Oil数据集样本较少，近邻样本数取为z＝min｛各类中样本数目最小值，5｝.

在实验过程中发现，在相同的属性缺失程度（如IRIS数据缺失5%的属性值）下，数据集缺失不同的属性将可能造成聚类结果的差异.因此，为避免这种差异对算法性能评价的影响，本文在每种属性缺失程度下依4.1节中所述方法随机生成10个不完全数据集，取其聚类结果平均值用于算法分析.

以IRIS数据缺失5%属性值的情况为例，图1所示为在随机生成的10个不完全数据集（集1～10）上ReliefF算法所得各维属性权值.

由图1可以看出，当IRIS数据缺失5%的属性值时，在随机生成的10个数据集中，ReliefF算法确定属性Sepal Length及Sepal Width的权值均较大，而属性Petal Length及Petal Width的权值相对较小.因而，在 WOCS－FCM算法中，属性Sepal Length及Sepal Width的作用将通过如式（2）所示的加权欧式距离被强调，进而引导聚类过程.类似地，在其他缺失程度的不完全IRIS数据集及不完全Crude－Oil数据集上，重要属性也将获得较大权重以强调其在聚类过程中的作用.

表1及表2统计了两个数据集在不同属性缺失程度下10个不完全数据集的聚类结果平均值.由于已知如式（9）所示的IRIS实际类原型位置V＊，表1的后5列为各算法的聚类中心误差平方和，其计算如下[3]：

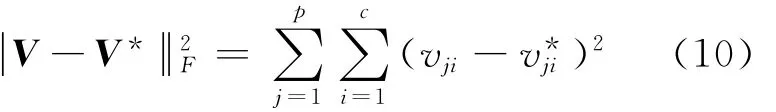
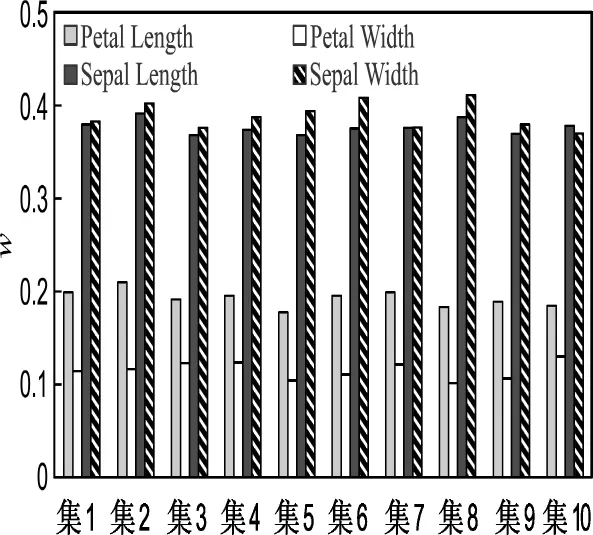
图1 IRIS数据缺失5%属性值时在10个数据集上所得各维属性权重Fig.1 The attribute weights on 10incomplete IRIS datasets with 5%attribute values missing

表1 不完全IRIS数据集的聚类结果平均值Tab.1 Averaged results of clustering using incomplete IRIS datasets

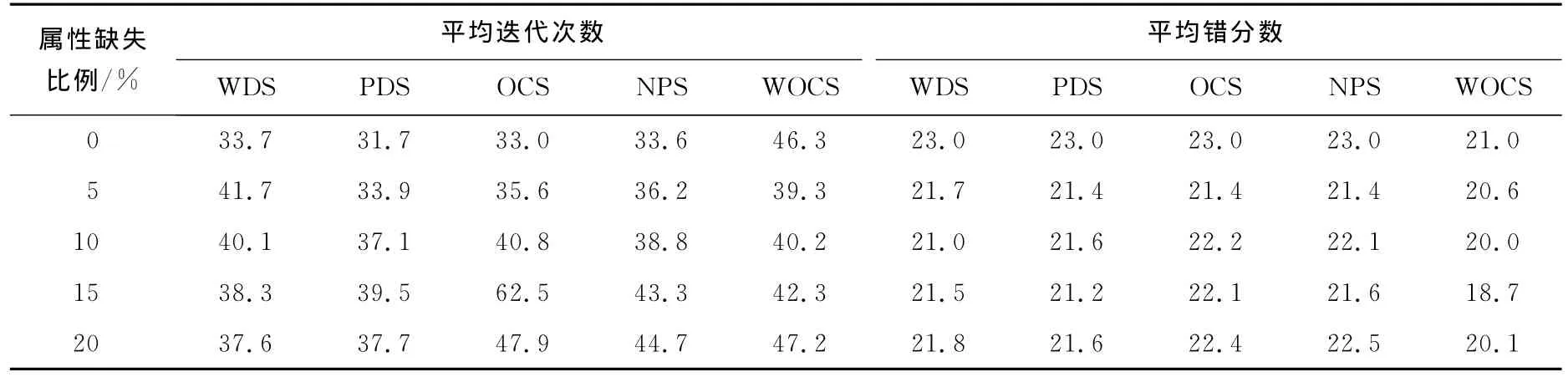
表2 不完全Crude－Oil数据集的聚类结果平均值Tab.2 Averaged results of clustering using incomplete Crude－Oil datasets

由表1、2可以看出，在不完全IRIS及Crude－Oil数据集的不同属性缺失程度下，基于属性加权的WOCS－FCM算法在迭代次数方面与其他4种算法基本相当；而在两个数据集的错分数及IRIS数据集聚类中心误差平方和方面，WOCS－FCM算法通过强调重要属性的贡献得到了更合理的数据集划分，改善了不完全数据集的聚类效果.以上结果表明本文提出的基于属性加权的模糊c均值聚类算法是合理有效的.

5 结 语

本文从强化重要属性在不完全数据集聚类分析中作用的角度考虑，提出了一种基于属性加权的不完全数模糊c均值聚类算法.该算法在ReliefF算法获得的属性权重基础上，将属性加权思路引入不完全数据集模糊聚类，能够实现对缺失属性及聚类结果的一体化求解.实验结果表明了本文所提算法的有效性和相比已有结果的优越性.下一步工作是将属性加权思路应用于部分缺失图像的处理中.

[1] Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York：Plenum Press，1981.

[2] Miyamoto S，Takata O，Uayahara K.Handling missing values in fuzzyc－means[C]//Proceedings of the 3rd Asian Fuzzy System Symposium.Seoul：Packsan Publishers Inc.，1998：139－142.

[3] Hathaway R J，Bezdek J C.Fuzzyc－means clustering of incomplete data [J].IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2001，31（5）：735－744.

[4] Timm H，Doring C，Kruse R.Different approaches to fuzzy clustering of incomplete datasets [J].International Journal of Approximate Reasoning，2004，35（3）：239－249.

[5] Hathaway R J，Bezdek J C.Clustering incomplete relational data using the non－Euclidean relational fuzzyc－means algorithm [J].Pattern Recognition Letters，2002，23（1－3）：151－160.

[6] Honda K，Ichihashi H.Linear fuzzy clustering techniques with missing values and their application to local principle component analysis [J].IEEE Transactions on Fuzzy System，2004，12（2）：183－193.

[7] Lim C P，Leong J H，Kuan M M.A hybrid neural network system for pattern classification tasks with missing features[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（4）：648－653.

[8] LI Dan，GU Hong，ZHANG Li－yong，etal.A fuzzyc－means clustering algorithm based on nearestneighbor intervals for incomplete data [J].Expert Systems with Applications，2010，37（10）：6942－6947.

[9] Dixon J K.Pattern recognition with partly missing data[J].IEEE Transactions on Systems，Man，and Cybernetics，1979，9（10）：617－621.

[10] WANG X Z，WANG Y D，WANG L J.Improving fuzzyc－means clustering based on feature－weight learning [J].Pattern Recognition Letters，2004，25（10）：1123－1132.

[11] 李 洁，高新波，焦李成.基于特征加权的模糊聚类新算法[J].电子学报，2006，34（1）：89－92.LI Jie，GAO Xin－bo，JIAO Li－cheng.A new feature weighted fuzzy clustering algorithm [J]. Acta Electronica Sinica，2006，34（1）：89－92.（in Chinese）

[12] ZHANG Li－yong，LI Dan，ZHONG Chong－quan.Collaborative optimization of clustering by fuzzycmeans and weight determination by ReliefF[C]//Proceedings of the 6th International Conference on Fuzzy Systems and Knowledge Discovery.Minneapolis：IEEE Computer Society Press，2009：454－459.

[13] 李 丹，顾 宏，张立勇.基于属性权重区间监督的模糊C均值聚类算法[J].控制与决策，2010，25（3）：457－460.LI Dan，GU Hong，ZHANG Li－yong.A fuzzycmeans algorithm with interval－supervised attribute weights[J].Control and Decision，2010，25（3）：457－460.（in Chinese）

[14] Kononenko I.Estimating attributes：Analysis and extensions of Relief[C]//Proceedings of the 7th European Conference on Machine Learning.Catania：Springer－Verlag，1994：171－182.

[15] Kira K，Rendell L A.A practical approach to feature selection [C]// Proceedings of the 9th International Conference on Machine Learning.San Mateo：Morgan Kaufmann Publishers，1992：249－256.

[16] Blzke C L，Merz C J.UCI repository of machine learning databases [EB/OL]. [2010－02－12].http：//www. ics. uci. edu/～ mlearn.MLResitory.html.

[17] Johnson R A，Wichern D W.Applied Multivariate Statistical Analysis[M].New Jersey：Prentice－Hall，1982.

[18] Hathaway R J，Bezdek J C. Optimization of clustering criteria by reformulation [J].IEEE Transactions on Fuzzy Systems，1995，3（2）：241－245.