基于粒子群算法的大跨度钢结构吊点层次优化

王 欣， 陈 博 文， 林 远 山， 高 顺 德

（1.大连理工大学 机械工程学院，辽宁 大连 116024；2.大连理工大学 计算机科学与技术学院，辽宁 大连 116024）

0 引 言

随着各种复杂大跨度钢结构建设项目的增多，以及整体吊装技术的逐渐应用，人们对大跨度钢结构的吊装技术及吊装过程中表现的诸多力学及技术问题愈来愈重视.对于多台起重机整体吊装时各吊点的设计就是其中一个关键性的问题，要求其在保证吊装过程中结构不发生失稳或较大变形的同时合理分配各起重机所承担的荷载.

针对多吊点设计问题，工程中多是以简单的力矩平衡分析吊点受力对其进行设计；文献[1]将吊装设备等效成均匀的板结构或者梁结构，对其进行相关公式推导，求得弯矩、频率极值状态下的吊点位置；文献[2]则忽略结构变形对起重机受力的影响，将钢结构当作纯刚体处理，以多台起重机的综合负荷率最小为目标函数，求解满足力矩平衡约束条件下的各吊点位置的最优解；文献[3]通过钢结构有限元模型，利用APDL语言编制优化算法，遍历各种吊点组合工况下结构的应变能，以最小应变能工况下对应的吊点位置为最优解.

这些研究离真正的工程应用尚有一定的距离，具体表现在：（1）大跨度结构型式复杂，分布不均匀，将其简单等效成理想状态下的板、梁结构求解出的吊点位置不具有实际参考意义；（2）大跨度结构重量、体积较大，吊装过程中设备变形较大，而由变形导致的各起重机受力差距也较大，因而忽略结构变形，只追求起重机综合负荷率最小工况下的吊点位置与实际误差较大；（3）为满足吊装过程中的平稳性，大跨度吊点数量较多，考虑到吊装强度要求多设置在主梁交叉点处，即吊点位置离散分布，如果要遍历所有吊点组合工况下的吊点位置，则效率太低.且文献中均只考虑位置布局，未谈及数量优化问题.

本文将粒子群算法应用于大跨度钢结构吊点优化设计当中，建立求解的适值函数和惩罚策略，并提出对数量和位置进行层次优化的策略.为了使该方法进一步实用化，通过APDL语言建立钢结构参数化的有限元模型，并将ANSYS应用到粒 子 群 算 法 （particle swarm optimization，PSO）[4]的适值计算当中，通过将标准粒子群算法进行改进并结合APDL的ANSYS二次开发技术，编制适应于大跨度钢结构吊点优化设计的程序，并与ANSYS自带的零阶算法以及遗传算法、模拟退火算法等先进优化算法相比，通过算例证明改进的粒子群算法在多吊点离散变量优化中的能力和本文程序的实用性与通用性.

1 钢结构吊点体系设计

在大跨度钢结构吊装过程中，吊点的合理布置改善了结构在吊装过程中的受力性能，降低了挠度，从而使吊装实施更为科学与安全.吊点体系的设计面临3个问题：首先是吊点数量的确定，吊装时需要根据荷载条件和现场要求决定；其次是吊点的位置布置，以使结构在吊装过程中处于较好的受力状态；最后则是起重机起重性能的考虑，通过吊点数量分配起重机所受荷载，并留有一定的安全裕度.如何在满足结构安全要求的基础上选择一种最优的吊点体系，是一个亟待研究的问题，具体如图1所示.

图1 大跨度钢结构吊点体系布局图Fig.1 Distribution of lift points system of largespan steel structure

1.1 能量方法在吊点体系设计中的应用

在弹性材料体内，如果略去加载和卸载过程中的能量损耗，外力所做的功W在数值上就等于积蓄在弹性材料体内的应变能U.如果取出一个边长为单位长度的单元体，则作用在该单元体上、下两表面上的力为σ，单元体伸长量为ε，即

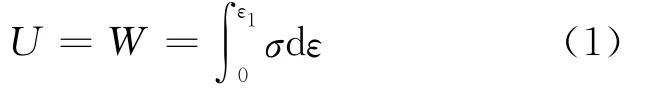
在有限元结构计算当中，因为结构本身或者建模方式的不同会存在应力集中现象，故不能取整体结构的最大应力作为吊点设计好坏的判定条件.但从宏观角度来看，变形以及应力可以体现在结构整体或者单元的应变能上.故在本文中，以整体结构最小应变能这一量化指标作为评判吊点体系设计合理性的标准.

1.2 吊点体系设计方法

对于单根直梁吊装而言，吊点可通过求解弯曲应变能方程的极值状态来获得，而实际工程中的复杂结构很难通过解析方法求得最优吊点，此时一种可行的解决方案是基于数值方法求解在不同吊点体系下的结构应变能，并采用先进的优化方法搜索最佳的吊点体系.

2 粒子群算法及其程序实现

粒子群算法是一种全局最优化方法，它源于对鸟群和鱼捕食行为的模拟，且操作较遗传算法简单，具有可并行搜索、可求解不可微分方程且无需方程梯度信息等优点，正成为继遗传算法、模拟退火算法之后优化领域研究的新方向.

2.1 吊点优化分析

2.1.1 设计变量选取 在吊点优化中，整个钢结构上的吊点数量和布局直接影响着结构本身在吊装过程中的强度和稳定性，因此选择吊点数量和位置为寻优粒子——设计变量.

2.1.2 设计变量的变换 设计变量的变换即对应粒子位置的改变，在粒子群算法中，通过更改粒子速度和方向来修改粒子所在位置，具体方法如式（2）、（3）所示，其中w为惯性权重，它决定了粒子的基本速度，为了使算法更灵活，按式（4）来设定w，从而完成从大范围到局部的深层搜索.而在吊点优化中，设计变量的变换即对应一组新的离散吊点位置的产生，在全局范围内随机产生一批吊点位置，根据计算的全局极值总体上确定吊点位置最优区域，然后减小搜索步长，最终确定最优吊点，这也是粒子群算法更适合应用于吊点优化的原因所在.

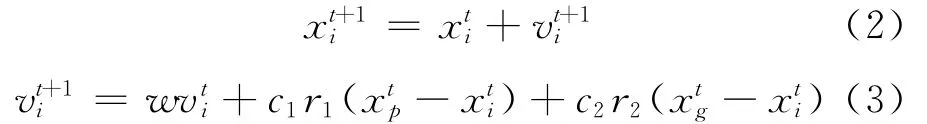
式中：wmax取0.9，wmin取0.4，n为当前迭代次数，nmax是总的迭代次数.r1、r2为[0，1]的随机数；c1、c2为两个学习因子，一般取值范围为[0，2]，常取固定值为粒子p在自身更新t轮中最好的位置，被称为为粒子群中t次更新出现的最好粒子位置，被称为gbest.

2.1.3 适应度函数的确定 每次变换粒子位置都要重新求解粒子的个体极值和全局极值，粒子位置的改变都以其适应值为判定依据，当满足停止准则时，搜索结束，因而适应度函数的合理确定是保证计算精度的关键.

将多吊点优化定义成状态变量满足一系列等式或不等式约束前提下的最优化目标函数的非线性规划问题求解，且起重机受力要满足在其许用荷载范围之内的约束条件，如钢丝绳及机构的承载能力.因而本文拟将粒子群算法与惩罚函数法相结合[5]，将不满足约束条件的点淘汰.

多吊点优化数学模型为

式中：E（x，y）为结构整体应变能，x表示吊点个数，y表示吊点位置；g（x，y）为根据吊点个数、位置计算所得ANSYS数值结果；Fi（x，y）为各起重机的实际受力；[Fi]为各起重机的许用荷载；Ni（x，y）为吊点编号，k为吊点编号总数，N为待选吊点集.

针对粒子群算法构造的基于惩罚函数的适应度函数如式（6）所示：

式中：eval（x，y）为粒子群算法的适应度函数；r为约束惩罚因子，一般为目标函数最优值的1～10倍；sφ（x）中s为离散惩罚因子，φ（x）为离散惩罚函数.

式（6）中约束惩罚函数是根据文献[6]中的外惩罚函数建立的，离散惩罚函数的建立文献[7]中有专门的介绍，本文中所要研究的设计变量吊点个数和吊点位置均为正整数或者正整数的组合形式，可直接将随机得出的设计变量圆整，无需修改适应度函数，减少因连续变量造成的不必要的惩罚函数计算，提高优化效率.故离散惩罚项sφ（x）取0.

2.2 基于粒子群算法的吊点层次优化程序

将粒子群算法应用于大跨度钢结构吊点层次优化时，流程图如图2所示.整个程序是在MATLAB编译环境中编写的，将粒子群算法进行改进并结合APDL对ANSYS的二次开发，后台运行ANSYS有限元软件求解目标函数（最小应变能）来实现.

图2 粒子群算法多吊点优化流程图Fig.2 Flow chart of multiple lift points optimization using particle swarm optimization

吊点优化包含数量和位置的同时处理，而结构应变能（目标函数）又是在给定吊点数量和位置的情况下计算所得，因而本文将粒子群算法分为两个层次来对吊点进行优化，第一层也是最外层用于完成吊点数量的优化，而里层则用来对位置进行优化.吊点数量的优化是以前后两次的结构应变能变化小于给定的任意小值为收敛条件.为了保证寻优效率，在进行吊点数量优化过程中，对其里层进行的吊点位置优化设置较少的粒子群个数和迭代次数进行搜索，而对完成吊点个数优化之后的吊点位置深度优化时，再增大粒子群个数和迭代次数.这样做的原因是考虑到在一定迭代次数下，算法已趋于收敛，在这种情况下不同吊点数量对应的结构应变能差值，即｜gbesti－gbesti＋1｜已变化不大，能够代表一定吊点数量情况下最优吊点位置的结构应变能，通过这样的迭代准则不但提高了寻优效率，同时也保证了求解的精度.

关于结构应变能的计算是通过建立参数化的命令流文件供MATLAB后台调用来完成的，可提高求解速度.

3 计算实例

对如图3所示的海洋平台甲板片进行多吊点优化.

图3 海洋平台甲板片有限元模型Fig.3 Finite element model of ocean platform deck

该甲板为片状结构，长近41m，宽约11m，整体自重约为91t.其中，板梁组合结构在有限元中通过重合节点方式传递受力.由图3可知，该甲板片由3排7列主梁组成，故有21个备选吊点位置，将其进行编号，如图所标注.

3.1 吊点层次优化结果

根据所提出基于粒子群的层次优化方法，选取粒子群初始值为30，迭代次数为15，惯性权重按0.9到0.4递减，最大速度为100，学习因子c1、c2均为2，收敛条件为迭代前后最小应变能差值102J.对吊点数量和位置进行优化，优化结果：最优吊点位置为（2，11，7，16，18），最优吊点数量为5，最小应变能为1.59×104J.

图4给出了4吊点（曲线1）和5吊点（曲线2和3）的优化求解过程.其中5吊点在满足收敛条件下，进行了精细二次优化（增加粒子群），优化过程表现为2条曲线（曲线2和曲线3）.由此看出，深度寻优是有条件的，可提高优化速度.

图4 吊点层次优化最优解图Fig.4 Optimal solutions to hiberarchy optimization of lift points

3.2 优化算法对比分析

为了证实本文算法的有效性，采取了4种方法进行对比分析：枚举法、ANSYS有限元软件自带的零阶算法、遗传算法及模拟退火算法.其中枚举法进行所有吊点的遍历，可以获得极值，来验证本算例结果的有效性.

4种算法是在 Windows XP（2GB RAM/2GHz CPU）的微机上运行的，最优吊点数量都是5，表1给出此吊点数量下的最优吊点位置，各起重机许用荷载均为2.5×105N.吊点位置组合共有种工况，因此枚举法计算时间最长，达到784min，但可获得极值，对应的最小应变能为1.58×104J.其他4种算法（包括本文提出的粒子群算法）计算时间较短，优化结果对应的最小应变能则差别较大，其中本文算法的数值最接近极值（枚举法结果），差异最小，计算时间略长.由此看出本文提出算法的有效性与合理性.

表1 5吊点最优位置布置工况Tab.1 Working conditions of 5lift point optimal location distribution

4 结 语

本文在分析和建立吊点体系设计的基础上，提出基于粒子群的层次优化策略来对吊点数量和吊点位置同时寻优，建立了以起重机负荷率为约束条件，以结构整体最小应变能为目标函数的优化数学模型.层次优化的策略是：里层基于粒子群算法进行吊点位置优化，外层进行吊点数量优化.实例分析及与其他算法的结果比较，表明了本算法在优化结果和计算时间上的有效性和合理性.

该方法除应用于平面钢结构，还为空间钢结构的吊点设计提供了参考思路，但搜索时间略长，后续工作将研究如何对整个解空间进行区域划分，减少非可行解计算造成的时间浪费，并分析问题规模和粒子群大小以及迭代次数的关系，从而设置更合适的寻优参数.

[1] Rajasekaran S，Annet D，Sang Choo Y.Optimal locations for heavy lifts for offshore platforms[J].Asian Journal of Civil Engineering（Building and Housing），2008，9（6）：605－627.

[2] 胡尚礼.多台履带式起重机协同作业研究[D].天津：天津大学，2007.HU Shang－li.Research on the cooperation of several crawler cranes [D].Tianjin：Tianjin University，2007.（in Chinese）

[3] 张 冰.大跨度空间结构建造过程中吊点和支撑位置合理性研究[D].杭州：浙江大学，2006.ZHANG Bing.Research on layout of hoisting and temporary support in the construction process of long－span space structures[D].Hangzhou：Zhejiang University，2007.（in Chinese）

[4] 于 颖，李永生，于孝春.粒子群算法在工程优化设计中的应用[J].机械工程学报，2008，44（12）：226－231.YU Ying， LI Yong－sheng， YU Xiao－chun.Application of particle swarm optimization in the engineering optimization design[J].Chinese Journal of Mechanical Engineering，2008，44（12）：226－231.（in Chinese）

[5] HE S，Prempain E，WU Q H.An improved particle swarm optimizer for mechanical design optimization problems [J]. Engineering Optimization，2004，36（5）：585－605.

[6] Shind K. A penalty approach for nonlinear optimization with discrete design variables [J].Engineering Optimization，1990，16（1）：29－42.

[7] JUAN J.Particle swarm optimization applications in power system engineering [D]. Puerto Rico：University of Puerto Rico，2004.

[8] 博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京：中国水利水电出版社，2004.Game Studio.Parametric Finite Element Analysis Technology and Its Application Based on APDL[M].Beijing：China Water Conservancy and Hydropower Press，2004.（in Chinese）

[9] 马劲红，张文志，宋剑锋，等.MOGA和FEM相结合实现万能型钢轧机机架圆角的多目标优化[J].塑性工程学报，2008，15（1）：146－149.MA Jin－hong，ZHANG Wen－zhi，SONG Jian－feng，etal.Multi－objective optimization of the housing′s fillet angle of the universal rolling mills using MOGA combined with FEM [J].Journal of Plasticity Engineering，2008，15（1）：146－149.（in Chinese）

[10] 朱劲松，高嫦娥，肖汝诚.基于遗传算法的结构损伤识别及其程序设计[J].哈尔滨工业大学学报，2007，39（12）：1952－1956.ZHU Jin－song，GAO Chang－e，XIAO Ru－cheng.Identification of damage in structures using genetic algorithms and programming[J].Journal of Harbin Institute of Technology，2007，39（12）：1952－1956.（in Chinese）

[11] 范小宁，林 焰，纪卓尚.基于自适应退火遗传算法的船舶管路布局优化方法[J].大连理工大学学报，2007，47（2）：215－221.FAN Xiao－ning， LIN Yan， JI Zhuo－shang.Approach of ship pipe paths routing optimization based on adaptive annealing genetic algorithm [J].Journal of Dalian University of Technology，2007，47（2）：215－221.（in Chinese）