有色噪声背景下自适应雷达波形优化设计
庄珊娜 贺亚鹏 朱晓华
(南京理工大学电子工程与光电技术学院,江苏 南京 210094)
引 言
雷达是通过对目标回波的处理进行检测、跟踪和识别的,而发射波形的选取会影响目标回波中信息的提取,因此,优化发射波形对雷达目标的检测和识别均具有非常重要的意义[1-6]。针对目标环境中有色噪声的统计特性自适应设计一组具有较低距离旁瓣和峰均比(PAPR)的发射波形,不仅可抑制有色噪声,提高目标检测性能,还能降低微弱信号被强信号距离旁瓣掩盖的机率,同时降低系统复杂度,提高发射机的功率利用率,这对提高现代雷达的战场适应力具有重要的军事价值。
在统计特性已知的有色噪声背景下,通过优化发射波形,雷达能够显著提高匹配滤波器的输出信噪比(SNR),增强检测性能。Chen[7]提出了在已知扩展目标和杂波先验信息的情况下,联合优化MIMO雷达的发射波形和接收端滤波器的迭代算法,该算法收敛速度快且能获得较好的检测性能。Friedlander[8]构建了信号子空间来设计优化波形,使得在已知目标、杂波和噪声的统计特性的条件下,最大化检测器输出SNR,改善检测性能。但文献[7][8]仅优化检测SNR,忽略了波形自身性能,导致所优化波形自相关主旁瓣比过低,PAPR较高。针对该问题,Bergin[9]和Li[10]利用有色噪声协方差矩阵的奇异性,提出了选取一组与有色噪声无关的特征向量,对其加权逼近于某一预先设定的波形,使得SNR提高的同时波形性能接近于该预定波形。Maio[11]提出了一种相位编码算法,使得在有色高斯噪声中提高检测性能,同时,使所优化波形的模糊函数逼近某一预先设定的雷达编码信号,从而在一定范围内获得满意的距离、多普勒分辨率。然而文献[9]-[11]所优化波形性能受限于预先设定波形,灵活性较差,且会带来较大SNR损失,降低检测性能。
为解决上述问题,提出目标信号子空间加权(WTSS)法自适应设计发射波形,该方法能有效抑制有色噪声,提高雷达检测性能,同时获得较好的自相关性和PAPR,且无需预先设定波形,灵活性高。首先,给出有色噪声中目标检测的系统模型及最大化检测SNR的波形优化方法,选取一组目标-有色噪声(TCN) 矩阵的大特征向量,对其标准正交化作为基构成目标信号子空间,通过对该子空间加权选取满足相关性和PAPR约束的优化波形,建立目标函数搜索加权系数,并采用序列二次规划(SQP)算法对其求解。仿真结果验证了该方法的有效性。
1. 有色噪声中目标检测的系统模型


图1 系统模型图
因此系统输出为
y=hHr=hHsR+hHn=ys+yn
(1)
式中:ys为目标分量;yn为有色噪声分量,分别定义为
ys=hHsR
(2)
yn=hHn
(3)
假设发射信号与有色噪声相互独立,则回波的协方差矩阵表示为
Rr=E[rrH]=Rs+Rn
(4)
式中:E[·]为期望算子;Rs和Rn分别为发射波形和有色噪声的协方差矩阵,定义如下
(5)
Rn=E[nnH]
(6)
根据式(2)~(6),系统输出端SNR为
(7)
使式(7)中γ最大化的最优接收滤波器为[12]
(8)
不失一般性,令α=1,将式(8)代入式(7),得最优接收滤波器下的最优SNR为
(9)
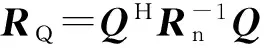
2. WTSS法优化发射波形
以umax作为雷达发射波形,可使检测SNR最大化,但往往存在波形自相关主旁瓣比低、PAPR高等问题。针对上述问题,WTSS法对TCN矩阵特征分解,选取大特征向量构成目标信号子空间,通过优化加权系数在其中选取最优发射波形,使得仅以较小的SNR损失为代价,在有效抑制有色噪声的同时自相关性能和PAPR获得较大改善。
2.1 目标信号子空间的选取
已知信号的功率谱密度,可通过式(10)获得其协方差矩阵[13]。假设信号长度为N,频谱范围为[f1,f2],其功率谱有Nb个通带,第k个通带的起始频率为fk1,截止频率为fk2, 则其N×N维协方差矩阵第m(m=1,2,…,N) 行第l(l=1,2,…,N)列元素rml为
(10)
式中:ξ(f)=exp[2πi(m-l)fΔt];ωk为相应的加权系数; Δt为采样间隔; Δt=1/(f2-f1).雷达系统在无目标时探测可获得雷达环境中有色噪声的功率谱密度,可利用式(10)获得其协方差矩阵Rn,获得TCN矩阵RQ.假设λ1≥λ2≥…≥λN为RQ的特征值,v1,v2,…,vN为其对应的特征向量。选取M个大特征值对应的特征向量vk(k=1,2,…,M),对其标准正交化得到uk(k=1,2,…,M),则{u1,u2,…,uM}构成目标信号子空间的正交基,通过加权获得所需波形,即
(11)

特征向量个数M值的选取可采用信息论法、平滑秩法、矩阵分解法、盖氏圆法以及正则相关法等[14],其中平滑秩法和矩阵分解法误差概率较高,盖氏圆法稳定性较差,正则相关法计算复杂度较高,因此这里采用误差概率较小且计算复杂度较低的信息论法,选取使

(12)
最小的M值作为目标信号子空间基的个数。式(12)中第一项为(N-M)个小特征值算术平均与几何平均的对数似然比,第二项为基于最小描述长度准则的罚函数,因此,使式(12)最小化即可获得TCN矩阵RQ不相关特征向量个数M值的一致性估计[16],从而确定目标信号子空间基的个数。
2.2 建立满足约束条件的目标函数
仅以最大化检测SNR作为目标优化的发射波形,通常具有较高的距离旁瓣和PAPR.这将导致微弱信号容易被掩盖,所需收发系统的动态范围增大等,从而降低雷达的整体性能。为克服上述缺陷,WTSS法在抑制有色噪声的同时,对波形的自相关特性和PAPR加以约束,使所优化波形具有更为良好的性能。
发射信号sT=[s1,s2,…,sN]T的自相关函数为
(13)
令l=0,得主瓣幅值为
(14)
即信号自相关函数的峰值为常数,为获得高主旁瓣比,则要求其旁瓣尽可能低,在此以积分旁瓣电平( ISL)作为衡量标准,即
(15)

考虑到实际工程应用,为降低收发系统的动态范围和复杂度,提高发射机的功率利用率,发射波形应具有较低的PAPR.信号PAPR定义为信号功率峰值与均值的比,即
(16)

(17)
式中:α=N/E为常数;‖·‖∞为向量的∞范数。若系统可接受的PAPR为p≥1,则有
α(‖sT‖∞)2 (18) 根据式(11)、(15)和(18)可建立在提高检测SNR的同时降低波形自相关旁瓣和PAPR的目标函数为 (19) SQP算法通过求解一系列的二次规划(QP)子问题获得原问题的最优解,具有全局收敛性,其收敛速度快、可靠性高、适应能力强[17]。普遍认为该方法是求解非线性约束最优化问题十分有效的方法,被广泛应用于工程优化问题的求解。 令U=[u1,u2,…,uM],α=[α1,α2,…,αM]T,则式(19)可表示为 s.t.c1(α)=‖α‖2-E=0 (20) c2(α)=q-‖Uα‖∞≥0 式中:‖·‖2为向量2范数。基于SQP算法求解目标函数式(20)步骤归纳如下: 步骤 2: 求解二次规划子问题 mindT s.t.c1(α(k))+dTc1(α(k))=0 (21) c2(α(k))+dTc2(α(k))≥0 得到d(k)及其对应的拉格朗日乘子β(k+1). 步骤 3: 采用增广拉格朗日函数作为效益函数,从点α(k)沿方向d(k)进行线性搜索确定步长γk,并令α(k+1)=α(k)+γkd(k). SQP算法的计算量主要集中在QP子问题式(21)的求解上,因此其计算复杂度为O(M3)[18]。步骤 3中选择增广拉格朗日函数作为效益函数,使得对充分大的k有γk=1,即α(k+1)=α(k)+d(k).又由文献[19]得,目标函数下降方向d(k)满足 (22) 式中:αopt为目标函数的全局最优解。因此,采用SQP算法求解式(19)中目标函数具有超线性收敛性[17]。 为验证WTSS法的有效性和优越性,下文给出计算机仿真,针对点目标和扩展目标两种目标模型,从波形抑制有色噪声的性能、自相关主旁瓣比及PAPR三方面与文献[10] SWORD法优化波形和无自相关及PAPR约束波形(即TCN矩阵RQ最大特征值对应的单位特征向量,下文简称无约束波形)相比较。 实验1:目标模型为点目标,采样点数N=100,采样间隔Δt=1/B,系统带宽B=25 MHz,其中15~18 MHz处存在有色噪声,系统可承受的PAPR为3.实验中三种波形的功率谱密度和自相关特性分别如图2、图3所示。 从图2可看出:在15~18 MHz频带处,SWORD法获得-56.55 dB左右的零陷,而WTSS法可形成-141.21 dB左右的零陷,可更有效地抑制有色噪声。与无约束波形相比WTSS法优化波形的零陷较浅,这是由于需要兼顾相关性和PAPR,以较小的SNR损失换取自相关性能和PAPR的较大改善。由图3可知,与SWORD法优化波形和无约束波形相比,WTSS法优化波形的自相关旁瓣最低,微弱信号被掩盖的机率最小,检测性能最佳。 实验2:有色噪声所处的频带分别为5~7 MHz、10~12 MHz及15~16 MHz,其余仿真条件同实验1.仿真得出,WTSS法优化波形的PAPR为2.70,分别比SWORD法优化波形和无约束波形低17.36%和15.45%.由图4可看出,在有色噪声频带数增多的情况下,WTSS法优化波形和无约束波形对有色噪声的抑制程度均明显优于SWORD法优化波形。图5给出了三种波形的自相关特性曲线,WTSS法优化波形的自相关旁瓣低于SWORD法优化波形和无约束波形的自相关旁瓣,自相关性能最优。 实验3:若目标为扩展目标,其高分辨率一维距离像模型如图6所示。其余仿真条件同实验1。由于受到目标脉冲响应的影响,既需要抑制有色噪声,减少波形能量在有色噪声频带处的分布,又要与目标的脉冲响应相匹配,使波形能量集中在目标能量较大的频带处,因此,在该仿真实验中,三种波形均不能在有色噪声频带处形成明显的零陷,这里不再给出其功率谱密度图。从SNR的角度看,WTSS法的SNR损失比SWORD法低 8.92 dB,因此,可更有效地抑制有色噪声。 图6 目标一维高分辨率距离像 图7给出了三种波形的自相关特性,与SWORD法相比,WTSS法所优化波形的旁瓣较低,自相关性能较好。与无约束波形相比,虽然WTSS法优化波形离主瓣较远处的距离旁瓣较高, 但其主瓣附近的旁瓣较低,且主瓣较窄,由于主瓣附近的旁瓣对邻近目标分辨能力的影响较大,因此,WTSS法优化波形的距离分辨力较佳,可见,WTSS法优化波形的自相关性能最优。 以上各实验中三种波形的主旁瓣比、PAPR以及SNR损失具体数值分别如表1所示。就PAPR而言,SWORD法优化波形和无约束波形的PAPR均超出了系统可承受范围,WTSS法优化波形的PAPR最低,且符合系统要求。从各实验中三种波形的主旁瓣比值可以看出,WTSS法优化波形的主旁瓣比最高,微弱信号被掩盖的几率最小。与SWORD法相比,WTSS法在抑制有色噪声、提高自相关主旁瓣比和降低PAPR三方面均较优。与无约束波形相比,WTSS法仅以较小的SNR损失换取波形自相关性能和PAPR的较大改善,达到SNR与波形自相关性能和PAPR间的良好折中,有利于提高雷达系统的整体性能,适合实际工程应用。 表1 各实验中三种波形的主旁瓣比、PAPR 图8给出了上述三个实验中目标函数的收敛曲线。从图中可看出:实验1、实验2和实验3中目标函数分别经过267、218和351次迭代后收敛。实验2中有三段频带含有色噪声,可从TCN矩阵中提取的目标信号子空间基的个数较少,即M值较小,因此求解目标函数的运算量相对于实验1和3较小,目标函数收敛速度较快,但损失了波形设计的自由度,优化所得目标函数值较大,既波形自相关旁瓣较高。SQP算法运算量较大,不能实时优化波形,实际运用中,可预先对无目标环境进行探测,根据多种可能出现的雷达场景设计发射波形,形成最优波形库,供雷达系统根据实际环境自适应选择所需波形。 图8 目标函数收敛曲线 基于目标信号子空间优化加权系数设计发射波形能够有效地抑制有色噪声,提高匹配滤波器输出SNR,优化检测性能,同时降低波形的距离旁瓣,减小微弱信号被掩盖的机率,并保证PAPR在雷达系统可接受的范围内,降低收发系统的动态范围,适合实际工程应用。相比仅以最大化SNR为目标优化波形,WTSS法优化波形具有更优的性能,雷达的整体性能得到提高,适应性增强。同时WTSS法可根据实际战场环境自适应设计所需功率谱,并可单独设置约束条件,同逼近预先设定波形相比,该方法灵活性较强。 [1] 黎薇萍, 陶海红, 廖桂生, 等. 抗干扰多波形优化设计技术[J]. 电波科学学报, 2010, 25(5): 940-946. LI Weiping, TAO Haihong and LIAO Guisheng, et al. Multi-waveform optimal design technique against repeat radar jammers [J]. Chinese Journal of Radio Science, 2010, 25(5):940-946. (in Chinese). [2] 纠 博, 刘宏伟, 何学辉, 等. 基于凸优化的宽带雷达波形优化设计 [J]. 电波科学学报, 2009, 24(2):265-269. JIU Bo, LIU Hongwei and HE Xuehui, et al. Method of broadband radar waveform design based on convex optimization [J]. Chinese Journal of Radio Science, 2009, 24(2):265-269. (in Chinese) [3] 董志飞, 陈泽宗, 柯享玉, 等. 近海回波压制远程高频地波雷达波形设计 [J]. 电波科学学报, 2006, 21(4):558-581. DONG Zhifei, CHEN Zongze and KE Xiangyu, et al. Waveform design for long-range HF ground wave radar with offing sea-echo suppression [J]. Chinese Journal of Radio Science, 2006, 21(4):558-581. (in Chinese). [4] GUERCI J R. Constrained optimum matched illumination-reception radar: USA, 5146229[P]. 1992-09-08. [5] GARREN D A, OSBORN M K, ODOM A C, et al. Enhanced target detection and identification via optimized radar transmission pulse shape [J].IEE Proc.-Radar, Sonar and Navigation, 2001, 148(3):130-138. [6] PILLAI S U, OH H S, GUERCI J R, et al. Optimum transmit-receiver design in the presence of signal-dependent interference and channel noise [J]. IEEE Transactions on Information Theory, 2000, 46(2):577-584. [7] CHEN C Y, VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter [J]. IEEE Transactions on signal processing, 2009, 57(9):3533-3544. [8] FRIEDLANDER B. A subspace framework for adaptive radar waveform design[C]//Conference Record of 39th Asilomar Conference on Signals, System and Computers. Pacific Grove, CA, 2005:1135-1139. [9] BERGIN J S, TECHAU P M, GUERCI J R, et al. Radar waveform optimization for colored noise mitigation[C]//IEEE International Radar Conference. Alexandria, VA, USA, 2005:149-154. [10] LI J, GUERCI J R, XU L Z. Signal waveform's optimal-under-restriction design for active sensing [J]. IEEE Signal Processing Letters, 2006, 13(9): 565-568. [11] MAIO A D, NICOLA S D, HUANG Y W, et al. Design of phase codes for radar performance optimization with a similarity constraint [J]. IEEE Transactions on Signal Processing, 2009, 57(2):610-621. [12] RICHARDS M A. 雷达信号处理基础[M].刑孟道, 王彤, 李真芳,等译. 北京:电子工业出版社,2008. RICHARDS M A. Fundamentals of radar signal processing[M]. XING Mengdao, WANG Tong, LI Zhenfang, et al translation. Beijing: Publishing house of electronics industry, 2008. (in Chinese). [13] LINDENFELD M J. Sparse frequency transmit and receive waveform design [J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3):851-860. [14] 王永良, 陈 辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004. WANG Yongliang, CHEN Hui, PENG Yingning, et al. Spatial spectrum estimation theory and algorithm[M]. Beijing: Tsinghua University Press, 2004. (in Chinese). [15] 叶中付, 向 利, 徐 旭. 基于信息论准则的信源个数估计算法改进[J]. 电波科学学报, 2007, 22(4):593-598. YE Zhongfu, XIANG Li, XU Xu. Improvement of source number estimation based on information theoretic criteria [J]. Chinese Journal of Radio Science, 2007, 22(4):593-598.(in Chinese). [16] Max M, Kailath T. Detection of Signals by Information Theoretic Criteria [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, ASSP-33(2):387-392. [17] 徐成贤, 陈志平, 李乃成. 近代优化方法[M]. 北京:科学出版社, 2007. XU Chengxian, CHEN Zhiping, LI Naicheng. Modern optimization methods [M]. Beijing: Science press, 2007. (in Chinese). [18] 周晓飞, 姜文瀚, 杨静宇. 核子空间样本选择方法的核最近邻凸包分类器 [J]. 计算机工程应用, 2007, 43(32):34-37. ZHOU Xiaofei, JIANG Wenhan, YANG Jingyu. Kernel nearest neighbor convex hull classifier with kernel subspace sample selection method [J]. Computer Engineering and Applications, 2007, 43(32): 34-37. (in Chinese). [19] 袁亚湘, 孙文瑜. 最优化理论与方法 [M]. 北京:科学出版社, 1997. YUAN Yaxiang, SUN Wenyu. Optimal theory and method [M]. Beijing: Science press, 1997. (in Chinese).

2.3 基于SQP的波形优化设计
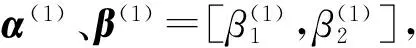
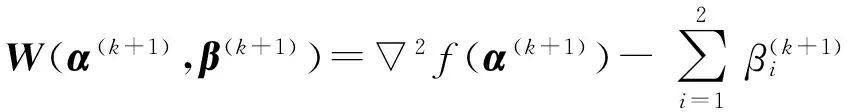
3. 仿真结果及分析



4. 结 论

