电网负荷特性分析与预测

陈茂迁，王海燕，陈仕军

（1.宁波电业局，浙江 宁波 315800；2.眉山电力公司，四川 眉山 620010）

0 引言

负荷特性[1]曲线的波动性与年最大负荷、日最大负荷出现的时间有关，而影响负荷曲线形状的主要因素是负荷的季节变化、用电设备的大修情况及负荷在年内的增长情况。

文献[2-10]分别对广州、南京、上海等地的负荷特性进行详细分析和说明，指出了这类地区负荷特性的影响因素和发展趋势，符合当地的实际情况，但是其分析过程不适宜推广到其他地区或城市。

负荷特性的预测与分析通常采用统计学原理来进行，但是数据分析相当困难，要从大量的数据中找出各种周期性的规律,得出与预测相关因素的大小与权值,并根据这些数据来预测未来的负荷。本文提出了一种简化的负荷特性分析与预测的算法，在现状分析的基础上，对某一实际地区未来5年和10年的负荷特性进行预测。

1 现状分析

在对负荷现状作分析时，要综合利用多年的数据，但这些数据事先必须进行处理和修正。

1.1 基础数据

基础数据是分析的基础，必须准确地收集多年资料，A代表基础数据的整体，其中Xn为每组数据的多年值，即：

其中：xn（t）在年负荷特性中为第t年每个月份的负荷最大值，在日负荷特性中为第t年典型日每个时刻点的负荷最大值；t为年份；n在年负荷特性中为12，在日负荷特性中为24。

1.2 基础数据标幺化

多年数据的数值大小差别很大，可比性较差，因此需要对基础数据进行标幺化处理。

年度数据的最大值 Xmax（t）：

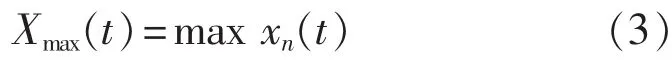
年度数据的标幺化处理：

1.3 求平均值

综合多年数据，对每年的标幺值求平均值：

1.4 修正

多年的平均值得出的结果往往没有标幺值为1的月份或者时刻点，需要对数据进行修正。

式中：k∈（1，2，…，n）

令Ck=1代入公式（7）得：

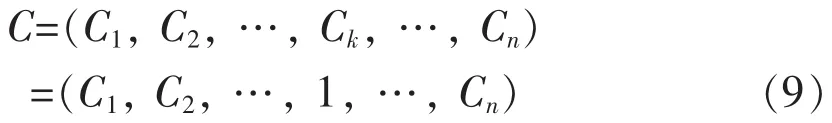
综上，数列C即为以现状数据为基础得出的多年平均年负荷特性曲线，或者多年平均典型日负荷特性曲线。

1.5 负荷特性指标

在多年平均年负荷特性曲线或者多年平均典型日负荷特性曲线的基础上，计算下列负荷特性指标。

（1）典型日的年平均日负荷率γav

在工程实际中，要收集全年8760 h的负荷数据较难实现，因而在典型日24 h负荷数据的基础上计算典型日平均日负荷率，作为年平均日负荷率 γav， 即：

式中： P典型日·av为典型日的日平均负荷； P典型日·max为典型日的日最大负荷。

典型日可以分为丰水期典型日和枯水期典型日，具体划分要在充分了解当地电网多年运行情况和气候等因素的基础上进行。

（2）典型日的年平均日最小负荷率βav

在工程实际中，可用典型日平均日最小负荷率作为年平均日最小负荷率，即：

式中： P典型日·min为典型日的日最小负荷； P典型日·max为典型日的日最大负荷。

（3）年平均月负荷率[1]σav

年平均月负荷率σav又称月不均衡系数，是指1年中各月平均负荷之和与各月最大负荷日平均负荷之和的比值，即：

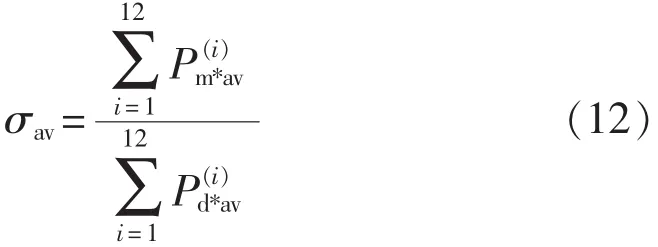
（4）季不平衡率 ρav

季不平衡率ρav又称季不平衡系数，是指1年中各月最大负荷日的最大负荷之和的平均值与年最大负荷的比值，即：

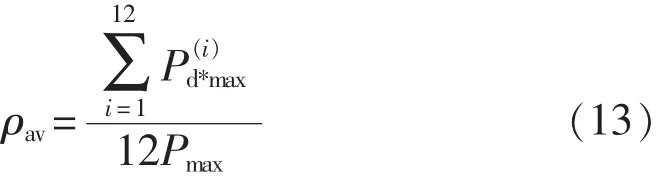
2 负荷特性预测

2.1 年负荷特性

在年负荷特性中，季不平衡率ρav与年负荷曲线的波动性和年最大负荷出现的时间有关，而影响年负荷曲线形状的主要因素是负荷的季节变化、用电设备的大修及负荷在年内的增长。

年负荷特性预测的具体步骤如下：

（1）由历史数据求出历史平均年负荷曲线的季不平衡率ρav。

（2）根据历史数据，用灰色预测法预测未来第 i年的季不平衡率 ρav， 表示为 ρ预测·i。

（3）将以上预测出的 ρ预测·i和历史平均年负荷曲线代入下式，求出预测年各月的负荷标幺值。

式中： Pm·ij为预测第 i年第 j月的负荷标幺值； Pav·j为历史平均年负荷曲线第j月的负荷标幺值。

（4）将预测出的年负荷曲线负荷最大月份的数值修正为1（标幺值），重新计算季不平衡率ρav，并相应计算其他参数。

2.2 日负荷特性

在典型日负荷特性中，年平均日最小负荷率βav与曲线的峰谷差有关，而影响曲线波动峰谷差的主要因素是用电结构比例和气候变化。

日负荷特性预测的具体步骤如下：

（1）由历史数据求出历史平均典型日负荷曲线的最小负荷率βav。

（2）根据历史数据，用灰色预测法预测出未来第i年典型日的最小负荷率βav，冬季和夏季分别表示为 β预测·夏·i（未来第 i年夏季典型日的最小负荷率）、 β预测·冬·i（未来第 i年冬季典型日的最小负荷率）。

（3）将以上预测出的 β预测·夏·i， β预测·冬·i和历史平均典型日负荷曲线代入下式，求出预测年份典型日各时刻的负荷标幺值。

式中：Pt·夏·ij为预测第i年夏季典型日第j时刻的负荷标幺值； Pt·av·夏·j为历史平均夏季典型日负荷曲线第j时刻的负荷标幺值；βav·夏为历史平均夏季典型日负荷曲线的最小负荷率。

式中：Pt·冬·ij为预测第i年冬季典型日第j时刻的负荷标幺值； Pt·av·冬·j为历史平均冬季典型日负荷曲线第j时刻的负荷标幺值；βav·冬为历史平均冬季典型日负荷曲线的最小负荷率。

（4）将预测出的典型日负荷曲线负荷最大时刻的数值修正为1（标幺值），并重新计算最小负荷率βav及相应的其他参数。

3 算法流程

通过以上的分析及数据处理，可以建立相应的算法对现状数据进行分析，并在此基础上对未来几年的负荷特性曲线进行预测，计算结果可用于指导电网年度运行计划的制定。具体算法流程如图1所示。

图1 算法流程

（1）输入数据：输入数据为多年的年负荷特性和日负荷特性数据，这些数据来源于某一地区的供电公司和电网规划报告。

（2）假设条件：用典型日的最小负荷率βav来代替全年的日最小负荷率。

（3）输出数据：输出数据为预测出的年负荷特性曲线和日负荷特性曲线。

4 实际应用

针对某实际系统，收集到相关数据后，利用以上算法得到了预测的年负荷特性曲线和日负荷特性曲线。

4.1 年负荷特性预测

该区域电网年负荷特性预测结果见图2，其中实线、虚线和点划线分别表示现状、2015年和2020年的预测曲线。

图2 年负荷特性

由图2可知：

（1）季不平衡率ρav由现状多年平均的0.861提升到2015年的0.874和2020年的0.877，年负荷曲线的波动稳步减小，符合该地区大力发展第二产业的发展方向。

（2）负荷曲线表明最大负荷出现在12月份，这是由于该地区大型工业在年底赶工和居民取暖用电比例提高，符合该地区的现状。

4.2 夏、冬两季日负荷特性预测

对该区域电网夏、冬两季典型日负荷曲线进行预测，结果表明：

（1）夏季典型日的年平均日负荷率γav由现状的0.872上升到2015年的0.887和2020年的0.890；冬季典型日的年平均日负荷率γav由现状的0.834上升到2015年的0.841和2020年的0.842。表明日负荷曲线的峰谷差减小，这是因为三班制的重工业用电所占比例进一步增加，第三产业和第一产业用电比例略有降低，符合该区域电网的发展趋势。

（2）从夏季和冬季典型日平均负荷区域曲线预测看，在18∶00左右有1个高峰，这是由于三班制重工业的持续生产加上18∶00为居民生活用电高峰，符合该区域电网现状。

5 结语

针对电力负荷特性在实际应用中数据离散性较大的特点，从工程角度出发提出了一种新的负荷特性分析预测方法。采用具有代表性的典型数据并对其进行标幺化和修正处理，强化了数据的一致性，然后计算负荷特性的相关指标，进而对年负荷特性和日负荷特性进行预测。简化了负荷特性预测算法，提高了算法的可操作性，克服了传统算法数据需求量大的不足，准确度较高，能够反映负荷特性的变化规律，可用于电网发展基本成型的城市和地区的负荷特性分析预测，对电网规划及电力调度等具有一定的参考价值。

通过对某实际电网具体数据进行的测算，证明了该算法的适应性，预测结果符合该地区的现状和发展趋势。该算法已经应用于该地区的电网规划工作，为该地区的负荷特性分析提供了有力的支撑。

[1] 赵希正，周小谦，姜绍俊.中国电力负荷特性分析与预测[M].北京∶中国电力出版社，2002.

[2] 陈健，刘明波，樊亚亮.广州电网负荷特性分析[J].电力系统及其自动化学报，2009，21（6）∶78-83.

[3] 叶刚健，蒋金良.汕头电网负荷特性分析与预测[J].电力系统及其自动化学报，2004，16（6）∶55-59.

[4] 李鹏，任震.广州电网负荷特性分析及短期预测模型设计[J].电力自动化设备，2002，22（8）∶50-53.

[5] 赵永良，易武，谢开贵.固原电网负荷特性分析[J].电网技术，2007，31（2）∶230-232.

[6] 姜勇.南京市居民夏季用电负荷特性分析[J].继电器，2003，31（4）∶24-26.

[7] 徐方龙，谢国栋，黄苏融，等.上海市区供电局电力负荷特性分析[J].上海大学学报（自然科学版），2000，6（3）∶222-226.

[8] 杨宗麟.华东电网负荷特性分析预测[J].华东电力，2008，36（5）∶50-52.

[9] 陈健.广州电网负荷特性研究[D].华南理工大学电力学院，2007.

[10] 姜勇.南京地区春节负荷特性分析及其预测方法[J].电网技术，2003，27（5）∶72-74.