K空间抽样格林函数在正向重构时的误差分析

唐 波, 苑秉成, 徐 瑜



K空间抽样格林函数在正向重构时的误差分析

唐 波, 苑秉成, 徐 瑜

(海军工程大学, 兵器工程系, 武汉 湖北, 430033)

在近场声全息重构过程中, 当采用K空间抽样格林函数进行大距离正向重构时, 会产生极大的误差, 而传统的加窗处理不能有效抑制这种误差的产生。文中在分析了误差是K空间抽样格林函数幅值突变而产生的频谱泄露和边缘吉布斯效应的基础上, 提出了有针对性的改变窗函数的截止波数, 使格林函数幅值突变部位得到有效平滑, 进而抑制这种误差产生的方法。仿真结果表明, 经改进的窗函数能够对K空间抽样格林函数大距离正向重构时的误差起到明显的抑制作用, 使此条件下的全息重构具有更加良好的效果。

近场声全息; K空间; 格林函数; 正向重构; 窗函数

0 引言

近场声全息技术是上世纪80年代从全息领域脱颖而出的新技术。它借助重构面与全息面之间的空间场变换关系, 由全息面声场变换得到重构面声场。近场声全息技术特别适用于低频场源特性判别、散射体结构表面特性以及结构模态振动等研究。

平面近场声全息技术是全息面和重构面均为平面的正交共形近场声全息技术。在平面近场声全息技术中, 当采用K空间抽样格林函数进行正向重构时, 重构结果对重构距离极为敏感, 当重构距离很小时, 重构具有很高的精度。而当重构距离较大时, 重构误差急剧增加[1]。目前的研究认为，这种误差来源于采用K空间抽样格林函数进行重构时的卷绕误差, 并且这种情况下, 对格林函数加窗不能对误差的减少产生明显作用。

1 K空间抽样格林函数特性分析

由近场平面声全息基本理论可知, 正向重构时K空间抽样格林函数的数学表达式为

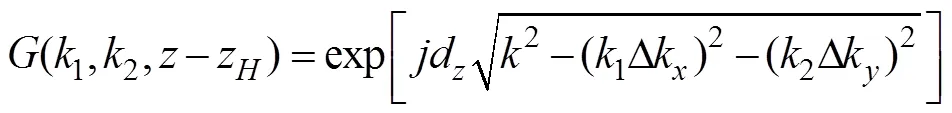
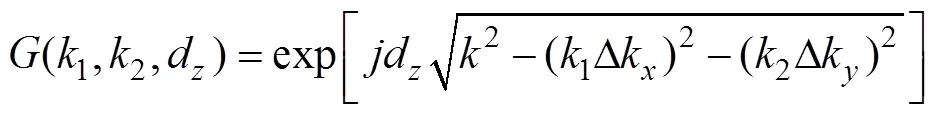
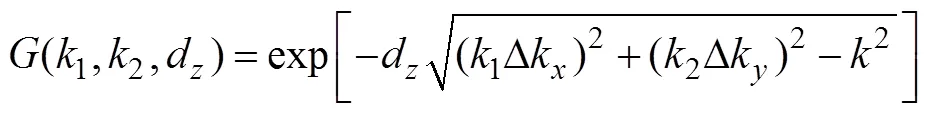
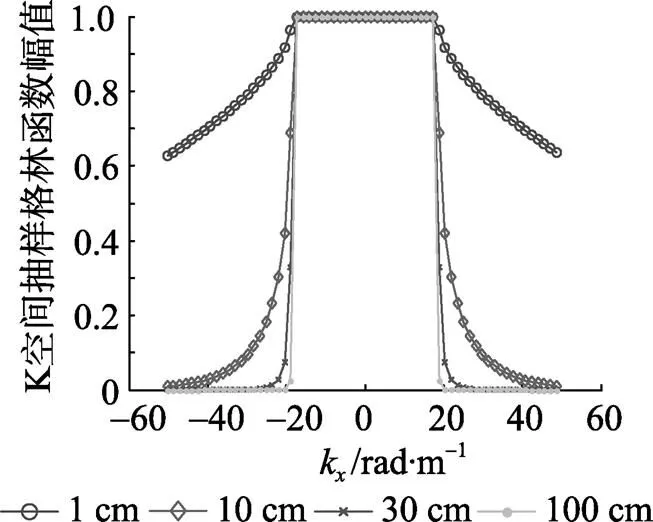
图1 不同重构距离时的K空间格林函数分布图

由图1可以看出, 随着重构距离的增大, 位于辐射圆之外的格林函数幅值衰减越来越厉害。当重构距离达到100 cm时, 辐射圆之外的格林函数迅速减小至零, 这将导致在辐射圆附近K空间抽样格林函数产生突变, 这种突变会产生类似数据截断的效应, 在逆傅氏变换时将在实空间域导致重构信号的剧烈波动, 产生极大的重构误差。

2 加窗处理

由以上分析可以看出, 当采用K空间抽样格林函数进行全息重构时会产生误差。为了抑制重构过程带来的误差, 需要采用一定的滤波措施, 全息重构中常采用加窗函数来减小误差。

在各种滤波窗函数中, 文献[5]提出的窗函数应用最广泛, 该函数通过在截止波数处采用平滑处理, 获得了很好的滤波效果。该窗函数的表达式为

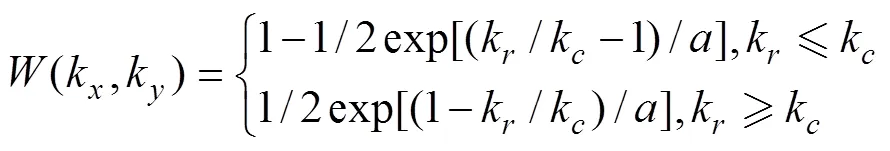
在该函数中截止波数的选择非常重要, 对滤波的结果影响非常大。目前在正向重构过程中, 对K空间抽样格林函数进行加窗处理时, 选择截止波数仍然采用经验公式

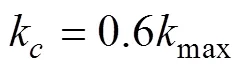
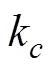
“这是你祖姑婆给你的，对吗？”乌有先生接过玉玦，沉沉生碧，月光里柔美温润，带着女孩的体温。女孩幽兰一般的气息，白玉般略宽的脸庞，灵慧的眼神，热烈而坚定，何其熟悉。今夜星雪海，似是故人来。他想起一个甲子之前的长安，乌有也是鲜衣怒马的少年郎，整天魂牵梦绕，想念深宫里明眸善睐的佳人，他满世界去抄龙族、鬼母的传奇送她看，她则托人将冰雪深沃的交州荔枝带出来给他吃，将新写的诗给他念。

由图2可以清晰地看出, 因为较小重构距离下格林函数在孔径内没有得到充分的衰减, 从而在孔径边缘处由于截断产生了幅值突变, 同时在辐射圆附近没有幅值突变(如图1中重构距离1 cm的曲线), 因此以往的加窗处理是有效的(如图2中重构距离1 cm的曲线)。

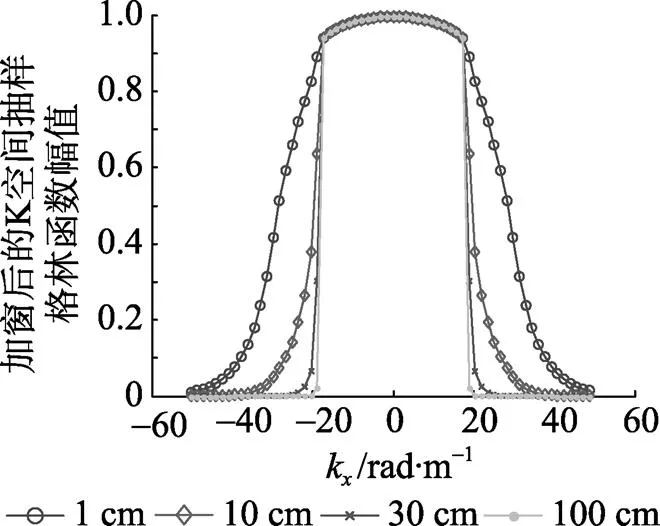
图2 加窗后的K空间抽样格林函数分布图

然而在大距离重构条件下, 格林函数在孔径内已经得到充分衰减, 因此在孔径边缘处不存在幅值突变, 而在辐射圆附近却存在幅值突变, 迅速从1变化为0(如图1中重构距离100 cm的曲线), 因此用于平滑孔径边缘处函数值的窗函数无法平滑辐射圆附近的幅值突变(如图2中重构距离100 cm的曲线), 从而无法抑制这种突变引起的吉布斯效应, 也就无法减小重构误差。

基于以上分析讨论, 需要有针对性的改变窗函数的结构, 使窗函数能够对辐射圆附近的幅值突变产生平滑作用。本文通过改变截止波数的方法来实现。

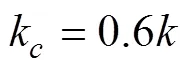
此时对于窗函数表达式(4)来说, 截止波数的改变意味着窗孔尺寸的改变, 如图3所示。

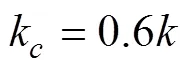
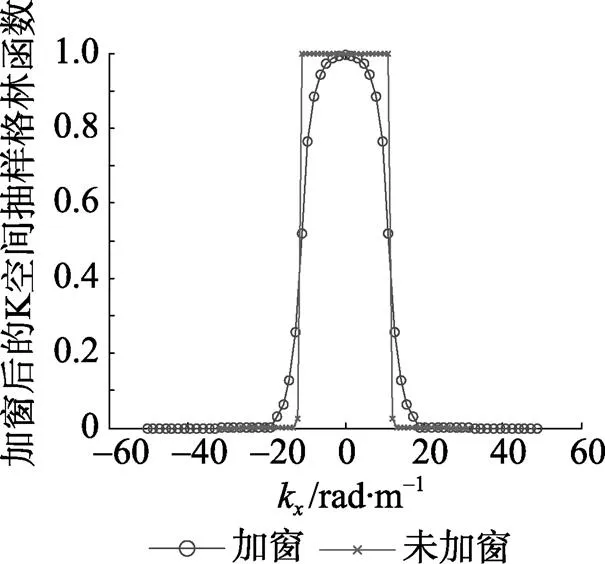
图4 加改进窗的K空间抽样格林函数分布图

图4可清楚看到, 改进的窗函数对格林函数在辐射圆附近的幅值突变起到很好的平滑作用。

3 仿真验证

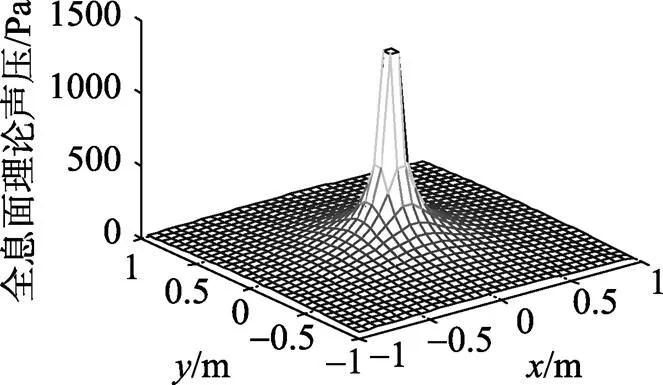
图5 全息面理论声压幅值

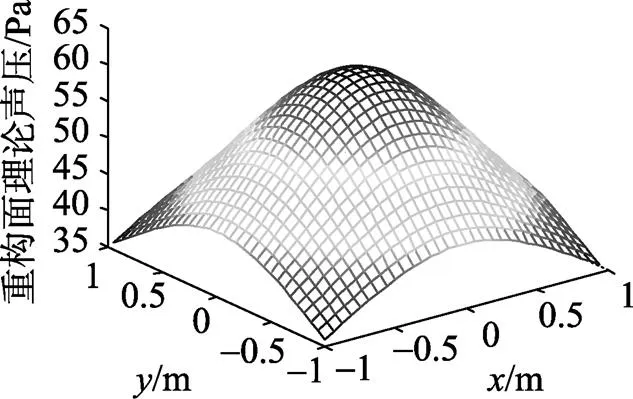
图6 重构面理论声压幅值

不加窗时的重构结果如图7所示。

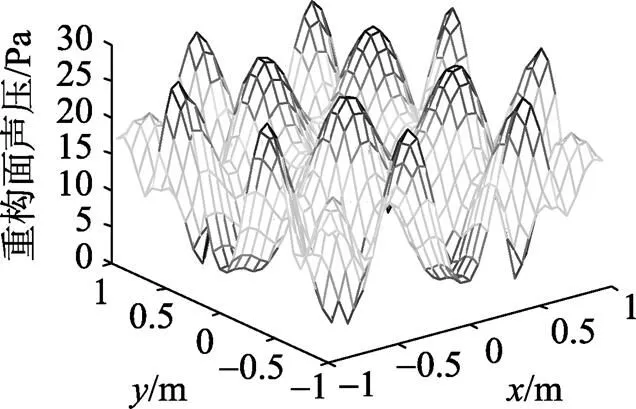
图7 不加窗时重构面声压幅值

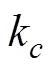
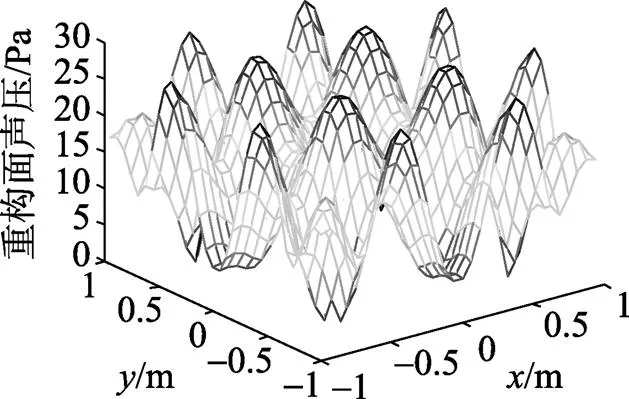
图8 加窗时重构面声压幅值

由图7和图8可以看出, 不加窗和加采用式(5)截止波数的窗函数, 其重构结果没有明显的改变, 因此加采用式(5)截止波数的窗函数不能有效地抑制K空间抽样格林函数大距离正向重构时的重构误差。

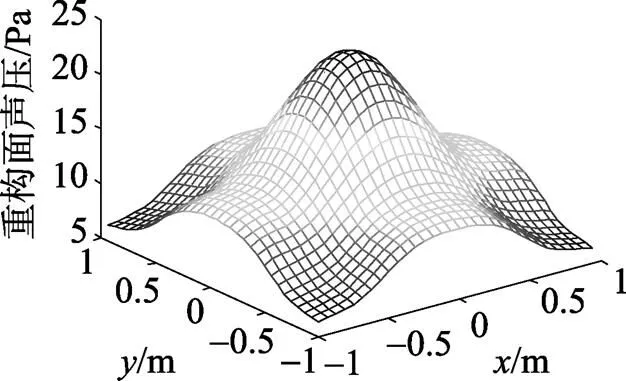
图9 加改进窗时重构面声压幅值

由图9可以看出, 改进的窗函数可以有效地抑制K空间抽样格林函数大距离正向重构时的重构误差。

7和图8可以看出，相对误差超过了100%，完全淹没了声压信息。同时，在对信号进行加窗和滤波处理时，在抑制误差干扰时，也会对信号有一定程度的削弱，致使重构幅度变小，对比图6和图9可以清晰的看到这点，虽然重建声压值降到了理论声压值一半左右，但相对误差减小到了10%左右，能够真实反映重构面的声压信息。

4 结束语

从以上的理论推导和仿真验证可以看出, 当采用K空间抽样格林函数进行大距离正向重构时, 由于格林函数位于辐射圆内低波数成分幅值恒为1, 而位于辐射圆之外的高波数成分几乎衰减至零[9], 以至在辐射圆附近格林函数幅值发生突变, 这种突变会产生类似数据截断的效应, 在全息重构中产生极大的误差。

传统的加窗处理只是用窗函数来平滑孔径边缘处的函数值, 无法消除辐射圆附近的格林函数幅值突变, 也就无法抑制这种幅值突变给全息重构带来的误差, 因此无法有效地改变全息重构的效果。

改进的窗函数针对格林函数幅值发生突变的位置, 改变窗孔大小, 能够有效的平滑处理辐射圆附近的格林函数幅值突变, 也就抑制了这种突变带来的误差效应, 使重构结果符合声场实际分布。仿真结果表明, 该改进的窗函数能够对K空间抽样格林函数大距离正向重构时的误差起到明显的抑制作用, 使此条件下的全息重构具有更加良好的效果。

[1] 何琳. 声学理论与工程应用[M]. 北京: 科学出版社, 2006: 374-375.

[2] 辛雨. 基于空间声场变换的近场声全息参数选取及重建误差研究[D]. 合肥: 合肥工业大学, 2009: 64-66. Xin Yu. Research on Selection of Parameters and Recon- struction Error in the NAH based on STSF[D]. Hefei: Hefei University of Technology，2009: 64-66.

[3] 郑旭. 平面近场声全息在噪声源识别中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2008: 75-86. Zheng Xu. The Application of Planar Near-field Acoustical Holographic in Noise Source Identification[D]. Harbin: Har- bin Engineering University, 2008: 75-86.

[4] 邓江华, 刘献栋, 单颖春, 等. 声场中倏逝波特性及改进全息重建方法的研究[J]. 噪声与振动控制, 2009(4): 168-172. Deng Jiang-hua, Liu Xian-dong, Shan Ying-chun, et al. Study on Characteristics of Evanescent Wave in Acoustic Field and Improvement of Holography Reconstruction Method[J]. Noi- se and Vibration Control, 2009(4): 168-172.

[5] Veronesi W A, Maynard J D. Near-field Acoustic Holography (NAH): Holographic Reconstruction Algorithms and Compu- ter Implemention[J]. The Journal of the Acoustical Society of America, 1987, 81(5): 1307-1322.

[6] 薛玮飞. 机械噪声源辨识与特征提取的研究[D]. 上海: 上海交通大学, 2007: 42-43.

Xue Wei-fei. Research on Mechanical Noise Sources Iden- tification and Feature Extraction[D]. Shanghai: Shanghai Jiao Tong University, 2007: 42-43.

[7] 于飞, 陈剑, 周广林, 等. 噪声源识别的近场声全息方法和数值仿真分析[J]. 振动工程学报, 2003, 16(3): 339-343. Yu Fei, Chen Jian, Zhou Guang-lin, et al. A Study on Noise Sources Identification Using Near Field Acoustic Holography Method and Its Numerical Simulation Analysis[J]. Journal of Vibration Engineering, 2003, 16(3): 339-343.

[8] 陈晓东. 近场平面声全息的测量和重构误差研究[D]. 合肥: 合肥工业大学, 2004: 57-59. Chen Xiao-dong. Research on the Measurement and Recon- struction Error in the NAH[D]. Hefei: Hefei University of Technology, 2004: 57-59.

[9] Maynard J D, Williams E G, Lee Y. Near-field Acoustic Holo- graphy Ⅰ: Theory of Generalized Holography and the Development of NAH[J]. The Journal of the Acoustical Soci- ety of America, 1985, 78(4): 1395-1412.

Error Analysis of Green′s Function Sampled in K-space for Forward Reconstruction

TANG Bo, YUAN Bing-cheng, XU Yu

(Department of weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

During the near-field acoustic holographic reconstruction, tremendous errors will appear when using Green′s function sampled in K-space for long distance forward reconstruction, and conventional window function cannot restrain the error efficiently. In this paper, the error is analyzed to be generated by spectrum leakage and edge Gibbs phenomenon derived from amplitude discontinuity of Green′s function sampled in K-space, hence a corresponding method for changing the cut-off wave number of window function is represented to smooth the amplitude discontinuity and further to restrain the error. Simulation result shows that the improved window function can obviously reduce the error in the holographic aperture, and the present method is efficient in restraining the error generated by spectrum leakage and Gibbs phenomenon derived from amplitude discontinuity of Green′s function sampled in K-space.

near-field acoustic holography; K-space; Green′s function; forward reconstruction; window function

TJ630; TB525

A

1673-1948(2012)02-0095-05

2011-08-27;

2011-09-29.

唐 波(1980-), 男, 在读博士, 主要研究方向为制导与控制技术.

(责任编辑: 杨力军)