一种加权对称损失函数下Rayleigh分布尺度参数倒数的Bayes估计

任亮，褚衍彪，2

(中国矿业大学 理学院，江苏 徐州 221116； 枣庄学院 数学与统计学院，山东 枣庄 277160)

0 引言

Rayleigh分布 R(x,σ)是很重要的寿命分布，它主要用来描述零件，构件承受非稳定循环力时应力幅的分布规律，也用于描述平坦衰落信号接收包络或独立多径分量接收包络统计时变特性的一种分布类型.两个正交高斯噪音信号之和的包络服从瑞利分布，它是为威布尔分布W(μ,α,β)的重要成员，其密度函数为

定义1.1[1]设Χ是随机变量，如果Χ的分布密度为

(1)

则称随机变量Χ服从Rayleigh分布.其中σ>0为尺度参数.设随机变量Χ服从Rayleigh，Χ1,Χ2......Χn来自总体Χ的容量为n的简单随机样本，则其联合概率密度为

(2)

(3)

目前，关于Rayleigh分布的Bayes估计的文章并不少.如林金官在文献[2]中介绍了Rayleigh分布参数的几种估计；Chung Younshik在文献[3]中给出了尺度参数和尺度参数平方的几种估计；邱燕等在文献[1]给出了熵损失下Rayleigh分布尺度参数倒数的Bayes估计,徐宝等在文献[4]给出了一种加权对称损失函数下一类指数分布模型参数的估计.本文讨论在加权对称损失函数下对θ讨论Bayes估计和容许性.

1 加权对称损失下的Bayes估计

我们定义加权p,q对称熵损失函数[4]

(4)

在这里υ是n的函数，n是样本容量.

定理1.1 在损失函数(4)下，对于任意的先验分布，参数θ的Bayes估计为

( 5)

证明见文献[4].

接下来，我们讨论θ在三种常见先验情形下的Bayes估计的精确形式.

首先，θ的先验分布π(θ)服从Bayes假设，令θ服从U(0,c),c为已知常数且c>0，则

(6)

(7)

证明：取(6)为θ的先验分布，得到θ的后验密度函数为

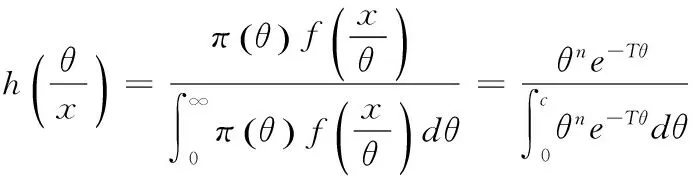
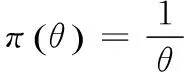
(8)

则Bayes估计为

(9)

证明：后验密度为

则Bayes估计为

在上述情况下，δB3中仍然含有超参数α,λ，因此需要进一步讨论θ的多层Bayes估计.根据多层先验分布的构造方法以及Rayleigh分布的特征，选取减函数法[5]构造θ的先验分布

(10)

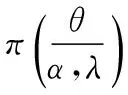
π*(α)=U(0,1),

(11)

π*(λ)=U(0,c),

(12)

c为常数

定理1.5 对于Rayleigh分布，取(12),(13)为θ的先验分布，在损失函数(4 )下,θ的Bayes估计为

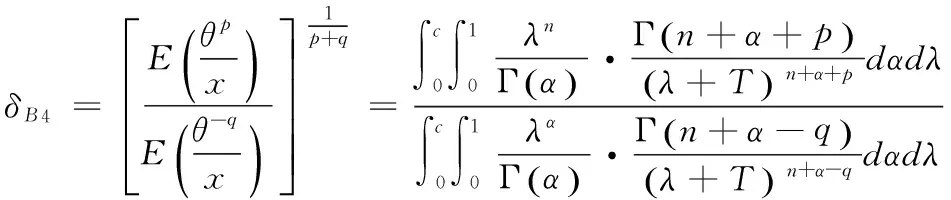
(13)

证明：由定理1.1可得

2 容许性

引理2.1[6]在给定的Bayes决策问题中，假如对给定的先验分布π(θ)的Bayes估计δB是唯一的，则它是可容许的.

定理2.2 对于Rayleigh分布，取Γ(α,λ)为θ的先验分布，在损失函数 (3)下，θ的Bayes估计是可容许的.

事实上，由于加权对称损失函数是关于δ严格凸的，其Bayes估计是唯一的，于是由引理2.1即得定理.

参考文献

[1]方开泰，徐建伦.统计分析[M]. 北京：科学出版社，1987.

[2]林金官.Parameter Estimations of Rayleigh Distribution[J].数学季刊，2000,15(4)：49-54.

[3]ZHANG Min-Yue,ZHANG Li Yuang. Application of inverse Gaussion distribution in mathematical of realiability[J].兰州大学学报(自然科学版)，2003,39(3)：23-24.

[4]徐宝，姜玉秋，滕飞.一种加权对称损失函数下一类指数分布模型参数的估计[J].四川师范大学学报(自然科学版)，2011,34(4)：484-4867.

[5]韩明.多层先验分布的构造及应用[J].运筹与管理，1997,6(3)：31-40.

[6]茆诗松，王静龙，濮晓龙.高等数理统计[M].北京：高等教育出版社，1998.