时标上具有依赖状态脉冲动力系统的实用稳定性
张忠军, 陈雁东,2, 杨 军,3
(1.燕山大学 理学院 河北 秦皇岛 066004;2.广灵县第一中学校 山西 大同 037500; 3.河北省数学研究中心 河北 石家庄 050000)
0 引言
由于时标上动态系统的理论能将连续和离散理论很好统一起来,已得到了广泛关注,也取得了一些成果[1-2],但对时标上脉冲动力系统的实用稳定性的研究还非常少见[3].关于时标上具有依赖状态的脉冲动力系统的实用稳定性至今还没有相关文献.本文在文献[4-6]的基础上,考虑时标上具有依赖状态脉冲的动力系统关于两个测度的实用稳定性,将测度函数与Lyapunov函数的特征结合起来,直接利用两个测度函数h0和h本身的特性,仅对两个测度函数中的一个适当加条件,而无需另外构造Lyapunov函数,就得到了判定(h0,h)-实用稳定性的充分条件.
1 预备知识
考虑具有依赖状态脉冲动力系统
(1)
其中,T为时标(具有标准顺序和拓扑结构的实数R的任意非空闭子集),xΔ(t)表示x(t)在t处的Δ导数,且满足下列条件:
(i)f∈CrdT×Rn,Rn,在τk,τk+1上右稠密连续,且
(iii)Ik∈CrdRn,Rn,k=1,2,…,且(1)式的任意解撞击给定的脉冲面Sk:t=τk(x)仅一次;
(iv)f(t,0)≡0,Ik(0)=0.

为以后叙述方便,假定τ0(x)≡t0,且给出如下记号:
K={u∈Crd[R+,R+]:u(0)=0且u严格单调递增},
CK={u∈Crd[T×R+,R+],∀t∈T,u(t,·)∈K},
Γ= {h:Crd[T×Rn,R+],h在所有集合Gk上连续且对
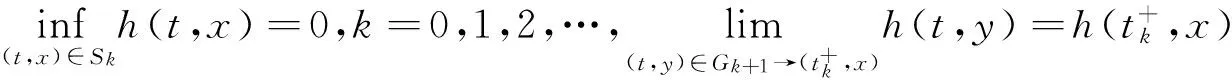
S(h,ρ)={(t,x)∈T×Rn:h(t,x)<ρ,ρ>0,h∈Γ}.
定义1设h0,h∈Γ,称脉冲动力系统(1)为
(i)(h0,h)-实用稳定,如果给定(λ,A),0<λ h(t,x(t)) (ii)(h0,h)-一致实用稳定,如果对所有t0∈T,(i)都成立. 定义2设h∈Γ,(t,x)∈G0,定义 易知,若h(t,x)关于x满足局部Lipschitz条件,当T=R时,有 其中,x(t)=x(t,t0,x0)为脉冲动力系统(1)的任意解. 定理1假设 (i)h0,h∈Γ,且存在0<λ h(t,x)≤φ(t,h0(t,x)),(t,x)∈T×S(h0,λ0); (ii)当(t,x)∈G0时,h(t,x)关于x满足局部Lipschitz条件,且 D+hΔ(t,x)≤0,(t,x)∈G∩S(h0,ρ); (iii)h(t+0,x+Ik(x))≤h(t,x),(t,x)∈Sk∩S(h,ρ); (iv)存在ρ0∈(0,ρ)使得当(t,x)∈Sk∩S(h,ρ0)时有h(t+0,x+Ik(x))≤ρ,则脉冲动力系统(1)为(h0,h)-实用稳定的. 证明任给A∈(0,ρ),t0∈T,由φ∈CK知存在λ∈(0,λ0)使得φ(t0,λ) h(t0,x0)<φ(t0,h0(t0,x0))≤φ(t0,λ) 下证对系统(1)的满足h0(t0,x0)<λ的任意解x(t)有 h(t,x(t)) (2) h(t*,x(t*))≥A且h(t,x(t)) A≤h(t0,x(t0))<ρ且h(t,x(t))<ρ,t∈[t0,t0]. 因此由条件(ii)和条件(iii)知,t∈[t0,t0]时h(t0,x(t))为非增的,故 h(t,x(t))≤h(t0,x0),t∈[t0,t0]. 因此有h(t0,x(t0))≤h(t0,x0) 定理2在定理1的基础上,将条件(i)加强为 (i*)h0,h∈Γ,且存在λ0>0,φ∈K,使得 h(t,x)≤φ(h0(t,x)),(t,x)∈S(h0,λ0), 则脉冲动力系统(1)为(h0,h)-一致实用稳定的. 证明任意A∈(0,ρ0),t0∈T,由φ∈K知存在λ∈(0,λ0),使得φ(λ) 参考文献: [1] Hilger S. Analysis on measure chains: a unified approach to continuous and discrete calculus[J]. Res Math, 1990,18(1):18-56. [2] Agarwal R P, Bohner M, Oregan D, et al. Dynamic equation on time scales: a survery[J]. Comput Appl Math, 2002, 141(1/2): 1-26. [3] 武萌,赵新生,贾培佩.时间尺度上脉冲动力系统的实用稳定性[J].数学的实践与认识,2007, 37(19):1-3. [4] 杜静,傅希林.时标上非线性脉冲动态系统的稳定性[J].山东师范大学学报:自然科学版, 2007,23(1):1-3. [5] Wang Peiguang, Liu Xia.Practical stability of impulsive hybrid differential systems in terms of two measures on time scales[J].Nonlinear Analysis,2006,65(11):2035-2042. [6] Wang Peiguang,Liu Xia. New comparison principle and stability criteria for impulsive hybrid systems on time scales[J].Nonlinear Analysis: Real World Application,2006,7(5): 1096-1103.2 主要结果



