Computationally Efficient Nonlinearity Compensation for Coherent Fiber-Optic Systems

Likai Zhu and Guifang Li

(CREOL,The College of Optics and Photonics,University of Central Florida,4000 Central Florida Boulevard,Orlando,Florida 32816,USA)

Abstract Split-step digital backward propagation(DBP)can be combined with coherent detection to compensate for fiber nonlinear impairments.A large number of DBPsteps is usually needed for a long-haul fiber system,and this creates a heavy computational load.In a trade-off between complexity and performance,interchannel nonlinearity can be disregarded in order to simplify the DBPalgorithm.The number of steps can also be reduced at the expense of performance.In periodic dispersion-managed long-haul transmission systems,optical waveform distortion is dominated by chromatic dispersion.As a result,the nonlinearity of the optical signal repeats in every dispersion period.Because of this periodic behavior,DBPof many fiber spans can be folded into one span.Using this distance-folded DBPmethod,the required computation for a transoceanic transmission system with full inline dispersion compensation can be reduced by up to two orders of magnitude with negligible penalty.The folded DBPmethod can be modified to compensate for nonlinearity in fiber links with non-zero residual dispersion per span.

Keyw ords coherent fiber communication;nonlinearity compensation;folded digital backward propagation

1 Introduction

C oherent detection is emerging as the most attractive candidate for next-generation fiber communication systems.A coherent detector is highly sensitive and can detect all the information about the optical field,including amplitude,phase,and polarization.This enables linear and nonlinear impairments to be compensated for using digital signal processing(DSP).

Chromatic dispersion is usually a dominant factor that distorts the optical waveform as it propagates along the fiber.In most fiber links,chromatic dispersion is optically compensated for by cascading two or more kinds of fiber with inverse dispersion parameters.New inverse dispersion fibers compensate for both dispersion and dispersion slope while minimizing the total polarization mode dispersion(PMD).This results in wideband dispersion flatness[1].With coherent detection,chromatic dispersion and PMD can also be compensated for using DSP[2].

Nonlinear impairments,including self-phase modulation(SPM),cross-phase modulation(XPM)and four-wave mixing(FWM),increase with launching power.Atrade-off between high optical signal-to-noise ratio(OSNR)and low nonlinear impairments results in a power level that allows optimal performance in a fiber link.As linear impairment compensation technology matures,nonlinear effects become the factor that limits the capacity and transmission distance of long-haulfiber communication systems[3].

Opticalpropagation in fiber is governed by the nonlinear Schröd inger equation(NLSE),which has no analytical solution.Thus,split-step digital backward propagation(DBP)is necessary to compensate for the joint effects of dispersion and nonlinearity.For the split-step method to be accurate,the step size has to be small enough for the linear and nonlinear effects to be decoupled in each step;however,this results in heavy computational load[4],[5].

2 Simplified DBP Methods

In[6],DSPfor wavelength-division multiplexing(WDM)transmission was performed by solving the NLSEfor the total opticalfield in the fiber.With phase-locked local oscillators,the relative phases between the WDM channels are preserved so that the total optical field can be reconstructed before DBP.The SPM,XPM,and FWM can be compensated for using the total-field NLSE;however,the large totalopticalbandwidth results in a small dispersion-limiting step size and high sampling rate[7].

DBPcan also be performed by disregarding the FWM and solving the coupled NLSE.Compared to solving the total-field NLSE,solving the coupled NLSErequires a smaller step number and lower sampling rate[8],[9].In addition,phase-locking between the local oscillators is not necessary.In the coupled NLSEalgorithm,the step number can be further reduced by factorizing the dispersive interchannel walk-off effects[10].

Moreover,compared to interchannel nonlinearity compensation,intrachannelnonlinearity compensation usually requires a smaller number of steps because the step size is not limited by the interchannel walk-off effect.In[11]and[12],Fujitsu gave the results of one-step-per-span DBP for intrachannel nonlinearity compensation of dual polarization quadrature phase-shift keying(DP-QPSK)transmission.

As a one-step-per-link approach,lumped-phase de-rotation is proportional to the received single-channel optical intensity and can be used for SPM compensation[13],or it is proportional to the multichannel optical intensity and can be used for XPM compensation[14].The lumped-phase de-rotation method is based on the assumption that the intensity waveform remains unchanged throughout the fiber propagation.

In the split-step DBP,the step size has to be small enough so that the linear dispersion and nonlinear effects being compensated for are accurately described.Because the optical intensity along the fiber varies,step sizes can be variable to minimize the number of steps[5].The DBP algorithm can be simplified by neglecting FWM or XPM;however,for a fiber link in which chromatic dispersion causes significant pulse reshaping and interchannel walk-off,multiple steps per span are usually needed,especially for interchannel nonlinearity compensation.Reducing complexity by simply increasing the step size reduces performance.

In addition to these DBPmethods,other DSPmethods combined with coherent detection have been proposed for nonlinearity compensation.In[15],adaptive filtering in carrier phase recovery(AFCPR)was proposed to suppress nonlinear phase noise.However,information about the neighboring channels,which is necessary for complete XPM compensation,is not used in the AFCPRalgorithm.In[16],a pilot-based XPM compensation method for a coherent optical(CO-OFDM)system is proposed.This method may not be applicable to systems with other modulation formats.

3 Distance-Folded DBP

In[17],we took advantage of the periodic behavior of an optical signal in a periodic dispersion-managed fiber-optic system to propose a computationally efficient distance-folded DBPmethod for nonlinearity compensation.With periodic dispersion management,the linear and nonlinear behavior of the signal repeats itself in every dispersion period,and the DBPof many fiber spans can be folded into one span.

For long-haul fiber-optic transmission,an optimum power is derived from the trade-off between high OSNRand low nonlinear effects.The nonlinear phase shift at the optimum power level is on the order of one radian[18].Therefore,for transoceanic fiber transmission systems,which consist of more than 100 amplified spans,the nonlinear effects in each span are weak.As a result,chromatic dispersion is the dominant factor that determines the optical waveform evolution within each span.

Assuming weak nonlinearity and periodic dispersion management,the optical field after K spans of propagation is equivalent to the optical field after propagation in one fiber span where the nonlinearity is K times that of the originalfiber.This equivalence suggests that the DBPfor K spans can be folded into a single span with K times the nonlinearity.

Assuming the step size for the split-step implementation of DBPis unchanged,the computational load for the folded DBP can be saved by a folding factor of K.

The assumption that the nonlinear behavior is repeated in every span is not exactly valid because fiber nonlinearity also changes the waveform,and dispersion is not perfectly periodic if the residual dispersion per span(RDPS)is non-zero or if the dispersion slope is not compensated for.These effects accumulate and,as a result,waveform evolutions are not identical between two spans that are far away from each other.In order for nonlinearity compensation to be accurate,the entire long-haul transmission system can be divided into segments of multiple dispersion-managed spans,and distance-folded DBPcan be performed within each segment.For a fiber link with M×K spans,the distance-folded DBPis as in Fig.1.

To demonstrate the effectiveness of the distance-folded DBP,we simulate a WDM system with QPSK modulation at 56 Gbit/s using VPITransmission Maker.The simulation setup is shown in Fig.2.Twelve channels of non-return-to-zero(NRZ)QPSK signal are transmitted with 50 GHz channel spacing.The linewidth of the lasers is 100 KHz.

The dispersion-managed fiber link consists of 140 spans of 50 km of the OFSUltraWave SLA/IDFOcean Fiber combination.The erbium-doped fiber amplifier(EDFA)noise is 4.5 d B.The loss,dispersion,relative dispersion slope,and effective area of the SLAfiber are 0.188 d B/km,19.5 ps/nm/km,0.003/nm,and 106μm2.The corresponding parameters for the IDFfiber are 0.23 d B/km,-44 ps/nm/km,0.003/nm,and 31μm2.A piece of fiber at the receiver was used to compensate for the accumulated residualdispersion.

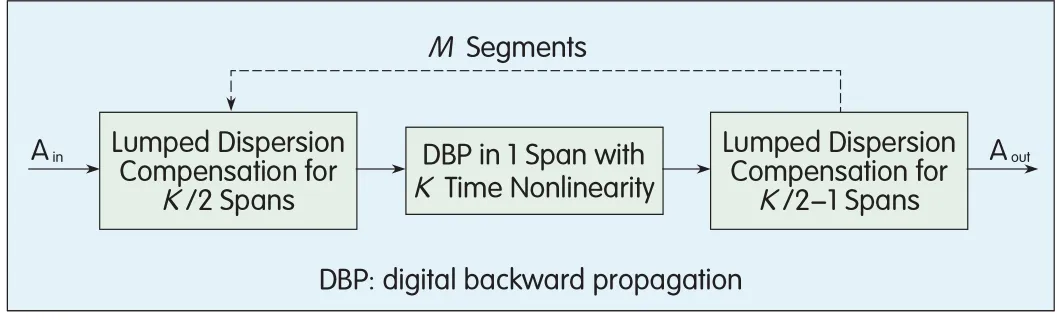
▲Figure 1.Folded DBPfor a periodic dispersion-managed fiber link with M×K spans.

▲Figure 2.Dispersion managed WDMsystem.

The DBPin Fig.1 was performed in Matlab.Without loss of generality,we solved the coupled NLSEwith the non-iterative asymmetric split-step Fourier method(SSFM).In long-haul WDM fiber links,the step size is usually limited by dispersion[4].Therefore,for both SLA fiber and IDFfiber,we used the same number of steps in each span so that the dispersion in each step was approximately the same.After matched filtering,phase estimation,and clock recovery,the Q-value averages of the WDM channels were estimated.

We first simulated the transmission with RDPS=0.The Q-value as a function of the launching power is shown in Fig.3(a).Without nonlinearity compensation,the maximum Q-value was 10.8 d B.With conventional DBPin all spans,the Q-value increased to 13.3 d Bas a result of nonlinearity compensation.With folded DBPthat has a folding factor of 140(M=1,K=140),the maximum Q-value was 13.1 d B.

The 0.2 d B Q-value penalty was due to the accumulated nonlinear waveform distortion,which reduced the accuracy of nonlinearity compensation.There was almost no penalty when the folding factor was 70(M=2,K=70).Fig.3(b)shows the Q-value as a function of step number per span.The folded DBPmethod does not require an increased step number per span.

The nonlinear impairments in a dispersion-managed fiber link can be suppressed with inline residual dispersion[19]-[21].However,the non-zero RDPScan induce a penalty in the folded DBP.Fig.4(a)shows Q-value obtained at the optimum power level as a function of the folding factor K.With an RDPSof 5 ps/nm(20 ps/nm),the maximum Q-value can be approached using a folding factor of 20(5).Fig.4(b)shows Q-value as functions of RDPS.With conventional DBPin all spans,the Q-value increases with RDPSand approaches the maximum value when RDPSis greater than 10 ps/nm.When folded DBPis used,the Q-value penalty increases with RDPS.

▲Figure 3.(a)Q-value vs.launching power per channeland(b)Q-value at optimum power vs.step number per span with RDPS=0 ps/nm.

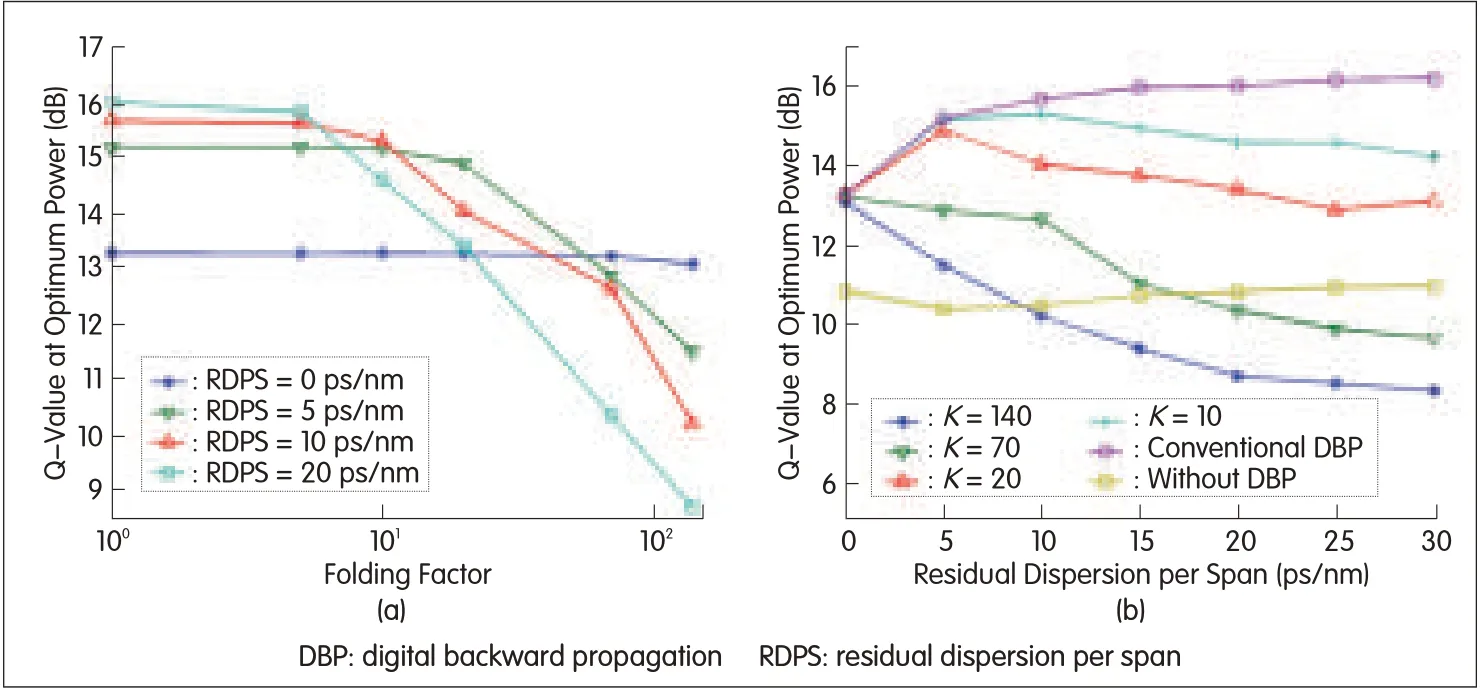
▲Figure 4.(a)Q-value vs.folding factor K and(b)Q-value vs.RDPS.

4 Discussion

In this paper,we have presented a distance-folded DBPmethod for periodic-dispersion-managed fiber systems.Distance-folded DBP minimizes performance penalty for a fiber link with full inline dispersion compensation.However,most of the deployed fiber links have non-zero RDPSin order to avoid resonant nonlinearity.For such fiber links,the computational load required to approach the maximum Q-value increases with the RDPS.

To solve this problem,we have recently used a dispersion-folded DBPmethod instead of a distance-folded DBPmethod.In long-haul fiber transmission,the opticalwaveform and,consequently,the nonlinear behavior of the optical signal repeat at locations of identical accumulative dispersion.Hence,the DBPsteps can be folded according to the accumulated dispersion.The effectiveness of dispersion-folded DBPfor fiber links with large RDPShas been demonstrated numerically and experimentally.