高考数学创新试题之“寻”规“导”矩

陈 昇

高考数学创新试题之“寻”规“导”矩

陈 昇

福建省福州第三中学

该文从创新试题的分布、试题创新点的设置等方面对2012年七省高考数学创新试题深入分析，以此反思实际教学得失，并有针对性地为今后备考高考数学创新试题提出若干建议。

高考数学 创新 试题分析

《普通高中数学课程标准》明确指出“要为学生形成积极主动的、多样的学习方式，进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯”。换而言之，数学课程的教学要注重培养学生的创新意识并提高自主探究能力。由于当前高考具有较强的导向作用，对课程标准的创新要求最直接、最有效的贯彻方式是将其在高考中予以体现。因此各地区高考试题皆对探究能力和创新意识给予重视。但高考试题如何有效考察学生的创新意识和探究能力，虽然经过几年的探索已经取得不少成果，但毕竟还处于初级阶段，进一步深入地研究是必要的。

本文就2012年福建、北京、上海、四川、湖南、湖北及江西七省高考数学创新试题的分布和特点进行分析，启发一线教师透过现象看本质，“寻”规“导”矩，即“寻”出命题初衷，“导”出教学规律。数学创新性试题是指相对于特定使用对象而言，在试题背景、试题形式、试题内容或解答方法等具有一定的新颖性与独特性的数学试题，其基本目的在于培养或诊断特定使用对象的数学创新意识与创新能力[1]，笔者之所以选这七个省是因为其高考试题创新点比较明确。

1 创新试题的分布与启示

本文按照创新试题的界定，分别从题型、分值和所考察的知识点三个角度研究创新试题的分布，由表1不难发现，2012年高考数学创新试题分布具有如下特点：（1）创新题型多样化。创新试题灵活多样，不拘泥于形式，注重创新能力的考察；（2）知识点相对集中。知识点较集中分布在数列、不等式和函数等。（3）分值比重不大。高考是选拔性的考试，适当的创新题的呈现有助于创新人才的选拔，同时还要顾及成绩的正态分布，因此分值比重不宜过大。以上诸特点也给一线的教师以启示：（1）创新试题不等于“难题”。创新试题旨在考察学生创新意识和探究能力，这就要求教师教学中积极引导学生主动学习、独立思考，在探究和互动中获得知识；（2）重视不等于“拔高”。对学生探究能力和创新意识的培养控制在一定的范围和层次上，不能脱离实际教学和学生生活。因此，一味追求新和巧是不对的，这也是为什么不少教师考前对高考试卷充满期待，希望能够眼前一亮，而拿到后却觉得如此“亲切”，不禁有些“失落”；（3）有“迹”可循。创新试题知识点不是“苦海无边”，往往集中出现在能反映数、形运动变化的知识点，如，数列、函数、不等式、向量及几何等。

表1 各省创新题型分布、分值、题型及涉及知识点

2 创新点“寻”规“导”矩

2012年福建、北京等七省高考数学创新试题形式多样，内容丰富，但试卷的命制万变不离其“衷”,即旨在考查学生的创新意识和探究能力。基于对创新试题的既定，下面将从数学概念、试题背景和解题意识等三个方面“寻”规“导”矩。

2.1 新的数学概念

给出一个新的数学概念，这里的概念包括定义和性质，然后要求学生应用该概念解，这是一种最常见的创新题型。这类题型主要考察考生的数学阅读能力。这就要求学生能够对“原材料”分析、概括、建构起实质意义，并纳入到已有知识结构中[2]。如：

A.①② B.①③ C.②④ D.③④

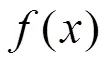
除此之外，北京理20、上海理23、江西理21这三个省份的压轴题均以新定义数学概念的面目出现，综合考查了函数、数列、不等式等多方面的知识与方法；湖北理7定义了一个新的函数：“保等比数列函数”；湖南理16则定义了一种数列的变换，考查了数列知识以及归纳推理能力，这也启发教师在教学中要注重培养学生的数学阅读能力。

2.2 新的试题背景

该类型试题给出现实生活中一些有意思的现象或事实，而这些现象或事实对学生来说熟悉而陌生，熟悉是因为学生经常遇到，陌生是因为大多数人没有从数学的角度思考过该问题。该种题型主要考察学生观察、分析和归纳能力，其关键能够把实际问题抽象为数学问题。如：

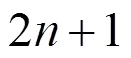
福建文16以道路规划为背景考查演绎推理，湖北理10以“开立圆术”为背景考查圆周率近似值的计算，以上各题均旨在考查学生抽象能力。因此教师教学中要激发学生从数学的角度感知生活的兴趣，注重学生探究隐藏在现象背后的数学知识，以及领会归纳与演绎、特殊与一般等数学思想方法。

2.3 新的解题意识

一般该类试题综合性较强，解题思路不唯一，但不同解题意识下的解题效率有很大不同。该类试题主要考察学生的发散思维能力。如福建理15不仅试题背景新颖，解决问题的思路多样，其新颖程度和巧妙程度能很好体现学生的创新意识和应用能力，实属创新题之典范。

方法一通过代数推演的方式求解，方法二充分利用图像所呈现的信息数形结合地求解，二者求解效率相差很大。该题作为一道高考填空压轴题，命题者的命题意图或许并不是“小题大做”。显然方法二更符合命题人的考查初衷。因此在实际教学中，教师要注意培养学生的发散思维能力，如，用运动与变化的观点来看待问题，有意识用多种方法解题，并比较其利弊，启发学生从数学思想方法角度思考其深层次逻辑关系，避免定势思维。

3 小结

高考“神圣”，但不“神秘”，“神圣”体现在其对社会和考生本身的意义，其不“神秘”体现在其考查的本意。高考数学也同样不能“神”化，尤其是创新试题。因此，备考创新试题注重以下几个方面：

（1）教学中太多的技巧呈现和规律总结无济于事，只会适得其反，大大限制学生发散思维和创新意识；

（2）补充太多的课外知识及知识背景无疑是画蛇添足，因为课外知识及其知识背景不可穷举，更何况这不是考试的初衷，只会增加学生负担；

（3）事实上，高考数学试题皆应立足数学的学科本质，着力考查考生综合运用数学知识分析、解决相关数学问题的能力。因此，教学应关注对学生“三基”的培养，以及创新思维能力的提高。

[1] 马老二.高中数学创新题编拟研究[D].西安:陕西师范大学，2010.

[2] 厉小康.数学阅读能力的培养研究[J].数学教育学报, 2004, 13(2): 89-92.