一个可积非线性演化方程的达布变换及其精确解

马云苓， 曾 昕， 耿献国

(1.商丘师范学院 数学系 河南 商丘 476000； 2.郑州大学 数学系 河南 郑州 450001)

0 引言

非线性演化方程在很多领域中都有重要应用，例如非线性光学、深水波理论和等离子物理中的许多问题都可以归结为非线性演化方程.因此，非线性演化方程的求解具有重要意义.在求解非线性演化方程的诸多方法中，达布变换[1-4]是一种非常有效的方法，它从非线性演化方程的一个平凡解出发能够求出一系列精确解[5-6].作者研究一个新的非线性演化方程

(1)

基于其Lax对和谱问题的规范变换，构造出该方程的一个达布变换，进而利用此达布变换，得到该方程的精确解，包括有理解、孤子解与周期解.

1 达布变换

构造出方程(1)的一个达布变换，考虑(1)的Lax对，即谱问题以及辅助问题

Lψ=λψ,ψt=Bψ,

(2)

式中，

L=∂4+4q∂2+(4qx+2r)∂+2qxx+4q2+qt+p,B=∂2+2q,

(3)

其中，q,r,p是3个位势，λ是1个常值谱参数.若ψ满足Lax对(2)，那么由Lax方程Lt=[B,L]，可得

qt=rx,rt=px,pt=-rxxx-8qrx-4rqx.

(4)

由Lax对(2)的相容性条件，可得方程(4)等价于方程(1).

定理1设λ=λ0,f满足Lax对(2)，A=-(lnf)x，定义规范变换

(5)

并且定义

(6)

(7)

其中，

(8)

证明通过直接计算可得

(9)

把(9)带入Lf=λ0f,得

(10)

对(10)关于x微分，可得

(11)

其中，

(12)

利用(5)及(2)的第一个表达式，得到

(13)

(14)

(15)

其中，

Q=4qx+2r.

(16)

2 精确解

下面利用达布变换(6)给出方程(4)的精确解.从(4)的一个平凡解(a,b,c)开始，其中，a,b,c是常数.把q=a,r=b,p=c和λ=λ0代入Lax对(2)中，可得

(17)

Ⅰ.当a=b=c=0，且λ0=0时，(17)有一个多项式解

f=c1x2+c2x+2c1t+c0,

(18)

其中，c0,c1,c2是任意常数.利用达布变换(6)，得到(4)的一个有理解

(19)

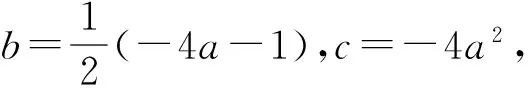
(20)

(20)有解

(21)

(22)

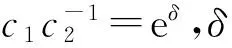
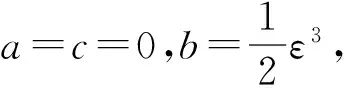
f=c1+c2exp(-εx+ε2t)+c3exp[-(β1+ε)x-γ2t]+c4exp[-(β2+ε)x-γ1t],

(23)

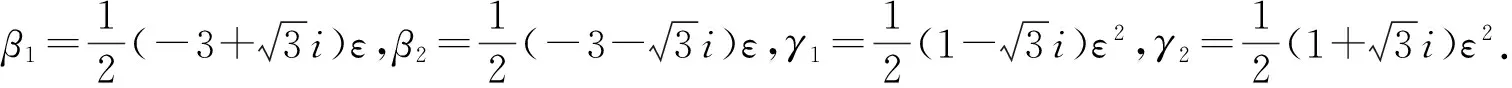
(24)

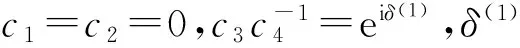
(25)

Ⅳ.当b=0,a,λ0,c都是实数，且λ0≥c时，方程(17)约化为

(26)

(27)

其中，ci(i=1,2,3,4)是任意常数.利用达布变换(6)，可得(4)的孤子解

(28)

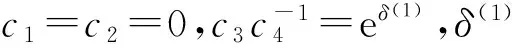
(29)

Ⅴ.当b=0,a>0,c=16a2,且λ0=4a2时，方程(17)有一个解

(30)

其中，ci(i=1,2,3,4)是任意常数.利用达布变换(6)，可得(4)的周期解

(31)

(32)

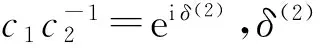
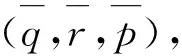
参考文献：

[1] Levi D.On a new Darboux transformation for the construction of exact solutions of the Schrödinger equation[J].Inverse Problems,1988,4(1):165-172.

[2] Gu Chaohao, Zhou Zixiang.On Darboux transformations for soliton equations in high-dimensional spacetime[J].Lett Math Phys,1994,32(1):1-10.

[3] Li Yishen.The reductions of the Darboux transformation and some solutions of the soliton equations[J].J Phys A: Math Gen,1996,29(14):4187-4195.

[4] Geng Xianguo.Darboux transformation of the discrete Ablowitz-Ladik eigenvalue problem[J].Acta Math Sci,1989,9(1):21-26.

[5] 李雪梅，杨运平.高阶耦合非线性Schrödinger方程的单孤子解[J].郑州大学学报：理学版，2002，34(3)：13-15.

[6] 杜殿楼.驻定CG方程解的参数表示[J].郑州大学学报：自然科学版，1998，30(1)：12-17.