量子神经网络在交通运输能力预测中的应用

贾花萍

0 引言

交通运输能力受许多因素影响，如发展水平、人口数量、自然条件等，而且还有季节性，如春运等，因此在建立预测模型的时候，在不影响精度的条件下，应该建立简单的模型，科学的对交通运输能力进行分析和预测，对促进运输资源优化配置，全面提高交通运输现代化水平，发挥各种运输方式的最大效率，促进交通运输业规范而高速的发展，加快交通现代化，具有十分重要的意义。[1]交通能力预测的方法很多，其中定量法常用的有移动平均法、指数平滑法、回归分析法，灰色预测方法和作为多种方法综合的组合预测方法。这些方法大都集中在对其因果关系回归模型的分析上，所建立的模型不能全面和本质的反映所预测动态数据的内在结构和复杂特性，与这些方法相比，神经网络有较强的映射能力、泛化能力、容错能力和很强的联想记忆能力，同时，也不需要建立函数模型，所以，用神经网络模型进行交通运输能力预测是一种有效的方法。[2]

自1995年美国的Kak教授首次提出量子神经计算[3-4]的概念以来，量子神经网络(Quantum Neural Network,QNN)受到了广泛关注.Purusho thaman G等[5]提出了基于多层激励函数的量子神经网络模型,模型隐层神经元激励函数采用多个传统激励函数的叠加,通过对模糊数据集的特征空间进行多级划分,快速响应了其特征空间的结构.理论和实践表明,量子神经网络模型对具有不确定性非稳态数据具有良好的预测效果[6-7].因此,本文根据QNN对不确定性非稳态数据的较好预测效果的优点,建立道路交通运输能力预测模型,在对原始数据进行相空间重构基础上,采用态叠加的激励函数,对道路交通运输能力数据的特征空间进行多层梯级划分,并在训练过程中动态调整量子间隔,对算法的预测效果进行考察。

1 道路交通运输能力预测模型的建立

1.1 量子神经元

神经网络函数逼近的正确特性是因为神经网络从输入到输出形成了一个非线性映射和激励函数存在一些饱和区域,然而传统的神经网络是使用两级激励函数的神经元构成的,这种激励函数的输出仅有两个饱和区,但是神经元中也可以采用具有多层饱和级别的激励函数,此时这种神经元被叫做量子神经元.将两层激励函数神经元的思想推广到多层激励函数的神经元,其激励函数，如图1所示:

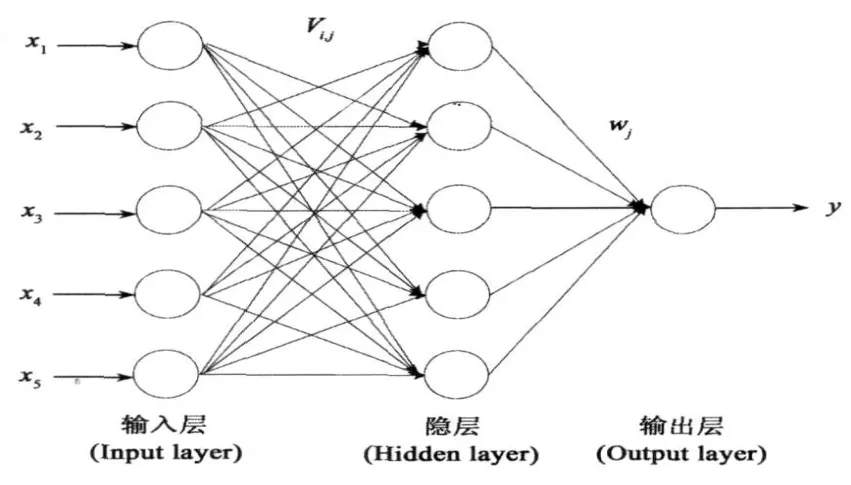
图1 预测模型结构图

1.2 基于量子神经网络的预测模型

提出的基于量子神经网络的道路交通运输能力预测模型由输入层、隐层和输出层以及各层神经元之间连接组成.由于导致道路交通运输能力的影响因素错综复杂,且影响因素之间的关系也不明确,因此就直接采用时间t作为变量来综合地代替这些因素，构成道路交通运输能力时间序列,作为预测模型的输入.由于预测效果受嵌入维数影响较大,依据相空间重构理论,当时间序列嵌入维数太低,难以恢复系统的演化行为和揭示其动力系统的内蕴,达不到预测的精度要求且网络不稳定;维数太高则收敛太慢容易陷于局部最小经反复试验,选取嵌入维数为6,确定输入层节点数为6,输入层激励函数为线性函数g(g),输入向量为6年内各年交通运输能力的时间序列.由于每次预测都是通过6年的历史交通运输能力数据计算新一年的数据,因此选取输出层节点数为1,输出层激励函数为线性函数g(g).隐含层神经元节点数的选取没有明确的规定,采用经验公式与试算法相结合的方法来确定隐含层节点个数.经验公式选取:其中n1表示隐含层节点数,n表示输入层节点数,m表示输出层节点数,a为[0,10]之间的常数.文中n=6,m=1,故隐含层神经元个数应该在3-13之间;再根据试算法来确定预测模型隐含层的确切节点数.这里隐含层节点数分别选择3、5、8和12,构成一个试验预测模型进行训练,并分别查看不同隐含层节点数对应的网络性能.通过比较不同隐含层节点数的训练误差曲线和不同隐含层节点数的误差得出当隐含层神经元个数为5(即n1=5)时,网络的收敛速度最快且误差较小.

1.3 训练算法

预测模型的训练算法仍采用梯度下降法,在每个训练周期中,训练算法不仅更新不同层神经元之间的连接权,而且更新隐层各神经元的量子间隔.权值的更新算法与常规BP网络更新算法完全相同.量子间隔的更新算法如下:

对模式类矢量Cm(m为模式类数目),隐层第i个神经元的输出方差为对模式类矢量Cm(m为模式类数目),隐层第i个神经元的输出方差为

其中him当前网络输入向量为xk时隐层第i个神经元的输出；类cm基数。

2 应用实例

用2000-2005共6年的历史统计数据作为网络训练样本，2006-2009年的数据作为测试样本，如表1所示:

表1 数据样本

将训练样本带入预测模型，与BP神经网络预测结果比较，如图2所示:

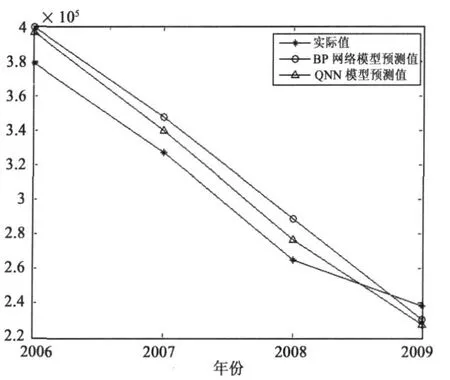
图2 预测结果比较

3 研究结论

道路交通运输能力预测是道路交通研究的一项重要内容.本文为道路交通运输能力预测提供了一种基于量子神经网络的预测模型,有效提高了道路交通运输能力的预测.

[1]刘立明.分形法在河北省高速公路规划中的应用[J].河北工业大学.成人教育学院学报，2001,(19):93-98

[2]丁俊，孙洪泉分形维数测定方法对比分析[J]，苏州科技学院土木工程学院.2010,(5):55-59

[3]Kak S.,“On Quantum Neural Computing”,Information Science,V0L.83:143-160,1995

[4]Kak S.,“Quantum Neural Computing”， Advances in Imaging and Electron Physics，V0L.94:259—313，1995

[5]Purushotham an G,Karay iannis N B.Quantum neural networks:Inherently fuzzy feedforward neural networks[J].IEEE Trans.on Neural Networks,

[6]1997,8(3):679-693.

[7]Behm an E C,Chandrashka rV G,W ang C K.A quan tum neura l network computes en tang lement[J].Physi Cal Review Letters,2002,16(1):152-159.

[8]Benne tt C H,S teck J E,B ehrm an E C.Quantum information and computation[J].Nature,2000,404(3):247-255.