赏析2011年“华约”自主招生物理试题第15题*
许冬保
(江西省九江市第一中学,江西 九江 332000)
2011年“高水平大学自主选拔学业能力测试”(英文名称是Advanced Assessment for Admission,简称“AAA测试”),是由清华大学、中国人民大学、上海交通大学、西安交通大学、南京大学、浙江大学、中国科技大学组成的七校联盟,共同发起且委托专业考试机构组织的高中毕业生学业能力测试,俗称“华约”自主招生考试.自主招生考试的命题指导思想是:“不以超出中学大纲为考查目的,但也可能有少量试题会超出中学教学要求”.旨在通过自主招生考试,对那些具有极大发展潜能的考生甄别选拔出来.[1]下面对通用基础测试—自然科学中的物理部分试题第15题进行分析,以飨读者.
1 试题
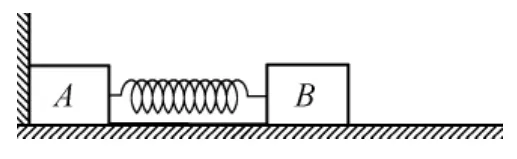
图1
如图1所示,质量分别为m和3m的物块A、B用一根轻弹簧相连,置于光滑水平面上,物块A刚好与墙接触.现用外力缓慢向左推物块B使弹簧压缩,然后撤去外力,此过程中外力做功为W.求:
(1)从撤去外力到物块A离开墙壁的过程中,墙壁对物块A的冲量;
(2)在物块A离开墙壁后的运动过程中,物块A、B速度的最小值.
2 常规解法—能量与动量的观点分析
(1)外力对物块B做功,使弹簧的弹性势能增加.撤去外力,压缩的弹簧将物块A压在墙壁处不动,弹簧的弹性势能转化为物块B的动能.当弹簧恢复原长时,设物块B的速度为v,由动能定理,有
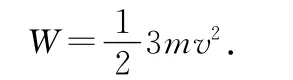
从撤去外力到物块A离开墙壁的过程中,墙壁给物块A以冲量,由动量定理,有
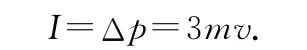
(2)物块A离开墙壁之后,在物块A、B通过弹簧相互作用的过程中,设某一时刻,物块A、B的速度分别为vA、vB,弹簧的弹性势能记为ΔEp.取物块B初始速度v的方向为矢量的正方向,由动量守恒定律及机械能守恒定律,有
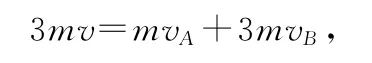
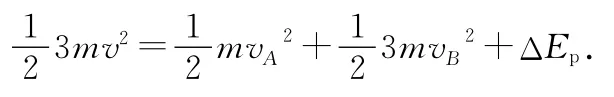
弹簧达自然长度时,物块的速度有最值,因此弹簧的弹性势能ΔEp=0.
联立解得
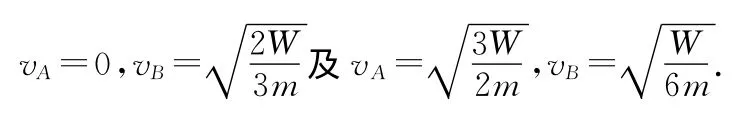
因此,在物块A离开墙壁后的运动过程中,物块A的最小速度为0,物块B的最小速度为
3 另类解法1—质心参考系中分析
对第(2)问,由动量守恒定律,可求得质心的速度vC.
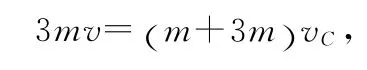
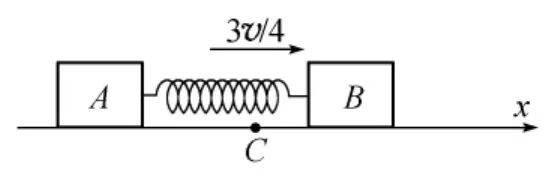
图2
在质心参考系中,物块A、B均作简谐运动.如图2所示,选择质心的速度方向为矢量的正方向,物块A离开墙壁的时刻记为t=0,两物块A、B的速度vA′、vB′与时间t的关系为
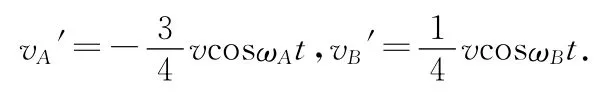
质心C两侧弹簧劲度系数分别记为kA、kB,则上式中
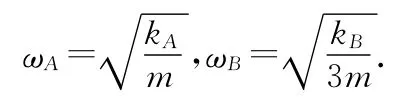
kA、kB与弹簧劲度系数k之间的关系满足
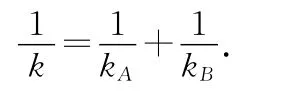
在质心参考系中,某时刻两物块的坐标满足
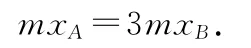
物块A、B相对质心运动的过程中,某时刻有
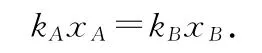
联立解得
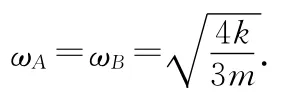
因此,在地面参考系中,两物块A、B的速度表达式分别为(取ωA=ωB=ω)
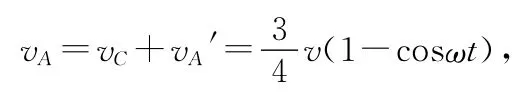
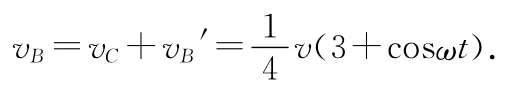
可见,vA与vB表达式中有一个共同的常数项3v/4,这正是质心的速度,即系统整体的运动速度.vA与vB表达式中还有一个方向相反的余弦项,它表示滑块A与B相对于质心各作简谐运动,其相位正好相反.由于因此,两物块的速度方向均向右,不可能向左.
4 另类解法2—非惯性参考系中分析
4.1 相对动力学方程的推导[2][3]
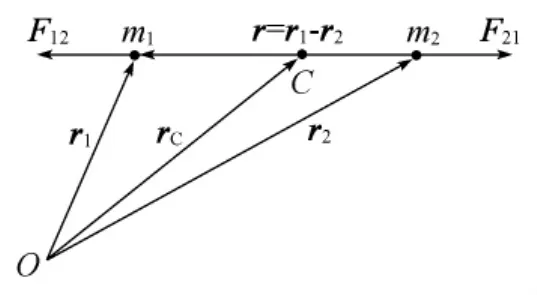
图3
如图3所示,设O为惯性系中固定点,质点m1、m2相对O的位置矢量分别为r1、r2(黑斜体字母表示矢量,下同).假设质点2施于质点1的作用力记为F12,质点1施于质点2的作用力记为F21,F12、F21遵循牛顿第三定律,即F12=-F21.
由牛顿第二定律,分别列出质点1、质点2的动力学方程
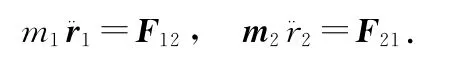
两质点均在运动.如果取质点2为平动的参考系,研究质点1相对于质点2的运动,相对径矢为r=r1-r2.计入惯性力则质点1的动力学方程为
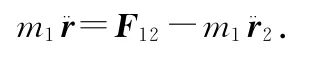
对该式变换,即
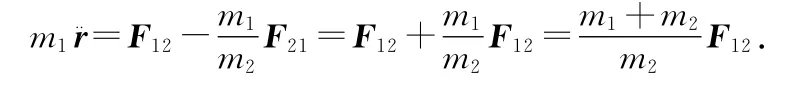
4.2 相对动力学方程分析
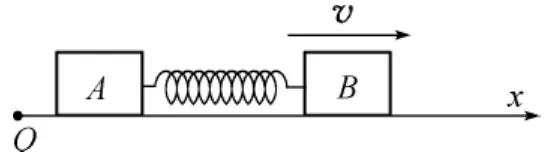
图4
对第(2)问,用相对动力学方程求解.题中两物块系统虽不孤立,但在竖直方向合外力为零,对物块运动没有影响,与孤立情况无异.因此可视为孤立两体问题用相对动力学方程求解[4].
选择地面为参考系,取物块B初始运动的方向为x轴,向右为正,如图4所示.某时刻t,物块A和B的坐标分别记为xA和xB.
研究质心x0的运动,质心坐标为
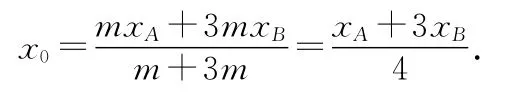
系统所受合外力为0,由质心运动定律知质心速度不变.上式对时间求导可得质心速度为
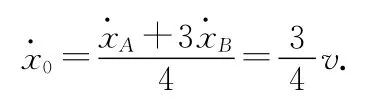
以物块A为参考系,研究物块B相对于物块A的运动.在此参考系中,将坐标原点取在弹簧既不伸长也不缩短时物块B所在的位置,如图5所示.某时刻t,设物块B的坐标为xB′,滑块B所受的合外力为弹簧的弹性力F=-kxB′.由相对动力学方程得式中,约化质量为
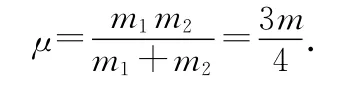
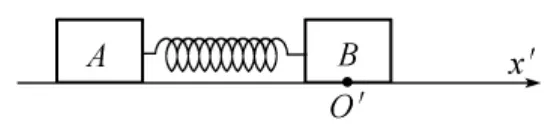
图5
于是相对动力学方程改写为
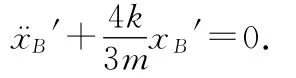
这是典型的谐振动微分方程,其解为
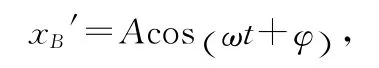
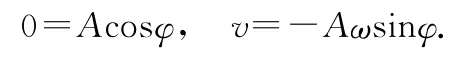
于是滑块B相对于滑块A的运动位移
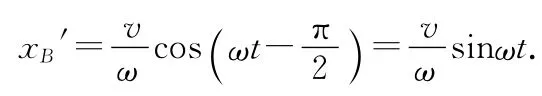
对上式求导,即得滑块B相对于滑块A的运动速度
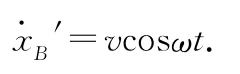
回到地面参考系,并利用质心速度表达式可得
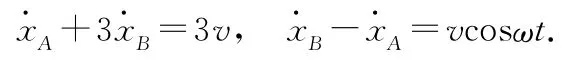
解得
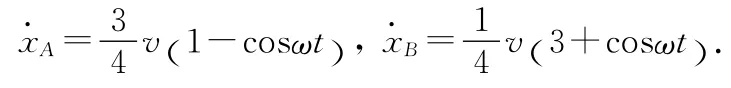
以下讨论同另类解法1.
说明:应用相对动力学求解时,还可以类比水平弹簧振子模型进行简化处理,过程如下:
在物块A离开墙壁后的运动过程中,以A为参考系,类比水平弹簧振子模型,B相对A作简谐运动,则B相对A的速度与时间t的关系为
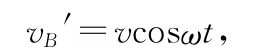
对系统由动量守恒定律,有
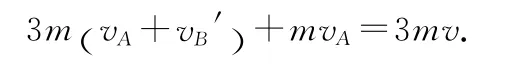
解得
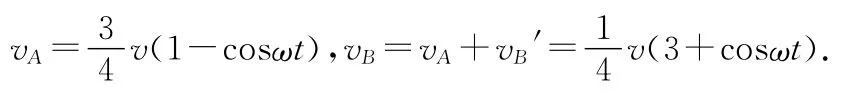
所得结果同上.
5 进一步探究的问题
试题还可以增加以下探究问题:
(1)在物块A离开墙壁后的运动过程中,试画出两物块A、B的速度图像.
由两物块A、B的速度表达式,可画出速度图像,如图6所示.由图像可以发现:物块A与B交替地拉推.每逢的奇数倍时,弹簧处于最长或最短状态,且两物块的速度相等;每逢的偶数倍时,弹簧处于自然长度,且两物块的速度取最值.由图像还可求得A、B两物块的最大速度分别为
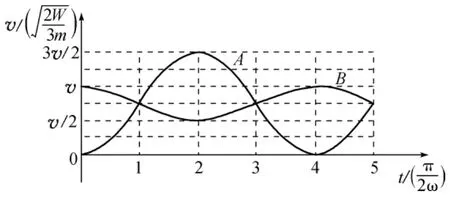
图6
(2)在物块A离开墙壁后的运动过程中,已知弹簧的劲度系数为k,则撤去外力后弹簧的最大伸长量x=?
设弹簧达最大伸长时两物块速度为v′,由系统机械能守恒定律,有
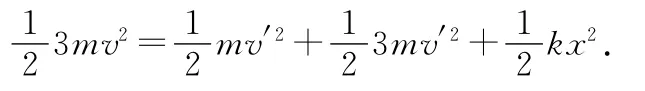
初态时,外力做功,弹簧的弹性势能增加,弹簧压缩量为x0,则由功能关系,有
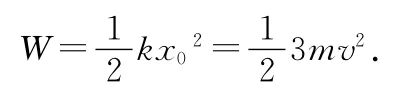
弹簧达最大伸长量时,由动量守恒定律,有
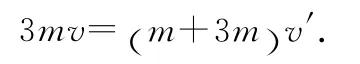
解得
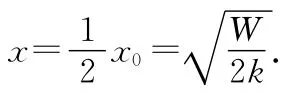
(3)在物块A离开墙壁后的运动过程中,探究A、B两物块的位移随时间变化的关系.
对两物块的速度对时间积分,有
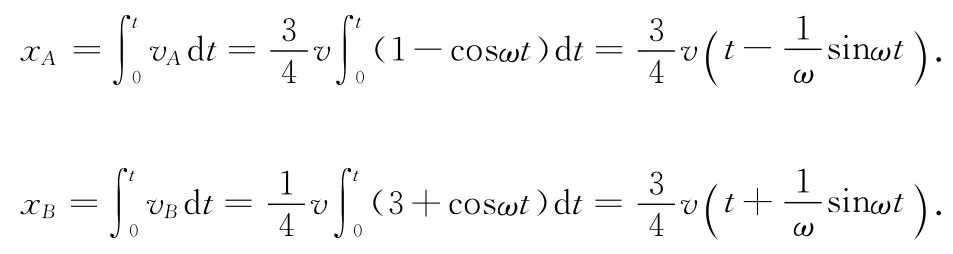
综合以上分析,试题考查的是力学中的一类典型问题.通过定性分析知道弹簧在自然长度状态时物块出现速度的最小值,可以从能量及动量的角度求解.在另类解法中,分别从质心参考系及非惯性参考系出发研究两物块的运动,深入问题的本质,揭示两物块运动的规律,从更高的视角来审视两物块的运动.这有利于学生分析问题和解决问题能力的提高.
1 于永建.大学自主招生物理命题特点与备考策略.中学物理教学参考,2011(10):2
2 郑永令.二体问题与折合质量.物理教学,2011(1):5-8
3 蔡伯濂.力学.湖南:湖南教育出版社,1985:196-197
4 梁昆淼.力学(上册 第四版).北京:高等教育出版社,2010:181-188
——兼谈参考系与坐标系的关联关系

