Chaos of discrete dynamical systems in complete metric spaces
ZHAI Hongli, LIN Yajing, SUN Bo
Chaos of discrete dynamical systems in complete metric spaces
ZHAI Hong-li, LIN Ya-jing, SUN Bo
(College of Mathematics and Computers, Changsha University of Science and Technology, Changsha 410114, China)
Chaos of discrete dynamical systems in metric spaces was discussed. Two existing criteria for chaos was improved, and it is proven that a system was topologically conjugate to a symbolic dynamical system if it has a regular degenerate snap-back repeller.
Metric space; discrete dynamical system; chaos; snap-back repeller
Consider the following discrete dynamical system:
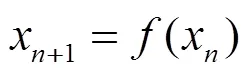
Chaos for interval maps or one dimensional discrete dynamical systems have been studied by T.Y. Li, J. A. Yorke, Goong Chen and other authors[1-4]. Chaos for n-dimensional discrete dynamical systems was first studied by F. R. Marotto, then by Li, Chen, Hsu S and Zhou[5-7]. In 2004, Y. Shi and G. Chen studied system (1) for general metric spaces, and obtained results as follows.




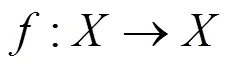


In this paper, we aim to modify Shi's work and deduce chaos of discrete dynamical systems in complete metric spaces under fewer conditions. We modify Proposition 1, and obtain the same chaos results under condition (a) and (b). Then we modify Proposition 2, and prove that the discrete dynamical system is chaotic under condition (a). Finally, we simplify Proposition 3 and get a better one.
This paper is organized as follows: In section 1 we recall some preliminary definitions and lemmas; In section 2 we state our main results and prove them.
1 Definitions and lemmas
For convenience, we recall some definitions and lemmas as follows[3,8]:
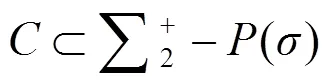

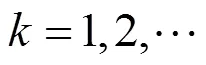


2 Main results
Proof The proof is similar to that of Yuming Shi (Ref. [8], Theorem 1). So we recall the main steps of Yuming Shi, and modify a key step.
The proof is divided into three steps:


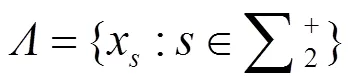
Combining Proposition 6 and the arguments on Theorem 1, we have:

Acknowledgements
The research for this work was supported, in part, by the Natural Sciences Council of China.
[1] Roger Temam. Infinte-Dimensional Dynamical Systems in Mechanics and Physics[M]. New York: Springer-Verlag, 1998.
[2] Li T Y, Yorke J A. Period three implies chaos[J]. American Mathematical Monthly, 1975, 82: 985-992,.
[3] Chen G, Huang T, Huang Y. Chaotic behavior of interval maps and total variations of iterates[J]. Int J Bifur chaos, 2004, 14: 2161-2186.
[4] Zhou Z L. Symbolic Dynamical Systems[M]. Shanghai: Shanghai Science and Technology Press, 1997.
[5] Sun B, Xiao H, Zhang X. A note on chaotic behavior of interval maps[J]. J Physics: Conference Series, 2008, 96: 1-4.
[6] Frederick R. Marotto. Snap-back repellers imply chaos inR[J]. J Math Anal Appl, 1978, 63: 199-223.
[7] Chen G, Hsu S, Zhou J. Snap-back repellers as a cause of chaotic vibration of the wave equation with a Van der Pol boundary condition and energy injection at the middle of the span[J]. J Math Phys, 1998, 39: 6459-6489.
[8] Li C, Chen G. An improved version of the Marotto Theorem[J]. Chaos, Solitons and Fractals, 2003, 18: 969-977.
[9] Shi Yuming, Chen Guanrong. Chaos of discrete dynamical systems in complete metric spaces[J]. Chaos, solitons and fractals, 2004, 22: 555-571.
完备度量空间中离散动力系统的混沌
翟红利,林亚静,孙 波
(长沙理工大学 数学与计算科学学院, 湖南 长沙, 410114)
考虑度量空间中离散动力系统的混沌, 改进了两条现有判据, 证明了当一个系统有正则退化snap-back repeller时拓扑共轭于符号动力系统.
度量空间; 离散动力系统; 混沌; snap-back repeller
O 193
1672-6146(2012)01-0001-04
10.3969/j.issn.1672-6146.2012.01.001
2011-10-24
翟红利(1987-), 女, 硕士研究生, 研究方向为动力系统与控制理论.
孙波(1965-), 男, 博士, 教授, 主要研究方向为偏微分方程、动力系统与控制理论. E-mail:sunbo52002@ yahoo.com.cn
(责任编校:刘晓霞)

