具Gilpin-Ayala模型的正解唯一性与周期吸引性

张俊杰, 马满军



具Gilpin-Ayala模型的正解唯一性与周期吸引性

张俊杰1, 马满军2

(1 南华大学 数理学院, 湖南 衡阳, 421001; 2 中国计量学院 理学院, 浙江 杭州, 310018)

利用上下解原理、最大值原理及分析技巧, 研究了一类具有驱动扩散的Gilpin-Ayala模型, 获得该模型正解的存在唯一性, 以及周期吸引性的充分条件.

上下解原理; 最大值原理; 一致椭圆性

本文考虑具Gilpin-Ayala模型如下:

1 定义与引理

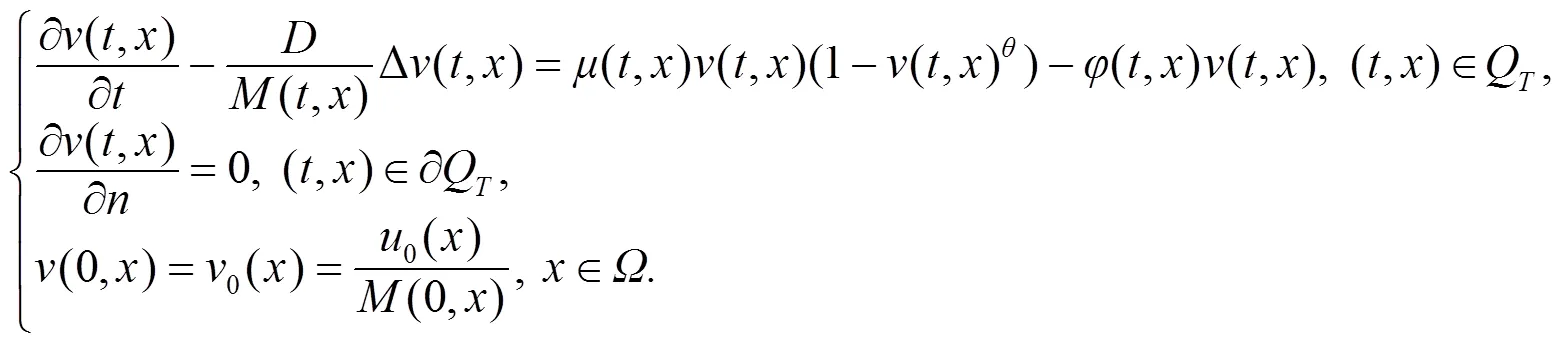
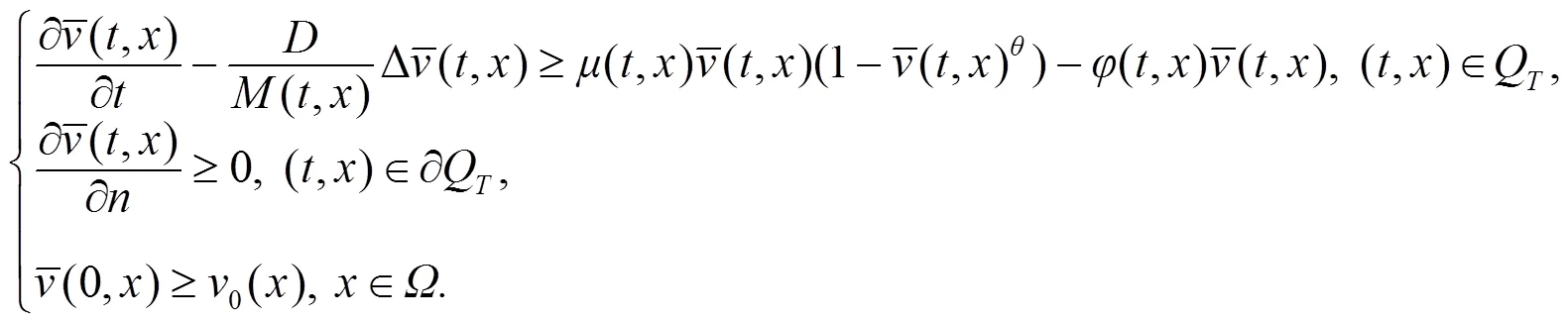
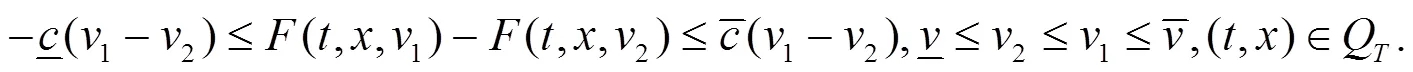
为了构造式(2)的上下解序列, 引出定义2.

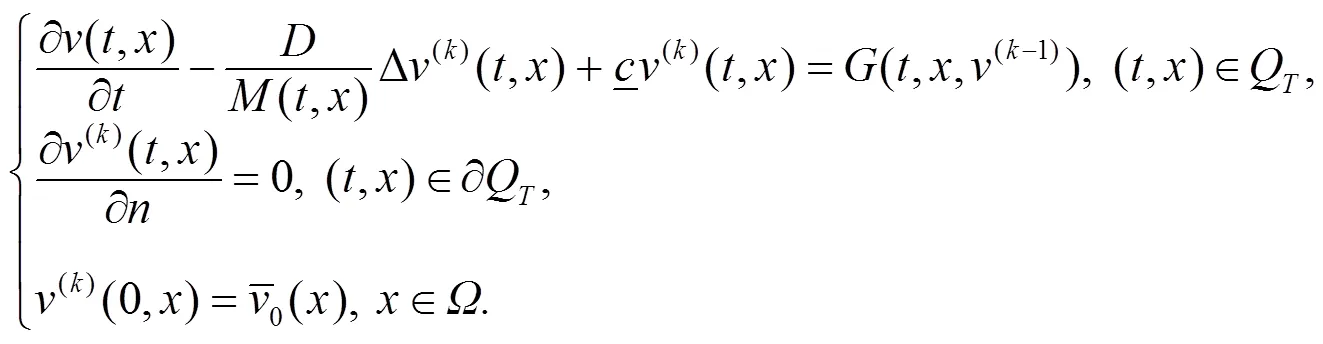
在上述有关假设和定义基础下, 由文献[1]中偏微分理论知识可得引理1-3.

以及初值条件:

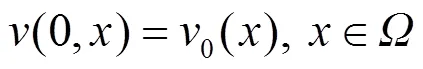
关于引理4的一般证明过程可参看文献[2]中定理3.2, 这里不再证明.

2 主要结果及证明

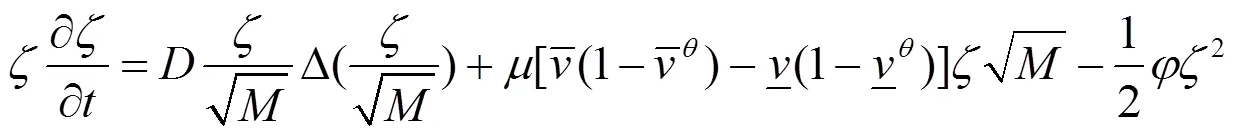
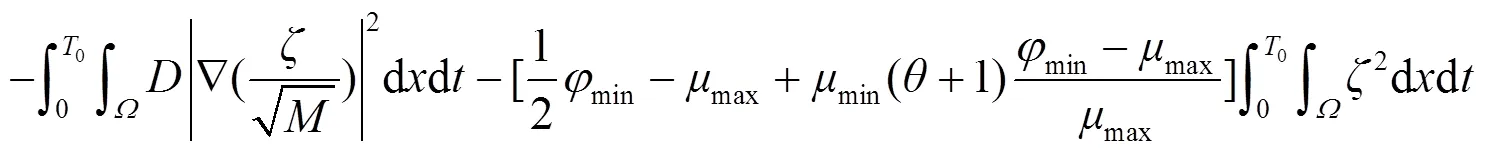
[1] Pao C V. Nonlinear parabolic and elliptic equations[M]. New York: Plenum, 1992.

[2] Zhou L, Fu Y. Existence and stability of periodic quasisolutions in nonlinear parabolic systems with discrete delays[J]. J Math Anal Appl, 2000, 250: 139-161.

Uniqueness and attractance of positive periodic solutions in Gilpin-Ayala

ZHANG Jun-jie1MA Man-jun2

(1 School of Mathematics and Physics, University of South China, Hengyang 421001, China;2 College of Sciences, China Jiliang University, Hangzhou 310018, China)

This paper is devoted to the studyGilpin-Ayala model with driven diffusion by applying the method of upper and lower solution and the maximum principle and other analytical techniques. Existence and uniqueness of positive solutions and sufficient conditions for the attractivity of positive periodic of this model are obtained.

the method of upper and lower solution; the maximum principle; uniformly elliptic

O 175

1672-6146(2012)01-0007-04

10.3969/j.issn.1672-6146.2012.01.003

2011-12-08

张俊杰(1986-), 男, 硕士研究生, 研究方向为微分方程与动力系统. E-mail: zhangjunjie55@163.com

(责任编校:刘晓霞)