三级物流服务供应链能力协调

朱卫平，刘伟，高志军

(1.上海海事大学交通运输学院，上海 201306;2.中国计量学院经济与管理学院，杭州 310018)

0 引言

作为一类典型的服务供应链，物流服务供应链正成为供应链与服务管理研究的新领域，其产生背景是某一物流服务企业在自身不能独立完成服务运作的情况下，需要从其他企业采购相应的服务能力并形成物流服务组合以完成物流功能运作.［1］由于物流服务供应链是一个新兴领域，目前的研究主要集中在两级物流服务供应链的能力协调方面，比较成熟的研究成果也主要集中在产品供应链协调机制方面.KIRSTIN［2］研究具有不确定交货特征的供应链协调问题，分析生产商和供货商彼此独立和集中决策两种协调模式下的最优决策行为.黄小原［3］在此基础上运用主从决策理论进一步研究不确定需求情况下供应链数量协调机制，并利用离线遗传算法进行求解，获得满意的协调效果.孙荣庭等［4］研究销售商存在竞争的1∶n结构的供应链，基于古诺模型提出一种线性契约解决多销售商竞争的协调问题，并证明其所设计的协调机制可以获得集中协调机制下的供应链绩效水平.BERNSTEIN等［5］研究面向随机需求，且需求分配价格敏感情况下的销售商横向竞争的协调问题.CHEN等［6］针对单个供应商和多个零售商组成的供应链系统，研究市场需求扰动时供应链的不同协调模式.马士华等［7］以MTO型供应链为背景，建立时间价格敏感需求下的分散决策和集中决策的协调模型，并对两种协调模型进行优化求解.HSIEH等［8］研究需求和供给双方不确定情况下，由单一原材料供应商、设备制造商和销售商组成的分散式供应链的协调优化问题.刘伟华等［9］考虑具体物流服务供应链中存在物流能力匹配的要求，基于Stackelberg博弈模型，建立有/无能力约束的利润和成本模型，进一步证明无能力匹配情况下供应链相对更具成本和利润优势.YAN等［10］和CHOI等［11］采用信息更新的方法，集中分析多个阶段采购成本变动情况下的产品供应链协调与数量决策问题，为成本信息分阶段变动的供应链协调问题提供一种新的研究思路，之后又有部分学者将这种方法引入服务供应链协调的研究之中.桂云苗［12］和王晓立等［13］研究需求和供给不确定情况下两级物流服务供应链的能力协调问题.崔爱平等［14］提出一种基于期权契约的协调机制，研究其在主从博弈下如何对集成商和分包商的能力订购和投资决策进行有效协调的问题，并对供应链期望额外利润分配和协调机制效果进行数值检验和分析.

上述典型研究主要是基于固定和变动需求背景下，以成本、价格、交货期等为扰动因素的产品供应链协调机制为主，而在物流服务供应链领域主要以两级物流服务供应链的能力协调为主［9，12－15］.有关三级物流服务供应链的研究仅见于文献［16］，该文提出一种公平熵描述利润分配原则，构建随机需求环境下物流服务供应链节点成员间收益共享系数的确定方法.本文以三级物流服务供应链为对象，研究在需求不确定情况下由单一物流服务集成商R，功能型物流服务提供商F和物流能力分包商S组成的三级物流服务供应链协调问题.

与产品供应链的协调机制不同，物流服务供应链具有两个基本特征:(1)物流能力的不可储存特性;(2)在整个物流服务供应链中，集成商居于主导地位，直接与终端市场接触.

基于这两个基本特征，首先引入市场需求这个随机变量(该变量对价格敏感)，然后对不同协调方式取得最优绩效的条件进行分析，最后通过详细的数值实验分析需求、成本因素以及市场风险对不同协调模式的影响.

1 问题描述及模型建立

1.1 问题描述

在三级物流服务供应链中，R，F和S的关系为:R根据市场需求n向F进行物流能力采购，F根据自身能力将部分物流能力外包给S.R直接面对终端客户，其终端物流市场的需求具有不确定性，假设其服从某一概率分布f(n)，且n对价格敏感.R需要对其物流能力销售价格P进行决策，同时根据对n的预测，确定向F采购的能力数量QR;F观测到R采购的能力数量后，基于自身利润最大化目标确定其能力销售价格R，同时，由于其能力限制，向S外包物流能力数量QF;S根据F外包的物流能力数量及其自身成本函数确定其销售价格W.为便于讨论，参照文献［16］，假设F将R订购的物流能力数量全部向S进行外包，即QR=QF=Q.

1.2 符号说明及技术假设

为研究方便，定义相关符号和技术假设如下:P为R向市场提供物流服务能力的销售价格;Q为R向F采购的物流能力数量;R为F向R提供的物流能力销售价格;W为S向F提供的物流能力销售价格;G为当R采购的物流能力不能满足市场需求时的单位能力机会损失成本;CS=cSQ+eSQ2为S的成本函数(根据文献［17］，CS包含基础物流能力固定成本和物流服务能力集成与运作管理的成本);CF=eFQ2为F的成本函数(根据文献［17］，CF主要来源于多种服务能力集成管理的成本);ΠR，ΠF，ΠS和ΠSC分别为R，F，S和供应链的期望利润函数.其中，P ＞R ＞W ＞0，G ＞0，cS＞0，eS＞0，eF＞0.

技术假设1:物流服务市场是完全竞争的，R面临不确定性需求n，n的概率分布函数f(n)已知，在［n－θ，n+θ］(θ为需求波动系数，θ＞0)上服从均匀分布.

技术假设2:R预期的n是P的线性函数，满足n=D－kP，其中D表示一定时期内的市场规模，k＞0表示价格敏感系数，因此R确定不同的物流服务价格将引起n的变动.

技术假设3:F和S不会出现能力不足的情况.

技术假设4:在三级物流服务供应链中，各节点成员都是风险中性的.

1.3 基本模型建立

根据上述参数设定及技术假设，将R，F及S的期望利润函数表示如下:

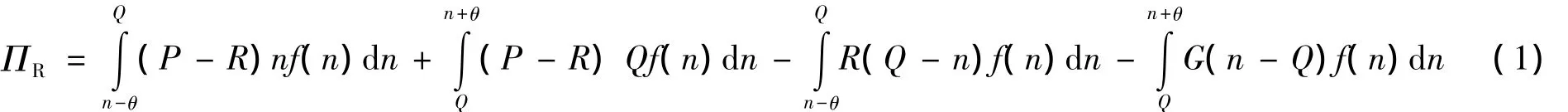
在R的期望利润函数中:第1项和第2项分别是市场需求量低于和高于能力订购量的收益;第3项为能力订购量高于市场需求量的损失(不同于产品供应链，服务产品具有无形性和易逝性，所以不产生库存也没有残值);第4项为能力订购数量少于市场需求时的机会损失成本.

2 不同协调模式分析

2.1 主从协调模式

主从(Leader－Follower，L－F)协调是物流服务供应链比较常见的协调方式，在这种协调方式下R掌握客户重要信息和市场需求状况，属于主导方，F和S是跟随方.R首先进行决策，F观察到R的决策后跟随决策，最后S进行决策.以下基于L－F协调模式，分析各节点企业最优决策的条件.

根据逆向归纳原理，首先对式(3)求Q的一阶条件，得

将式(4)代入式(2)，并求ΠF的一阶条件，得

将式(4)和(5)代入R的期望利润函数，通过ΠR的一阶条件，可得R的最优价格P*和最优采购数量Q*.满足以下两个条件时，R获得最大期望利润:

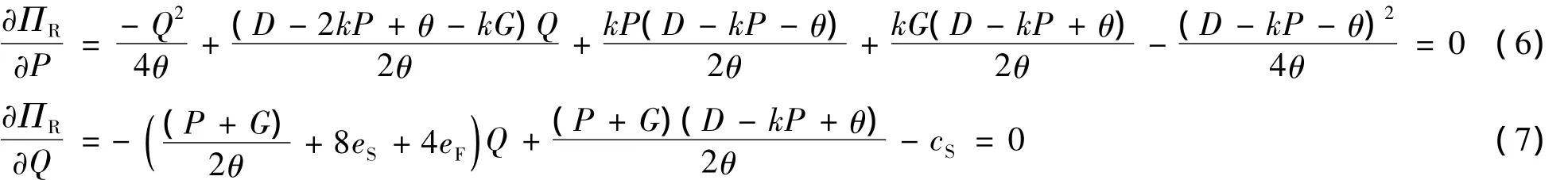
根据式(4)～(7)可求得 R，F和 S的最优策略((P*，Q*)，R*，W*)，将其代入各自期望利润函数可得到各自最优期望利润.

2.2 集中协调模式

在这种协调方式中，由R，F和上游S构成的三级物流服务供应链中，各成员实现信息共享，利用全部信息进行统一决策，实现系统整体利润最大化.在这种情况下整个物流服务供应链的期望利润函数为

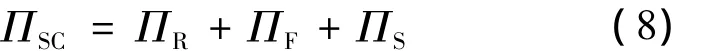
由式(1)～(3)得

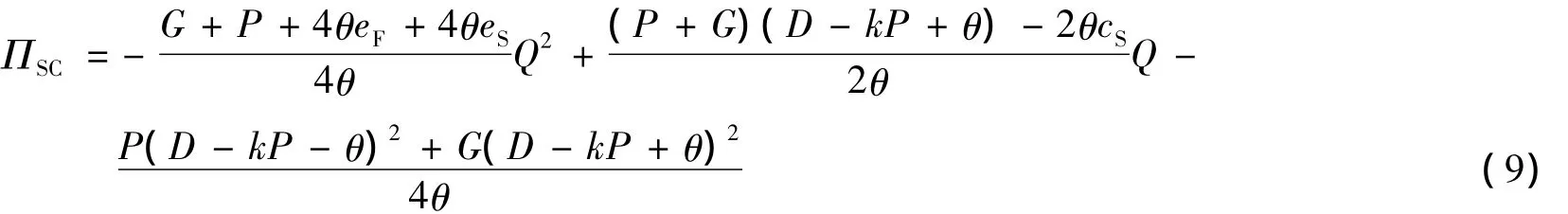
命题1在集中协调模式中，当θ≤k2M(eS+eF)+kM(M=P+G)时，ΠSC存在最大值.

证明物流服务供应链期望利润ΠSC存在最大值，必须满足以下条件

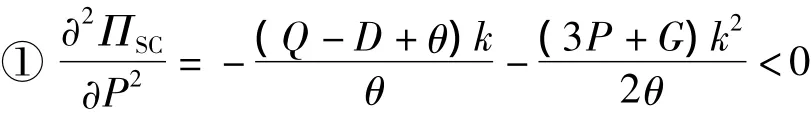
由Q∈［n－θ，n+θ］，n=D －kP，易得条件①成立;由各基本参数取值范围知，条件②显然成立;分别将Q=n－θ和Q=n+θ代入条件③，使该式成立，可得θ≤k2M(eS+eF)+kM，其中M=P+G.证毕.

从整体物流服务供应链期望利润函数可以看出，在进行集中协调时，F的销售价格R与S的销售价格W对整体物流服务供应链的期望利润没有影响，R和W主要调节整个供应链内部不同节点企业的利润分配.在相关参数满足条件①～③的前提下，整个供应链的最优销售价格P*和采购数量Q*满足以下两个条件时，集中协调取得最优的系统期望利润

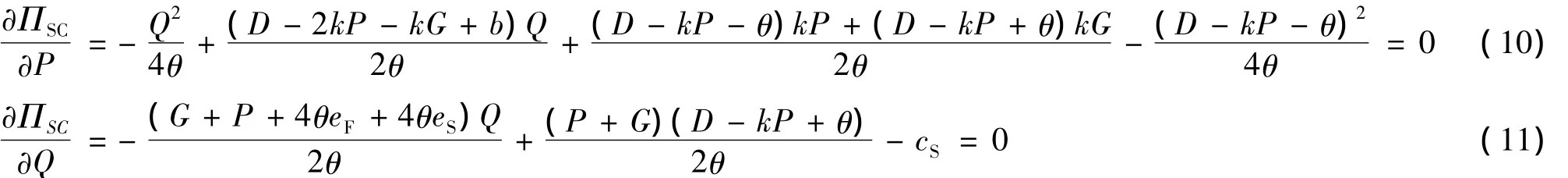
根据以上两式求得集中协调下的系统最优策略(P*，Q*)，将其代入期望利润函数可得集中协调下的最优期望利润.

2.3 数量协作联盟协调模式

命题2在R，F和S分散决策情况下，各自都基于自身期望利润最大化的目标进行决策，物流集成商根据市场需求预测决定P和Q，F和S决定提供R和W的能力.在这种情况下，若三方通过相互协商，可以使R希望采购的能力数量与F愿意提供的数量以及S最终提供的数量一致，本文定义这种协调模式为数量协作联盟.

证明首先，根据R期望利润函数公式(1)，同命题1证明相似，当θ≤kG时，ΠR存在最大值.

在R的期望利润函数存在最大值的基础上，其决策变量(P，Q)满足以下一阶条件时，R获得最优期望利润

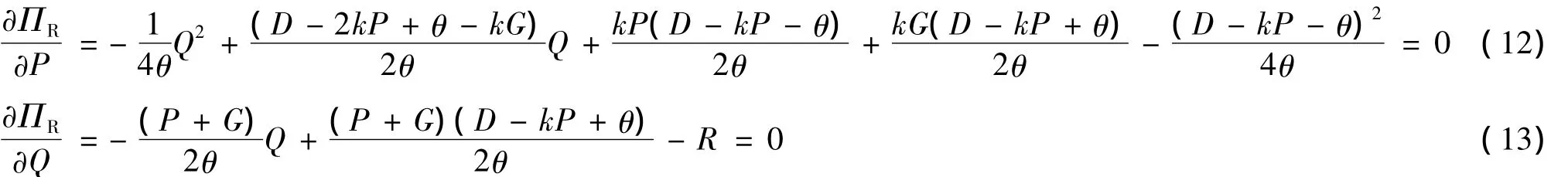
根据式(13)，R希望采购的能力数量

根据F期望利润函数式(2)，对其求一阶条件得F提供的能力数量

同理，根据S期望利润函数式(3)，对其求一阶条件，得S可提供的能力数量:

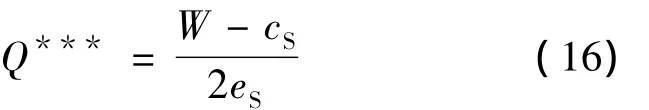
三级物流服务供应链可通过内部节点企业物流能力转移R与W的调整，使得三者能力数量需求和供给达到一致，这种协调模式有别于传统的收益共享或者数量回购协调模式，它无须借助外部新增契约参数，主要通过内部节点企业基于竞争协商的方式达到整体绩效的提升.

3 数值实验分析

为进一步考察三级物流服务供应链不同协调模式对整体绩效的影响，通过一系列详细的数值实验，对比分析不同协调模式的有效性.数值实验按前文所分析的3种协调模式分别建立数学模型，用MATLAB 7.0编程求解.为分析不同协调模式中k，θ，eS，cS，eF对三级物流服务供应链中各成员期望利润及不同供应链成员最优价格的影响，分别将上述参数在一定取值(见表1)下供应链各成员的期望利润进行对比，表2～8为所有数值实验结果.

表1 三级物流服务供应链相关基础参数取值

根据表2～8的实验结果，得到相关结论如下:

(1)随着k的增加，在L－F协调模式和数量协作联盟模式下，R，F和S的最优定价以及R的最优采购数量均下降;同时，整体供应链绩效也下降.这说明随着k增加，市场对价格越敏感，物流服务供应链中各成员为规避市场不确定性带来的风险，会选择降低各自的决策数量.

(2)θ增加时，在L－F协调模式和数量协作联盟模式下，R的P和Q，F的R及S的W都增加，这说明随着需求波动的加大，供应链各成员为确保自身的期望收益，都会不同程度地提高各自的决策值.

表2 k对不同协调模式下供应链绩效的影响

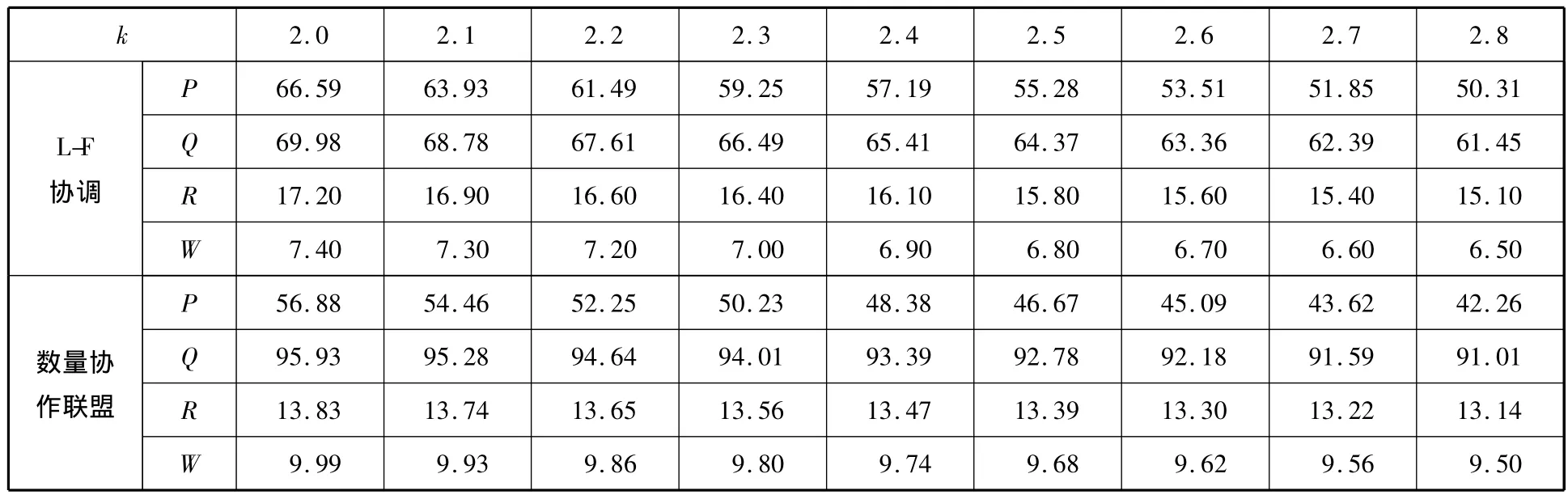
表3 k对不同协调模式下物流服务供应链各成员最优价格的影响

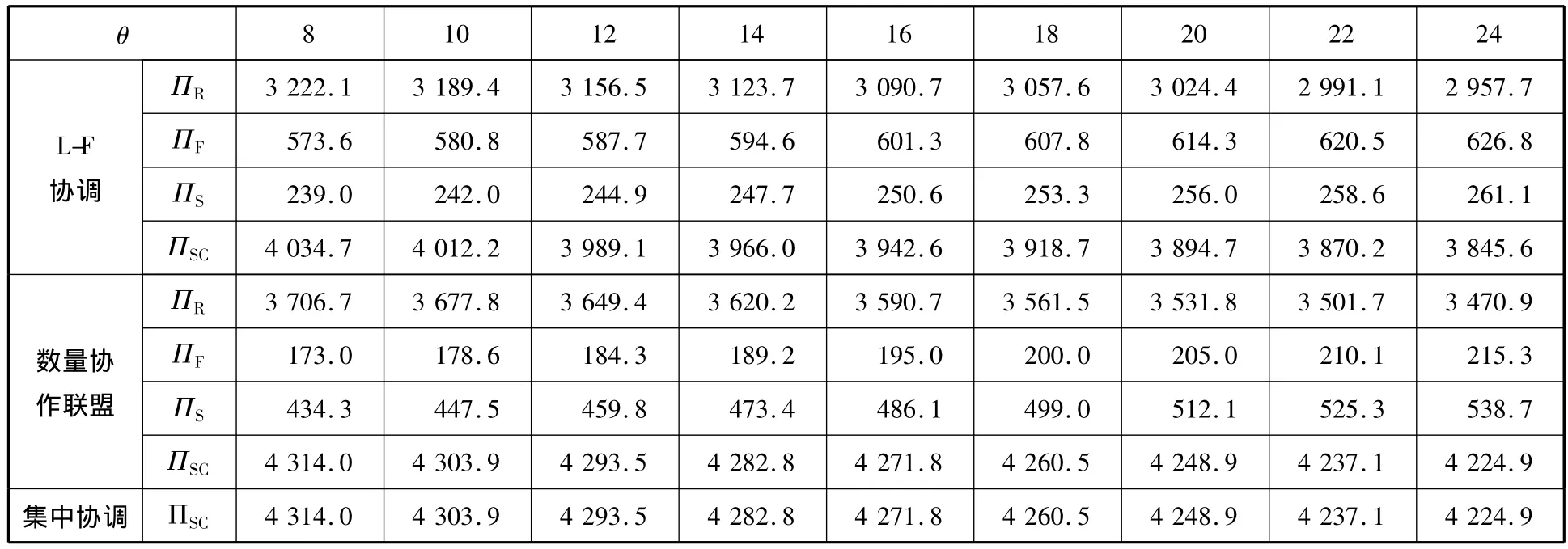
表4 θ对不同协调模式下供应链绩效的影响

表5 θ对不同协调模式下物流服务供应链各成员最优价格的影响

表6 eS对不同协调模式下供应链绩效的影响

表7 cS对不同协调模式下供应链绩效的影响

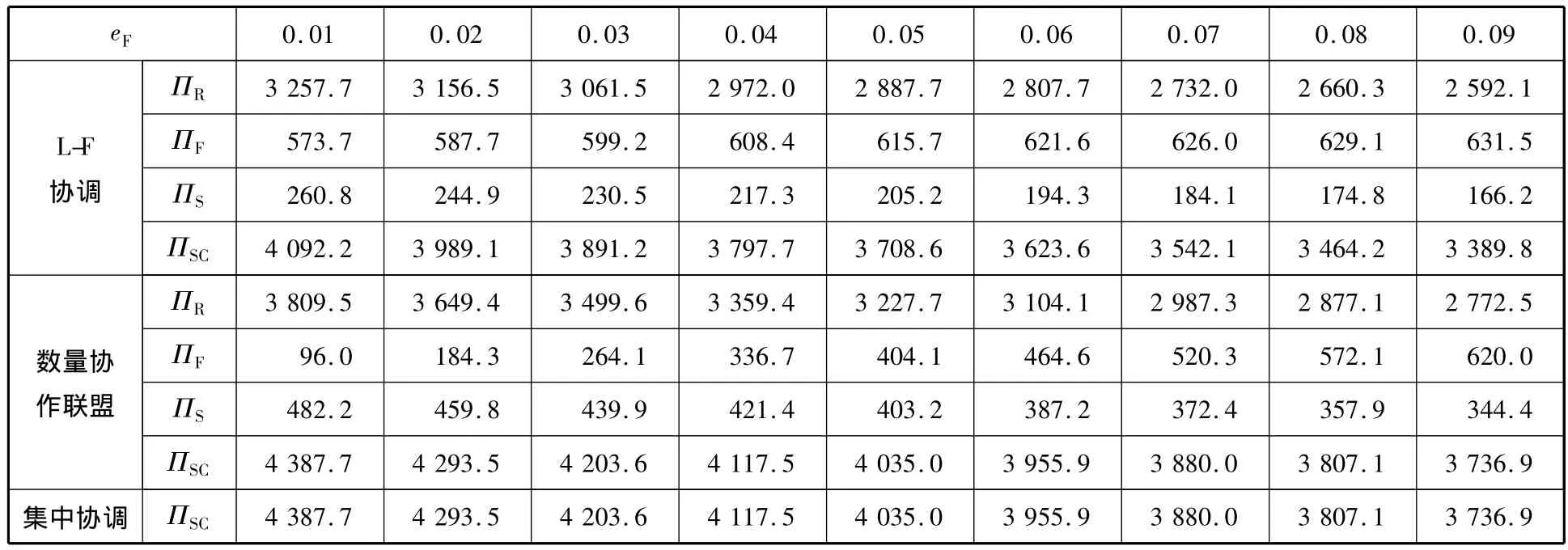
表8 eF对不同协调模式下供应链绩效的影响

(3)根据表 2，4，6 ～8 的数值结果，无论 k，θ以及各项物流能力成本参数如何变动，数量协作联盟均可获得集中协调模式下系统最优绩效，说明数量协作联盟是物流服务供应链分散决策下优良的协调模式.在该模式中，供应链各成员通过相互协商，可使物流能力数量的需求与供给最终达成一致，从而保证最优的系统绩效.这种数量协作联盟协调机制与著名的 Vickery－Clarke－Groves机制的协调方法相类似.

(4)根据表6～8的分析，3种协调模式的数值结果均显示:随着F和S成本参数值的增加，整个服务供应链绩效都降低;但随着S成本的增加，其期望利润增加;同样，随着F成本的增加，其利润也相应增加，但整体供应链期望利润下降.这说明随着整个物流服务供应链上游基础物流能力成本的增加，基础能力提供商的期望利润有所提高，但由于R同时面对上游基础能力成本的增加和下游市场不确定性的双重影响，其期望利润下降比较明显，最终导致整个供应链期望利润降低，上游提供商基础物流能力成本的变化对整体供应链绩效影响显著.

(5)各种情况下数量协作联盟的协调效果均优于L－F协调，并且可以取得集中协调模式下的期望利润水平，是一种较好的三级物流服务供应链协调模式，本文证明该模式的可行性，可以在实际中得到进一步应用.此外，数值实验也显示，数量协作联盟在实现系统绩效提高的同时，供应链内部各节点企业利润的增加并不一致，S增加最多，R次之，而F出现下降.因此，对于新增利润必须引入有效的再分配机制，以确保在满足个体理性约束的基础上，各成员企业的收益不小于L－F协调模式下各自的收益.同时，对新增利润的分配需要进一步考虑各成员企业在供应链中的地位及其谈判能力，这也是保证数量协作联盟有效实施的重要条件.

4 结束语

研究由物流服务集成商，功能型物流服务提供商和物流能力分包商组成的三级物流服务供应链的协调问题.对整体物流服务供应链的运作模式和不同协调方式下各供应链成员取得最优绩效的条件进行分析，证明数量协作联盟的可操作性和有效性.通过大量的数值分析对比市场不确定因素和各种成本因素对不同协调方式的影响，分析结果表明:市场不确定性因素都会导致3种协调方式下的整体供应链绩效的降低;上游基础物流能力成本的变化对整体供应链绩效影响显著;不同情况下数量协作联盟对三级物流服务供应链的协调均能够取得集中协调模式下的期望绩效，在实际应用中具有可操作性，是比较理想的协调方式.下一步的研究可以拓展到其他不确定需求情况，以及考虑功能型物流服务提供商和物流能力分包商都存在能力不足等相关问题.

［1］刘伟华，季建华.服务供应链:供应链研究新趋势［M］.北京:中国物资出版社，2006:2－3.

［2］KIRSTIN Z.Supply chain coordination with uncertain just－in－time delivery［J］.Int J Production Econ，2002，77(1):1－15.

［3］黄小原.供应链模型与优化［M］.北京:科学出版社，2004.

［4］孙荣庭，孙林岩，李刚.不确定需求下多零售商竞争的供应链协调研究［J］.工业工程与管理，2010(2):49－58.

［5］BERNSTEIN F，FEDERGRUEN A.Decentralized supply chains with competing retailers under demand uncertainty［J］.Manage Sci，2005，51(1):18－29.

［6］CHEN Kebing，XIAO Tiaojun.Demand disruption and coordination of the supply chain with a dominant retailer［J］.Eur J Operational Res，2009，197(1):225－234.

［7］马士华，王福寿.时间价格敏感型需求下的供应链决策模式研究［J］.中国管理科学，2006(3):13－19.

［8］HSIEH Chung－Chi，WU Cheng－Han.Capacity allocation，ordering and pricing decisions in a supply chain with demand and supply uncertainties［J］.Eur J Operational Res，2008，184(2):667－684.

［9］刘伟华，季建华，包兴，等.物流服务供应链两级能力合作的协调研究［J］.武汉理工大学学报，2008，30(2):149－152.

［10］YAN H，LIU K，HSU A.Optimal two－stage ordering policy with Bayesian information updating［J］.Production ＆ Operations Manage，2006，12(1):30－45.

［11］CHOI T－M，LI D，YAN H.Optimal two－stage ordering policy with Bayesian information updating［J］.J Operation Res Soc，2003，54:846－859.

［12］桂云苗.需求不确定下物流服务供应链协调［J］.计算机集成制造系统.2009，15(12):2412－2438.

［13］王晓立，马士华.供应和需求不确定条件下物流服务供应链能力协调研究［J］.运筹与管理，2010，20(2):44－49.

［14］崔爱平，刘伟.服务物流供应链中基于期权契约的能力协调［J］.中国管理科学，2009，17(2):59－65.

［15］崔爱平，刘伟.基于能力分工与合作的LSSC协调［J］.上海海事大学学报，2008，29(2):43－47.

［16］刘伟华.三级物流服务供应链最优收益共享系数确定方法［J］.西南交通大学学报，2010，45(5):811－816.

［17］DEMIRKAN H.The risk and information sharing of application services supply chain［J］.Eur J Operational Res，2008，187(3):765－784.