高负荷风扇级环境下叶片反问题设计

曹志鹏，尹红顺，夏 天，黄雄武，张 旭

(中国燃气涡轮研究院，四川 成都 610500)

1 引言

叶片反问题设计技术是实现风扇高效、高负荷的一种新技术手段。叶片三维反问题设计有两项关键技术：一是反问题设计方法，二是目标压力载荷选取规律。

风扇/压气机叶片三维反问题设计方法主要分为两类。一类是直接解法，根据给定的叶片表面压力分布求解无粘欧拉方程来直接修改叶型，粘性效应通过彻体力及壁面函数计算的剪切力来考虑。另一类是数值优化法，典型的有两种：一种是将优化目标定义为给定的叶片表面压力分布，采用三维粘性CFD与数值优化相结合的方式获得反问题解；另一种是三维/准三维耦合的反问题方法，即采用三维粘性CFD作为流场求解器，利用准三维方法(在S2面上求解周向平均流场)作为反问题求解器，耦合两者各自优点的迭代方法。三维/准三维耦合求解策略的优点在于：对于给定的叶片压力/速度环量或负荷分布，可改变叶片叶型、叶片积叠规律及流道获得反问题解，且计算量相对较小，工程适用性较好。

叶片反问题设计中的载荷分布与叶片通道内的流动参数(压力、速度等)直接相关，决定了叶片通道内的激波结构。与叶片正问题设计方法相比，反问题直接关注与损失相关的压力载荷分布，能合理组织激波结构，对高进口马赫数、高负荷的叶型设计适应能力更强。

本文基于叶片三维反问题设计思想，发展了适用于级环境下高负荷风扇的叶片反问题设计程序。以单级风扇设计为例，通过从基元截面、单排到单级环境逐步深入的方式，对反问题设计方法及设计软件进行了验证。单级风扇的三维数值模拟显示：利用反问题设计程序，通过调整基元截面的载荷分布得到反问题叶片，能较好地控制风扇转、静子激波结构，降低损失，提高效率。

2 三维反问题概述

2.1 设计方法

叶片三维反问题设计输入需要给定速度环量或压力载荷、叶片法向厚度和积叠线，使用B样条对压力载荷分布和叶片厚度分布进行调整。速度环量、压力载荷及压力分布是三种不同的流动特征参数给定方式，一旦给定其中一种，叶片几何也就确定，激波和三维压力场分布控制成为可能。叶片法向厚度不仅用于保证转子结构完整性，还使设计者更为方便地考虑叶片结构和制造工艺的限制。求解欧拉运动方程采用有限体积法，时间推进采用四阶龙格-库塔法，粘性效应由彻体力和壁面函数计算的剪切力来计入。使用多重网格计算技术来增加稳定性和减少计算时间。反问题设计循环分为五步：第一步，在分析模式下完成初始叶片的流场求解，检查法向通量；第二步，选取基元截面，对载荷分布、厚度分布及子午型线等输入进行修改；第三步，在反问题模式下求解修改输入后对应的叶片几何；第四步，在分析模式中对比新叶片载荷与目标载荷；第五步，运用N-S方程对新设计叶片进行分析[1～6]。

2.2 压力载荷分布

直接控制叶片载荷可改变三维激波结构、二次流动和顶部间隙涡[7]。在相同进口马赫数下，控制叶片载荷加载规律可得到多道斜激波结构，能减少激波引起的损失。已有实例的压力载荷分布的基本规律是：转子叶片尖部为后加载叶型，采用正攻角；根部为前加载叶型，使用负攻角。

3 级环境下的叶片设计方法

基于上述叶片三维反问题设计思想，发展了级环境下叶片三维反问题设计程序。程序核心部分(二维基元叶型反问题设计程序[8～10]及三维粘性计算程序[11，12])由北航宁方飞教授开发。在主程序基础上，为与压气机设计体系的叶型设计程序对接，本文完成了数据转换接口程序及基元叶片积叠程序开发。

单级风扇三维反问题设计循环分为四步：第一步，三维粘性流动分析，确定需要改进的转、静子基元截面；第二步，根据设计目标修改基元截面的载荷分析；第三步，单排叶片反问题设计；第四步，级环境下的三维粘性流动模拟，分析性能改善效果。重复上述步骤，直至达到设计目标。通过上述四步，从基元截面、单排到单级环境逐步深入的方式，进行单级风扇的反问题设计与验证(见图1)。

基元截面叶型反问题设计是三维反问题设计的关键，具体步骤是：在原风扇转、静子三维叶片中选取需要改进的基元截面，利用本文开发的数据转换接口程序，将流线面叶型数据转换为基元平面叶型数据，同时确定流管厚度；利用宁方飞教授开发的S1流面正问题计算程序对基元平面叶型进行初步流动分析，得到初始叶型表面压力分布，结合三维流动结果对压力分布进行分析和调整，确定目标压力分布曲线；输入目标压力分布，利用叶型反问题程序迭代计算，直至得到与目标压力分布基本一致的叶型。至此，基元平面叶型反问题设计完成。

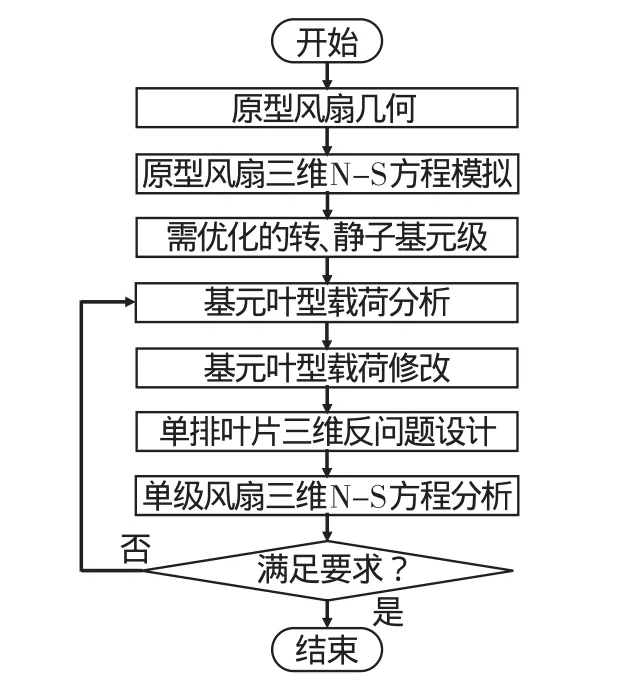
图1 级环境下叶片反问题设计流程Fig.1 Flow chart of airfoil inverse method design in stage environments

4 单级风扇三维反问题设计

叶片三维反问题设计对象为一高负荷单级风扇，级压比达2.1，进口轮毂比0.33，进口叶尖相对马赫数达1.73。

4.1 三维粘性流动分析

为验证三维反问题方法的有效性，利用发展的叶片反问题设计程序，选取高负荷单级风扇作为反问题设计对象，进行级环境下的叶片反问题设计。从子午掠形上可看出，单级风扇负荷很高，为避免转子叶片出现强度、振动问题，叶片尖部的子午弦长较短，这增大了气动设计难度。因此采用叶片三维反问题方法对原单级风扇转、静子叶片进行改进设计，通过新设计手段来改善风扇的气动性能。

为确定转、静子需要改进的基元截面，首先对高负荷单级风扇进行三维数值模拟。从三维流动求解结果(图2)看，原单级风扇在A、B、C三个区域中存在一定的流动分离，由此带来的损失会影响风扇效率。在转子尖部区域A，激波前的马赫数达1.60，强激波后尖部气流明显减速，逆压梯度增大，激波附面层的相互干扰及转子顶部间隙流动的影响，使得区域A中的流动损失较大。转子根部前缘区域B，由于转子前缘子午面掠形设计，使气流在该区域形成一较大的正攻角，引起气流分离。静子根部前缘区域C，由于静子的进口绝对马赫数较高，激波前的马赫数达1.42，正激波后绝对速度降低较多，因此存在明显的流动分离。根据上述分析结果，选定风扇转子叶片70%叶高以上的5个基元截面和静子40%叶高以下的7个基元截面进行反问题设计。

图2 原型风扇子午面相对马赫数(转、静子吸力面)Fig.2 The relative Mach number distribution of the origin fan blade meridional plane(suction surface of rotor and stator)

4.2 基元截面载荷分析

转子尖部5个截面的进口马赫数较高，流动损失较大，因此同时调整5个基元截面载荷，并保持各个截面压力载荷在径向上光滑过渡。为提高稳定裕度，以后加载为压力载荷调整方向，同时光滑吸、压力面上载荷以降低损失。

由于单级风扇的负荷高，使得静子根部区域的负荷较大，且越靠近静子根部，气动负荷越大，流动控制越困难。尤其是叶片前缘，吸、压力面上静压分布不光滑，引起总压损失较大。与转子一样，同时调整静子7个基元截面载荷，并保持各个截面载荷光滑过渡。静子根部都采用前加载叶型，将静压分布调节得较为光滑，有助于降低损失，提高静子的总压恢复系数；调整载荷分布，降低激波引起的逆压梯度，激波由一道变为两道，激波强度降低，引起的损失相应下降。从基元截面调整结果上看，越靠近静子中部，基元叶型反问题带来的性能提高越少，靠近静子根部处的改进效果较好。

反问题设计的最终叶型表面压力分布，与给定的目标压力分布存在一定差别，如静子吸力面上静压载荷前移不够，未完全达到给定目标压力分布的预期值。原因为：基元平面上的反问题叶型求解受安装角等约束条件限制；叶型的压力载荷分布没有经验值可供选取，由人为直接给定，具有一定的任意性。目标压力分布如果不合理，就不能得到有效叶型，这种情况下反问题得到的叶型是最接近目标压力分布的叶型。合理的目标压力分布是叶片反问题设计中一个十分重要的问题，目前对载荷分布规律的研究还处于初步探索阶段，没有成熟的选取经验。

4.3 单排叶片反问题设计

将转子叶片70%叶高以上5个基元截面调整后的压力载荷作为输入，同时引入最大厚度及积叠线约束，利用反问题设计方法进行转子叶片设计，得到三维转子叶片[13]。对单级风扇转子进行三维粘性流动模拟，对比90%叶高处反问题设计转子与原型转子的流场结构可得出：反问题设计后的转子正激波向转子出口移动，叶片吸力面上分离点向尾缘移动，分离区域减小，三维流动结构基本反映出5个基元截面载荷的调整效果。

同转子一样，将静子叶片40%叶高以下7个基元截面调整后的压力载荷作为输入，同时引入最大厚度及积叠线约束，利用反问题设计方法进行静子叶片设计，得到三维静子叶片。

4.4 级环境下的流动分析

完成单排叶片反问题设计验证后，进行单级环境下的流动分析，评估由三维反问题设计的风扇叶片在级环境下的性能改善效果。

利用三维粘性方法对反问题设计的单级风扇进行数值模拟，保持网格拓扑结构及求解参数等设置与原型风扇的完全一致，所得反问题设计风扇子午面相对马赫数分布如图3所示，90%叶高处拟S1流面相对马赫数分布如图4所示。对比图2、图3可看出：利用反问题改进设计后，A、B、C三个区域的流动分离明显改善。在转子尖部区域A中，虽然波前马赫数变化较小，但激波发生了一定程度的倾斜，激波强度减弱，激波前后马赫数变化减小，低速分离区显著缩小，损失降低。在转子尖部流动得到改善的同时，整个转子的流通能力得到加强，转子的轴向气流速度增大，因此在区域B中，由于转子根部前掠引起的正攻角减小，流动分离得到改善。静子根部附近由于激波、附面层干扰引起的流动分离随着叶型的改进得到了有效控制，低速流明显减弱，有助于提高静叶根部的总压恢复系数。

从图4中可看出：反问题设计后转子正激波向出口移动，激波后的马赫数升高，激波强度降低；吸力面上分离区没有完全消除，但分离区减小，分离点向尾缘移动，与基元截面、单级风扇转子的流动改进方向一致。这表明对叶片局部区域进行反问题设计，能改善单级风扇的性能。

30%叶高处拟S1流面相对马赫数分布如图5所示。从图中可看出：原型风扇静子叶片在30%叶高处，由于激波、附面层相互干扰引起了静子吸力面上的流动分离，在对静子叶片分离处附近的7个基元截面进行反问题改进设计后，分离区基本消除，激波后的流动得到明显改善。

图5 S1面相对马赫数(30%叶高)Fig.5 S1 surface relative Mach number distribution(at 30%span)

4.4.1 压力载荷分析

调整转子尖部各基元截面压力载荷，一是消除由激波引起的压力分布不光滑，减小激波损失；二是尽量将激波位置后移，以提高转子尖部区域的稳定裕度。90%叶高风扇转子压力载荷对比见图6，可见三维反问题设计的叶片压力分布有一定后移，说明在反问题设计前后，级环境下的转子载荷分布变化趋势与基元截面的载荷分布调整方向一致。

图6 风扇转子三维反问题压力载荷分布对比(90%叶高)Fig.6 Comparison of rotor surface pressure loading distribution(at 90%span)

在静子根部基元截面中，压力载荷调整方向是将原静子叶型的高马赫数区域削弱，使其由一道强激波变为两道弱激波，以减少激波损失，提高总压恢复系数。20%叶高风扇静子压力载荷对比如图7所示，从图中可看出，在相应叶高处，三维反问题设计静子形成了两道激波，激波强度有一定减弱。与转子一样，反问题设计前后，级环境下的静子载荷分布变化趋势与基元截面的载荷分布调整方向一致。

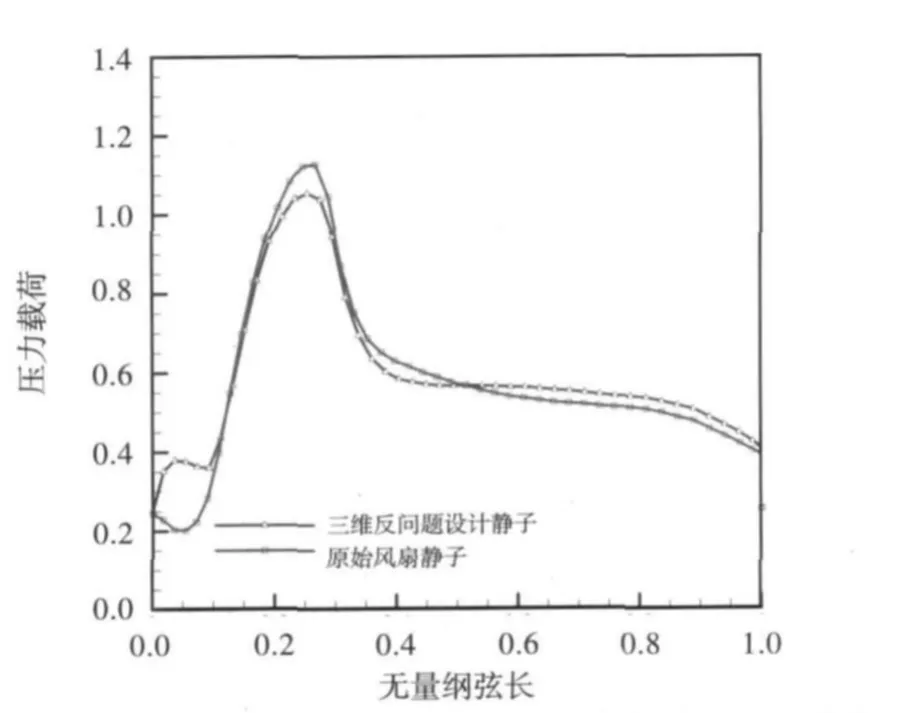
图7 风扇静子三维反问题压力载荷分布对比(20%叶高)Fig.7 Comparison of stator surface pressure loading distribution(at 20%span)

4.4.2 特性分析

原型风扇和三维反问题设计风扇特性对比如图8、图9所示。从图中可看出，相同背压下，反问题设计风扇流量增大，压比与原型风扇基本相同，效率提高；在近喘点，反问题设计风扇压比、效率都有提高，稳定裕度由原型风扇的11.1%提高到11.9%。

4.4.3 展向分布分析

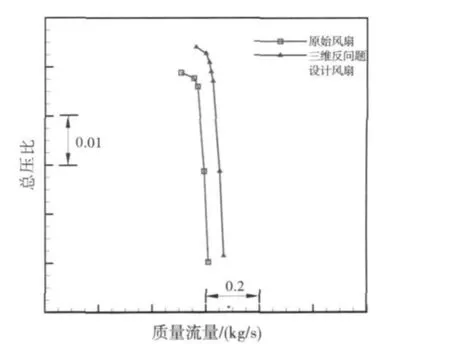
图8 单级风扇流量-压比特性对比Fig.8 Mass flow vs.pressure ratio of single-stage fan

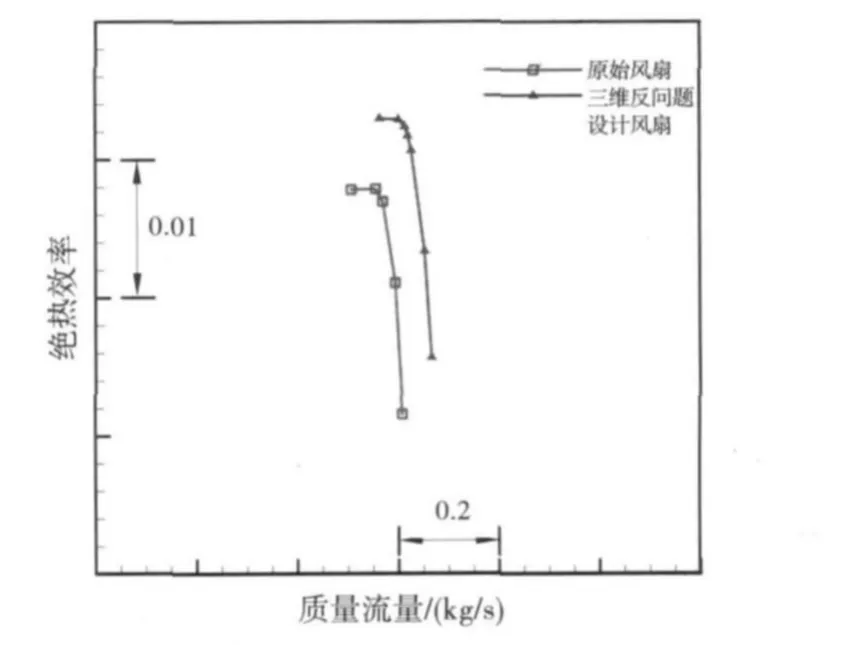
图9 单级风扇流量-效率特性对比Fig.9 Mass flow vs.efficiency of single-stage fan

反问题设计风扇转子效率展向分布见图10，图中显示，风扇叶片85%叶高以上的效率有一定提高。受转子效率提高的影响，静子相应叶高处的总压恢复系数也有一定升高(图11)。同时，由于静子叶片40%叶高以下截面经反问题改进设计后，局部流动分离减弱，因此总压恢复系数明显升高。通过对风扇转子尖部、静子根部叶型进行反问题设计，尖部和根部区域的效率升高，且效率分布更为均匀。上述结果表明，本文发展的三维叶片反问题程序及反问题设计方法，能有效提高风扇效率和稳定裕度。采用调整叶片局部载荷分布的方法，能改善三维叶片性能，有较好的工程实用性。

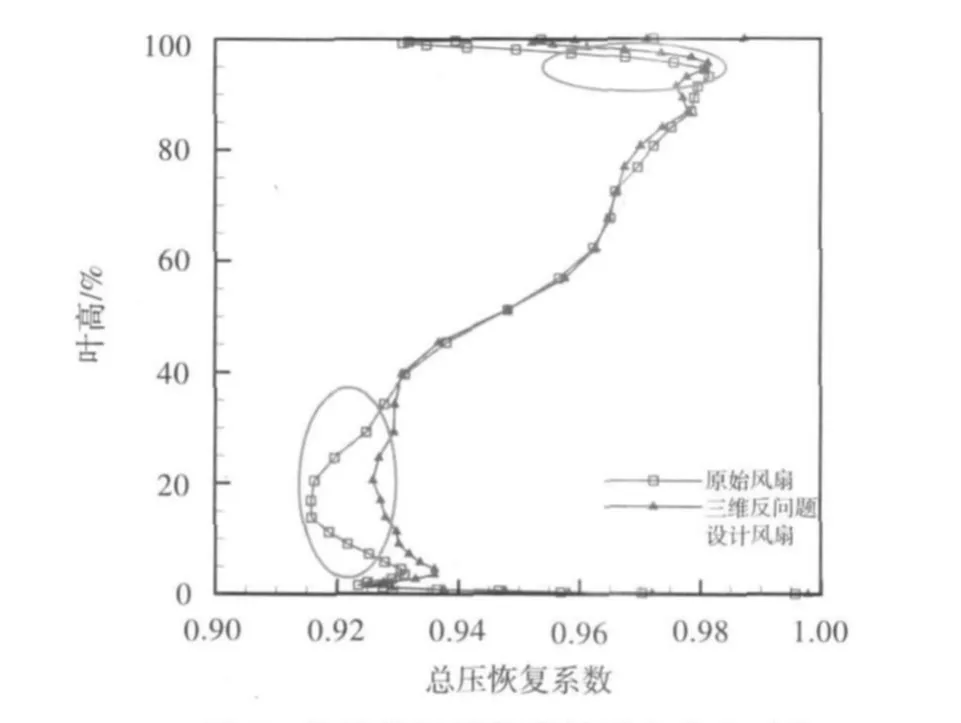
图11 静子总压恢复系数展向分布对比Fig.11 Comparison of stator total pressure recovery coefficient along the spanwise

5 结论

(1)目前叶片三维反问题主流设计方法，都是以叶片载荷展向分布为输入，同时考虑叶片厚度和积叠线的展向分布约束，通过三维反问题直接得到三维叶片几何，对新叶片几何进行粘性流动分析，不断修改叶片载荷分布，直到满足设计目标为止。

(2)基于级环境下的三维反问题叶片设计思路：以基元截面的吸、压力面载荷为输入，考虑叶片最大厚度、安装角、积叠线等约束条件，通过吸、压力面载荷分布调整，反问题设计和级环境下的三维流动分析等设计循环，得到满足要求的风扇叶片。

(3)以高压比单级风扇为例，通过基元截面、单排及单级环境逐步深入的设计分析，验证了级环境下三维反问题设计方法的有效性，初步探索了高负荷风扇叶片压力载荷选取规律，为工程应用奠定了良好基础。

(4)在众多设计约束条件下，反问题设计方法能有效提高叶片性能，但提高幅度较小，离工程应用还有不小差距。通过进一步深入研究，放宽限制条件，如安装角变化范围、积叠线空间形式等，叶片载荷分布规律会更加合理，高负荷风扇性能还能得到进一步改善和提高。

[1]Peixin H，Zangeneh M.On Design of Transonic Fan Ro⁃tors by 3D Inverse Design Method[R]. ASME GT2006-91173，2006.

[2]Medd A J，Dang T Q，Larosiliere L M.3D Inverse Design Loading Strategy for Transonic Axial Compressor Blading[R].ASME GT2003-38501，2003.

[3]Van Rooij M P C，Dang T Q，Larosiliere L M.Enhanced Blade Row Matching Capabilities via 3D Multistage In⁃verse Design and Pressure Loading Manager[R].ASME GT2008-50539，2008.

[4]Watanabe H，Zangeneh M.Design of the Blade Geometry of Swept Transonic Fans by 3D Inverse Design[R].ASME GT2003-38770，2003.

[5]Mileshin V I，Oreskhov I K，Shchipin S K，et al.3D In⁃verse Design of Transonic Fan Rotors Efficient for a Wide Range of RPM[R].ASME GT2007-27817，2007.

[6]Mileshin V I，Orekhov I K，Fateyev V A，et al.Effect of Tip Clearance on Flow Structure and Integral Performanc⁃es of Six-Stage HPC[R].ISABE 2007-1179，2007.

[7]Bonaiuti D，Pitigala A，Zangeneh M，et al.Redesign of a Transonic Compressor Rotor by Means of a Three Dimen⁃sional Inverse Design Method：A Parametric Study[R].ASME GT2007-27486，2007.

[8]杜 磊，宁方飞.基于控制理论的压气机叶型数值优化方法[J].航空学报，2009，24(3)：615—625.

[9]Blazek J.Computational Fluid Dynamics：Principles and Applications[M].Net Herlands：Elsevier Science，2001.

[10]Jameson A.Optimum Aerodynamic Design Using CFD and Control Theory[R].AIAA 95-1729，1995.

[11]Ning F F，Xu L P.Numerical Investigation of Transonic Compressor Rotor Flow Using an Implicit 3D Flow Solver with One-Equation Spalart-Allmaras Turbulence Model[R].ASME 2001-GT-0359，2001.

[12]Abu-Ghannam B J，Shaw R.Natural Transition of Bound⁃ary Layers-The Effect of Turbulence,Pressure Gradient and Flow History[J].Journal of Mechanical Engineering and Science，1980，22(5)：213—228.

[13]曹志鹏，兰发祥，夏 天，等.高负荷风扇转子叶片反问题设计[J].燃气涡轮试验与研究，2012，25(2)：1-6.