数学“再创造”提问价值的实践探索

课堂提问是初中数学课堂的必要环节，《课程标准》明确指出：数学课堂教学必须关注学生的主体参与，师生互动进行。而课堂提问是促进学生主动学习的有效方法之一。本文在总结数学课堂提问状况的基础上，对数学教学在回溯旧知、解决难点和教学反思中发挥“再创造”提问价值进行了阐述，希望能够为学生提供“再创造”机会，激励学生进行“再创造”活动，从而提高课堂效率。

一、数学课堂提问的现状

数学学习的本质是学生的“再创造”。在数学学习中，教师应给学生提供充分的“再创造”机会，激励学生进行“再创造”活动。因此在教学中，我们设计问题应尽量体现知识的“再创造”过程。

然而，目前的数学课堂提问还存在着诸多问题，归纳起来主要有三点。一是为“提问”而“提问”，用“提问”来代替教师的讲解，把“启发式教学”庸俗化成“问答式教学”，师生、生生之间并没有实质上的交流互动。二是所提的问题主要是记忆性的提问，往往是针对知识点就题发问，所提的问题缺乏深度、梯度和广度，缺乏适度的拓展、变式和延伸。三是忽视学生的年龄特征，提问偏题，随意性大，教师没去思考提问是否具有层次性、针对性和启发性以及提问想要达到什么样的教学目的，脱离了学生的“最近发展区”。

二、数学“再创造”提问价值的实施

“再创造”是一种教学思想，要求教学引导学生在实践活动中体验，像数学家一样去“发明”和“创造”。课堂上，教师要尽量多地为学生提供说、议、做、练的机会，让学生动口、动手、动脑，努力营造学生全面参与学习的浓厚氛围。同时，问题的设计应尽量体现知识的“再创造”过程。

第一，回溯旧知，发现新知。回溯就是将新知识还原到最初状态去，初始状态一是数学知识本身的“基本素材”状态；二是学生原有的认知经验和生活经验状态。教师通过提问将学生带回到原有的知识，“再”重新开始，可找准新知的“最近发展区”，然后教师再通过提问把学生带回到新知识本身，“创造”主动生成。

如在浙教版七下《相似变换》一课中如何让学生理解相似变换作圖是通过线段的扩大或缩小，而不是通过角度的扩大或缩小来完成的。笔者在教学中结合前一章《全等三角形》中全等三角形判定方法的探究来设计提问。

师：三个角对应相等两个三角形一定全等吗?

生：不一定全等(异口同声)。

师：为什么呢?

生：三个角对应相等，三角形的形状相同，大小不一定相等。

师：那么角度的大小是决定圖形的形状还是大小呢?

生：形状。

师：形状、大小相同的三角形才是全等的，那么必须加上关于什么的条件才能使两个三角形全等呢?

生：关于边的条件。

师：边的大小决定了圖形的什么呢?

生：圖形的大小。

通过这一系列的设问，学生从原有知识过渡到新知识，很自然地理解相似变换是通过线段的长度改变来实现的。

第二，设问启发，突破难点。数学教学倡导，让学生参与寻求解题思路的过程，体验分析解决问题的方法。由于知识结构和思维水平有限，学生思考问题往往有较大的局限性，而教师为了节约时间、完成教学任务，会直接告诉学生正确的解题思路和方法，导致学生的解题能力得不到提高。作为教师，应根据学生的“最近发展区”，抓住例题学习的核心，按照再创造的“层次性”要求，引导学生层层深入。这不仅是传道，而且是“解惑”。

如浙教版八年级下§6.4《梯形1》一课等腰梯形的性质引例：

已知：如圖，在梯形ABCD中，AD∥BC，AB=DC。求证：(1)∠ABC=∠DCB，∠BAD=∠CDA；

(2)AC=BD。

本例的知识核心是等腰梯形的性质证明；技能核心是通过添加辅助线把梯形的问题转化成平行四边形或三角形的问题，使学生体会圖形变换的方法和转化的思想。由于之前学生很少接触辅助线，因此这里要通过添加辅助线来解决问题有一定的难度，学生不知道如何根据题意，添加辅助线。这就要求教师从学生已有的知识水平出发，通过问题铺垫，适时适当启发，让学生亲身体验通过添加辅助线，将梯形问题转化为自己已有的知识进行解答。

某教师在课堂上的处理方法如下：

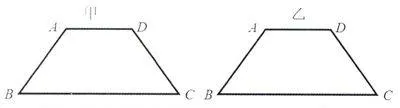
画一画：如圖，在梯形ABCD中，AD∥BC，AB=DC，你能把圖甲的梯形ABCD分成一个平行四边形和一个三角形吗?

你能把圖乙的梯形ABCD分成一个矩形和两个直角三角形吗?

请你任意选择一个圖形，并结合刚才的辅助线证明∠B=∠C。

完成教师设计的问题后，再呈现引例，学生就有了证明的思路。教师再适时地加以追问：你为什么要添加这样的辅助线?你把问题转化成什么问题了?通过师生互动，把完整的证明过程进行板演就水到渠成了。反思这位教师的教法，只是在教师讲解和学生思考之间搭建了合适的桥梁，给学生提供了“跳一跳，摘得到”的机会，但却达到了意想不到的效果。

第三，设问反思，提升能力。弗赖登塔尔说：“学习数学正确方法就是实行‘再创造’，学生本人把要学的东西自己去发现或创造出来。”数学中很多的概念、定理、公式需要学生通过实验、操作去发现，引导学生对操作过程进行反思，可以促进学生的“再创造”。

如教学浙教版七上《角和角的度量》一课，在探究角的概念时，教师进行了以下设计。

师：猜测过一点可以画多少条射线?

生(画一画验证猜测)：结论可以画无数条射线。

师：我们过一点画两条射线试试看是个什么圖形?

生(操作后发现)：是一个角。

师：角是我们已经认识过的圖形，请大家回忆，刚才这个角是怎么画出来的?

生(回想了一下)：过一点画两条射线。

学生反思后得出的结论和书上的结论几乎一致。在角的概念形成过程中，“反思”起了重要作用。没有对操作过程的反思，学生就难以用自己的语言说出角的形成过程、表述角的概念。

在数学解题中的反思也尤为重要。波利亚认为，在解题的四个环节中更为重要的是“解题回顾”。只有深刻反思题目中蕴涵的数学思想、方法，知识才能潜移默化地内化为能力，并在新情境中迁移。因此，教师要重视引导学生多方位、多角度去对例题进行联想、思考和探索，同时抓住时机，深化对问题的理解，培养学生的反思意识和习惯。如通过问“此题用到哪些基础知识?是否能把已知的条件转化为有效的解题思路和方法?解决本题的突破口在哪里?”来反思解题过程；通过问“这种方法是否更好?有没有更好?”来反思解题方法，帮助学生养成对数学方法归类、对规律小结和技巧揣摩的好习惯。通过问“你是怎么想的?为什么出错了?老师或其他同学是怎么想的?哪一种方法最优化?今后该如何思考此类问题?”来反思自己的学习错误。

如果学生在每次解题后都能对自己的思路作自我评价，并探讨成功的经验或失败的教训，那么学生的思维就会更加开阔，对新知识也能从更高层面进行概括。所以，教师在教学中要精心设置反思问题情境，有意创造反思机会，为学生学习和“再创造”提供机会。

作者单位浙江省杭州市余杭区太炎中学

(责任编辑 王胜霞)