控制论在保险精算中的应用

敬成林 韩爱华

摘 要:运用统计学习和反馈控制建立风险预测模型,是风险研究的新方法。利用控制论中的统计学习对小样本进行参数估计,结合反馈环节对建立的模型不断地进行修正,使模型越来越接近现实,形成连续的循环过程,最终逼近最优的风险模型,为保险公司的风险预测提供帮助。

关键词:控制论非寿险精算统计学习反馈

中图分类号:O231.5 文献标识码:A 文章编号:1674-098X(2012)07(c)-0189-01

1 国内外研究现状

精算内控系统的概念,最早源于英国精算师Jeremy Coford于1985年在the students Society杂志上发表的一篇关于寿险公司的金融控制的文章,这篇文章强调了英国寿险公司的整体精算控制方法的重要性,并指出精算是一整套系统的管理决策支持思想和方法[1～3]。2002年1月,澳大利亚精算学会提出了精算内控系统,并将精算内控系统解释为精算师的基本技能的应用。在我国保险公司的风险管理中,相当部分保险公司的风险评估还缺乏有效的评定标准,公司管理层及员工对关键性风险的认识和判断还不充分。2007年,西南财经大学的李恒琦等在精算内控系统理论分析一文中介绍了精算内控,但没有给出实际的风险模型,它是国内首篇定性介绍精算与控制相结合的文章。后来,研究人员认识到,通过模拟的方法,特别是Markov Chain Monte Carlo(MCMC)方法(Gilks et al,1996)的运用,完全贝叶斯分析所要求的计算可以由模拟方法有效地解决。实际上,只要保险业务量的数据足够大,完全可以在PC上通过多层贝叶斯(hierarchicalBayes)模型解决[4]。然而,实际数据采集中,我们往往得到的是有限的样本,这时,利用控制论中的统计学习和反馈环节对建立的模型不断地进行修正,使模型越来越接近现实,形成连续的循环过程,最终达到风险管理的目的。

2 保险精算中的控制理论

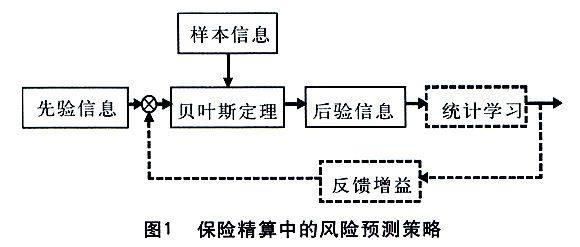
非寿险精算已经发展了两个重要分支:一是损失分布理论,研究在过去有限的统计资料的条件下未来损失的分布情况以及损失和赔款的相互关系等问题;二是风险理论,通过对损失频率和损失幅度分布的分析,研究这种出险次数和每次损失大小的复合随机过程,以其洞察保险公司应具备多大的基金,方可不“破产”,以及评估“破产”概率的大小等问题[5]。已有的研究是基于贝叶斯推断的基本方法,是将关于未知参数的先验信息与样本信息综合,再根据贝叶斯定理,得出后验信息,然后根据后验信息去推断未知参数(如图1实线部分),整个过程是个开环推断过程。主要是借助统计学习对小样本的预测功能,结合控制反馈思维构成如图1的闭环学习系统,对损失分布和风险模型参数进行统计学习控制,从而得到鲁棒性较强的最优参数估计,使得风险模型更精准,预测能力更强。

风险预测是风险管理的重要组成部分,它是风险规避即控制的基础。风险是可以预测的,从现代的概率论和数理统计可知,风险是一种损失的随机不确定性,对于群体来说,各种风险发生的概率、损失的大小及其波动性是可以大致计算出来的。风险的这些特征表明,在实际的保险经营中,不可避免地存在着一定的风险,同时这些风险又是可以通过科学的方法来预测和减少的。这就要求,在保险的经营中必须考虑到这些风险的存在,运用定量的方法进行精确的风险分析与预测。

图1所示的风险预测策略就是结合控制论的反馈思想和统计学习对小样本的预测能力,力求建立较精确的风险预测模型,为保险公司的财务运作提供技术支持,以便进行提前的风险管理和处置。我国在保险精算方面的研究相对滞后,风险预测研究有利于促进保险公司在精算方面的发展,提高保险业应对风险的能力,促进我国保险业的发展。

运用统计学习和反馈控制建立风险预测模型,是风险研究的创新点,这是一个全新的研究视角。基于数据的机器学习(统计学习)是现代智能技术中的重要方面,研究从观测数据(样本)出发寻找规律,利用这些规律对未来数据或无法观测的数据进行预测。利用统计学习对小样本进行参数估计,结合反馈环节对建立的模型不断地进行修正,使模型越来越接近现实,形成连续的循环过程,最终逼近最优的风险模型。为保险公司的风险预测提供技术支持。

3 结语

本文对控制论在保险精算中的应用作了一些介绍,控制论在保险精算中的应用很多,有许多应用还需要进一步地研究。在保险精算的研究中引入控制论的方法,使风险预测策略结合控制论的反馈思想和统计学习对小样本的预测能力,能够建立较精确的风险预测模型,从而为保险公司的财务运作提供帮助,

参考文献

[1] Clare Bellis,John Shepherd and Richard Lyon.Understanding Actuarial Management:the Actuarial control cycle[C],Southwood Press,2003.

[2] Dickson,D.C.M.L.M.Tedesco,and B.Zehnworth.Preidictive Aggregate Claim Distribution.The Journal of Risk and Insurance,1998,65:689～709.

[3] Bellis.Lessons from the Development of Regulation of General Insurance in Australia[J].Actuarial Communications,2002,3(2):78～85.

[4] 刘乐平,袁卫.现代Bayes方法在精算学中的应用及展望[J].统计研究,2002(8):45-49.

[5] 谢志刚,韩天雄.风险理论与非寿险精算[M].天津:南开大学出版社,2000.