拓扑空间童话记(下)
孙立群
(接上期)
只有一个国王的星球
小王子握住我的手,在我的头上摸了一下,我整个身体就缩小了,只有他的小姆指那样大,他就把我放进他的上衣口袋,于是我们从窗口飞出,直上云霄。
我实在好奇,想要知道外面是什么样子。我把头从口袋中伸出,只见到处都是美丽的星星,那银河像是由钻石缀满的项链,高挂在天幕上。
我们来到一个小星球,那上面到处都是美丽的公园,公园里有许多国王和王后的雕塑像。我们进入皇宫,小王子把我介绍给了国王。
我对国王说:“至高尊贵的国王,在我所生活的地球上有一个著名的戏剧家,他的名字叫莎士比亚。他曾经这么说:‘我可以局限在一个小房子里,而认为自己是无穷空间的国王。”
“每个人由于生活环境的限制,他所看到的和所理解的空间及事物往往不一样,主观看法不一样,对同一事物就会有不同的争论。”
“我的祖先最初视界不大,以为他们生活的地球表面是平的。有一天,有一个人要去南方,他的马车却往北跑,人们笑他是‘南辕北辙,一定不会到达目的地,其实很可能这个人早就知道地球是圆的,只要往北走就可以走到他所要去的南方。”
“是的,我们以前也以为我们的星球是平的。”国王对我说。
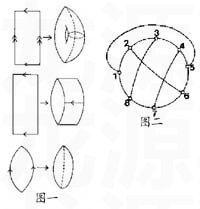
“这不奇怪。我现在剪下3块很薄的纸(见图一),我把它们的边缘黏起来。你可以看到3个不同的曲面。
第一个曲面像一个椭圆球,第二个曲面是圆柱,第三个是一个环面。我们现在可以看出它们是不一样的。假定我们生活在这些曲面上,而且我们的身体不断地缩小,小到平贴在表面上,我们在这表面上举目四望,就会觉得我们生活在一个平面上,而不知道它是椭球面、圆柱形面还是环面。”
“我同意你的说法,因为当我们变成渺小的生物之后,我们的眼睛只能看很小的一个范围,我们不知道我们生活的空间到底是什么样子。可是这和我的问题有什么关系呢?”
“国王陛下,在不同的条件下,一些事物可能有不同的发展和结果。在我的国家有一个传说:一个老人要把挡在他家门前的一座大山移走,他带领着全家老少每天去挖山,他认为每天挖一些,山不会增高,就算他在世时见不到山被移走,他的子子孙孙万代不竭地去挖这座山总会被挖走。
“可是如果我现在不是叫老人去移山,而是叫他移一条弧线,摆在他面前的是一个圆(如图二):
连结顶点2和顶点6的弧是会和连结顶点3,8及顶点4,7的弧相交。想象这些弧都是由橡皮圈做成的,我是否能把弧2和6适当移动,使它们保留在表面上又不与任何其他的弧相交?
我可以告诉您,这位老人再加上他的万代子孙是不能在平面上解决这个问题的,因为不管他们怎样移动,都没法完成我的要求。”
我说完了就站在一边,让国王和他的臣子们去讨论。争论了半个钟头之后,国王说:“我相信你的话,我们没法解决这样的问题。”
“现在你们经过各种尝试,得到经验,知道这问题是不能解决的,可是处在环状星球的人看到这个问题时会哈哈大笑,说:‘这是一个很简单的问题,我们的3岁孩子都能解决。因为他们的生活环境和我们的不一样,我们不能解决的问题,在他们那里很可能就变成可以解决的了。”
“你能不能告诉我他们是怎么解决的?我想知道结果。”
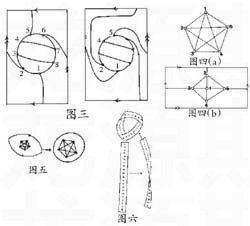
“好!现在我在这两张长方形的白纸上把刚才的图重画一遍。我先画顶点,然后画弧线(如图三),再把长方形的边相对黏合起来,这样我们的图就处在环面上了。顶点1和5及顶点2和6在这两个面上有不同的弧线连接,这些弧在环面上并不相交。”
小王子说:“也就是说,在平面上生活的人们不能解决的问题,在环状面生活的人却能解决。”
国王的问题的解决
“是的,你说得很对。我就是要说明一个很简单的道理:任何人处在不同的环境和不同的时间时,对一些事物的处理方式或了解就不一样。一些人看来简易的东西,对另外的人可能就是深奥的。一些看来是不能解决的问题,如果把立足点换一换,很可能就可以解决了。”
“那么为王子分配领土的问题是否可以解决?”国王焦急地问。
“国王,为王子分领土的问题可以这样看。如果把每个王子的领地用标有1,2,3,4,5的小圆圈来表示,如果两个领地有接壤,就用一个弧线连结起来。先看在平面上是否可以把任何一个顶点和其他顶点用弧相连且互不相交?我们的地球上有一位名叫库拉托斯基的数学家在50年代后就已证明这不可能。不管你怎样安排它们都会如图四(a)一样,总是有弧会相交,可是我却可以在环面上安排,使这些弧不相交,请您看图四(b)。
因此你们如果不想再对这问题伤脑筋,做不可能做的事,我可以提出一个卑微的建议:请你们移民到一个环状星球上去,这样你们的领土分配问题就可以解决了。”
“等一等!学数先生,你只说这问题在平面上不能解决,或许在圆球面上是可以解决的呢?”国王说。
这时我拿起笔在图四(a)上画了两条如图五左边的有箭头的弧线。然后拿剪刀沿着弧线剪,最后用浆糊把它黏起来,就像图五所表示那样:
“你看,我得到的是在圆球面上的图,它的顶点的相对位置不变,因此,在圆面上这问题仍然不能解决。”
“这真是奇妙的事,你能不能再告诉我一些关于曲面的新鲜事呢?”
只有一个面的扭带
看到国王的兴致这样高,我继续讲下去。
“请你们看我手上的长方形纸条,你们知道它有四个边、有两个面:如果我让纸条正对你们,你们可以说一个面是前面,另外一个面是后面;如果把纸条平放在桌上,你们可以说一个面是上面,另外一个面是下面。”
“如果我手上拿的是圆球或是一个玉环,你们也可以说他们有两个面,一个是里面,一个是外面。因此我们会以为所有的曲面都有两个面,对不对?”
大家都点点头。我把手上的纸条扭了一下,然后把头尾两端黏好,得到了如图六的曲面:
“现在你们可以看到,这个曲面只有一个边,你们如果不相信可以用手摸,它不像圆柱曲面有两个边,更巧妙的是,这个曲面只有一个面!”
国王摇摇头:“我看到的是两个面。”
“这是你的眼睛在欺骗你,固有的看法使你不容易接受事实。怎样证明圆柱形的面有两个呢?你会说很容易,我可以在一面上涂上红色,另外一面上涂上蓝色,这样就能明显地看出两个面来。好,现在请你用红色彩笔把这个扭带涂上颜色。”
涂上颜色之后,国王说:“唉呀!果然只有一个面,我现在得到一个全红的扭带!”
我拿着原先做好的圆柱纸圈,沿着中间平行两个边的大圆剪去,就得到了两个圆柱。
“你们能不能猜想:当用剪刀把这个只有一面的扭带顺着平行一边的纸条的中间剪下去,会得到多少个扭带?”
其他的人都异口同声地说:“两个!”
我把剪刀交给国王,国王以为可以分成两个扭带,实际上却没有剪开,得到的是一个更长的扭带。
国王目瞪口呆,喃喃自语:“这是怎么一回事?”
我又做了一个扭带,对国王说:“如果沿着纸条宽的三分之一的一个平行边剪,你会得到不同的结果。你们去试验和研究吧,我已经很疲倦了,我要回我的小房子做我的无穷空间国王梦了。再见了,国王和大臣!再见了,可爱天真的人们!”
于是我回到了地球……

