子四浪起点决定中期极值低点
大愚和尚

市场本周四个交易日维持低位震荡盘整格局。市场在19日和21日连续两天探底1995点后向上反弹拉起。预期市场在下周初将会有一个方向选择出来。且看是短期底点向上运行子四浪反弹亦或者是结束了子四浪反弹而开始向下进行最后子浪的下跌。
笔者在上周做客本栏目时曾经就极值底点可能出现的时间、空间和运行结构进行了一个预测分析。本周,我们再来回顾上周的观点。上周观点如下:
市场在19日前后运行子四浪向上反弹,运行时间约5个交易日,空间不过2053点;其后运行向下的子五浪杀跌,运行时间为10个或15个交易日,极限是20个交易日(运行时间为5的倍数);运行空间约到达1850点一线;其运行结构为五浪下跌模式。
在文章发表后,有热心读者通过博客联系笔者,提出最后的中期运行结构是否可能为一个特殊的终结形态,如终结三角形或下降楔形等。在此,笔者首先感谢读者朋友的交流互动,其次本周说明一个情况:上周的文章主要按常规出现的五浪下跌模式进行的结构划分,实际出现特殊的终结形态的可能也比较的大。常见的终结形态如:三角形、下降楔形等。
如果市场运行此类形态则子四浪反弹就有可能上碰一浪低点(2053点),所以子四浪反弹的上升可以上碰2053点一线,但不能突破2098点一线收盘,最高点更不能上破一浪起点2138点。
19日的1995.72点是否是子四浪反弹的起点?此为下周需要重点观察的一个地方。下周走势对应如下两种可能:
A:如上周所述19日(20日)即开始了子四浪反弹,如图一所示:
按此图运行则需要特别注意26日(27日)或12月3日(4日)处是否为相对高点向下的性质;在上周文章中笔者将子四浪反弹定性为弱势平台型反弹,如此成立,则有望于26日(27日)或12月3日(3日)处开始最后一个小级别子浪的下跌;
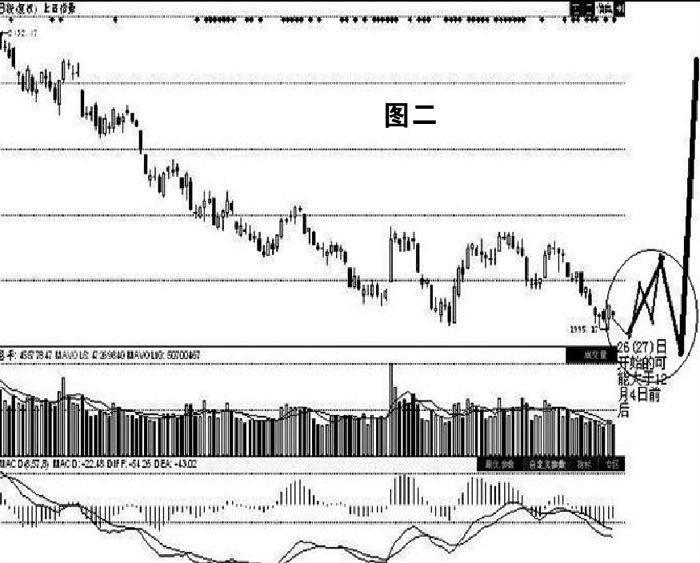
B:子四浪反弹并不是开始于11月19日,如图二所示:
按此图运行则市场会继续于11月23日一线向下突破,继续打破1995点的而创出新底后正式开始子四浪的反弹式上升。此时间笔者倾象于迟不过26日(27日),12月4日前后的时间离的有些远,各方面条件都不支持。
上面两幅短期运行走势图的细微差别之处在于19日是否开始了子四浪反弹,其将决定子五浪低点也即是中期低点将会于何时产生。如果按“图二”的走势,则中期极值低点在12月中旬前后难以出现,有可能产生的时间会到2013年的1月份去了。同时,读者朋友也需要注意,上面两幅走势运行图有两个共同点:
1)、市场中期极值底点出现前还会有一个子浪杀跌要运行,当前在结构上是不完整的;
2)、同时,根据前面分析,此处极值底点出现的空间都指向了1850点一线。
11月26日(27日)是一个根据短期参数计算出来的共振日线时间节点,虽然不如12月12日(或其后十个交易日)重要,但也不可小视。因为离此时间节点仅有一个交易日(23日),所以23日的突破方向显得极其重要,其将决定下周初的时间节点性质,同时也可以决定中期低点出现在2012年还是2013年。需要大家特别的关注!
2012年12月的日线时间节点为:
12月3日,12月5日,与11月15日所在周给出的12月4日产生共振,此处取124日前后一个交易日;
12月17日,12月19日,12月12日(或其后十个交易日的12月26日处)。
笔者在此强调两点:
第一,重要底部或等待出现极值低点或运行于结构最后一子浪部分时,应该以空间为主,时间为辅。因为时间节点或级别性质在不确定唯一性的情况下,空间的判断相对更简单更实用;当然了,除此之外的情况,则应该是时间为准、空间为辅。
第二,操作策略胜过一切,不要一味的深究细究于子浪运行或分时划浪,得不偿失,容易错而且相当费时费力。此处笔者只要明白:子四浪反弹完了还有最后一个子五浪的下跌,跌完后就会探出中期极值低点。至于笔者上面所描述的子四浪是否已经开始、何时结束等大可不必纠结于此。只要知道了结构还没有走完,大致的空间还没有到达和大致的时间还未到达就可以了!
操作策略:
笔者上周针对可能于19(20)日出现的子四浪反弹所给出的操作建议是继续空仓观望。本周,笔者给出的操作建议是据下周初的时间点性质而相机行事。
下周初出高点则继续空仓观望;下周初出短期低点则可以(仅可以)轻仓介入。本周和上周的操作策略不同,虽然都是针对的是子四浪反弹,但考虑到运行时间和反弹空间的不同而给出了不同的策略。19日开始的是弱势平台反弹,无参与必要;而26日(27日)开始的则可能是有一定空间和运行时间的四浪反弹,此处因为三浪运行时间的拉长而不能排除掉五浪是否是失败浪,同时也不能排除掉会走终结形态、此反弹会上碰一浪低点。所以时间不同,同样的子四浪反弹采取的操作策略也是不同的。

