分布式卫星SAR相位同步的实现方案及试验验证
李世强 禹卫东
(中国科学院电子学研究所航天微波遥感系统部 北京 100190)
1 引言
分布式卫星合成孔径雷达(SAR)系统由两颗或两颗以上的卫星构成,其中一颗卫星(主星)发射雷达信号并接收回波,其它卫星(辅星)只被动接收回波信号。分布式卫星SAR系统容易形成较长且稳定的基线,特别适用于高精度干涉SAR(InSAR)测高应用。
在分布式卫星InSAR系统中,主星和辅星成像后各自生成单视复图像,对两幅单视复图像进行相干处理,不同地形高度在干涉图中反映为不同的干涉相位,通过对干涉相位的分析可以获得地表的高程数据[1]。理想情况下要求干涉相位中仅包含地形高度引入的成份。实际上,由于主星与辅星各自采用不同的晶振,它们的回波信号中会存在由晶振频率偏差和相位噪声等引入的相位误差,因此,为了保证分布式卫星SAR系统的正常工作,需要解决卫星之间的相位同步问题。文献[2]讨论了分布式SAR对雷达基准频率信号相干性的特殊要求(不同于单站SAR),文献[3]讨论了频率源相位噪声在分布式SAR中引入相位误差的机理,并提出了分布式SAR相位同步方案的初步设想,在此基础上,文献[4]提出了用于TanDEM-X的相位同步实现方案,该方案在测量相位同步误差的过程中,采样频率远小于两颗卫星的雷达载波频率差,造成相位误差提取过程中出现模糊,增加了相位误差提取和补偿的难度。
本文提出了一种分布式卫星SAR相位同步的改进方案,采用基于GPS驯服晶振的双向对传相位同步脉冲的方案,经过GPS驯服后雷达载波频率差小于 1 Hz,使得相位误差测量过程中的采样满足Nyquist定理,可大大简化相位同步误差提取和补偿的复杂性,提高了相位同步的可靠性。本文在介绍相位同步实现方案的基础上,分析了影响相位同步性能的因素,讨论了相位同步工程实现需要解决的几个问题,通过地面试验验证了本文方案的性能。
2 相位同步实现方案
在分布式卫星SAR系统中,主星与辅星雷达载波的频率偏差和相位噪声将影响分布式 SAR成像以及干涉处理的性能,为了实现主星与辅星的相位同步,需要在主星与辅星之间建立一个共同的雷达载波相位参考,使得主星与辅星的雷达载波相位都与这一参考相位相同或接近。为此可以考虑在主星与辅星之间建立一个相位同步链路,通过对主星与辅星的雷达载波相位的双向对传,辅以相位补偿处理,可在成像处理前实现相位同步。
2.1 相位同步方案原理
在分布式卫星SAR中,造成主星与辅星相位同步误差的主要因素是雷达载波的频率偏差和相位噪声,从原理上来说,只要通过雷达载波的双向对传,获得主星与辅星的频率差和相位噪声信号(如图1所示),用它补偿辅星接收回波,即可实现相位同步。图中f1和f2分别为主星与辅星的雷达载波频率,Δf为主辅星频率差。
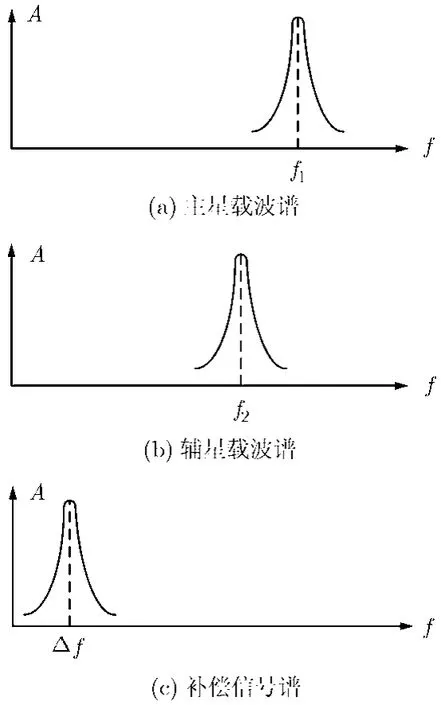
图1 主辅星载波谱及补偿信号谱
根据以上原理,Younis等人[5,6]提出了一种相位同步实现方案,用于TanDEM-X系统中,即在SAR工作过程中,双向对传相位同步信号,解调后随原始数据下传,地面处理时提取相位同步误差,补偿辅星回波实现相位同步。这种方案中主星与辅星雷达基准频率源各自独立采用高稳晶振,由于晶振频率准确度一般在 1 0-6量级,使得主星与辅星的X波段雷达载波频率差有可能接近20 kHz,远大于同步脉冲重复频率。而同步脉冲双向传输过程相当于是用同步脉冲重复频率fsyn对相位同步误差信号进行采样,使得相位误差提取比较复杂,需要实时测量主星与辅星的频率差,据此进行相位解模糊[7]。
本文在以上相位同步方案基础上,提出一种改进方案,即基于GPS驯服晶振的相位同步脉冲双向对传方案,同步方案要点如下:
(1)主星与辅星的基准频率源采用 GPS驯服晶振,由于 GPS卫星上采用的原子钟频率准确度在10-12量级以上[8],使得驯服后主星与辅星雷达载波频率差足够小。
(2)采用同步喇叭天线在主星与辅星之间交替传输相位同步脉冲信号,在同步脉冲传输过程中,正常的双站SAR数据录取被周期性打断,雷达发射信号从SAR主天线被切换到同步喇叭天线,主星发射的同步脉冲被辅星上的同步喇叭天线接收并采集,之后辅星经过适当延时再向主星发回一个同步脉冲信号,完成一个同步脉冲交互周期,如此循环往复直到成像结束。
(3)主星与辅星对各自接收的相位同步脉冲分别进行解调和数据采集,获得的同步脉冲数据通过数传系统下传地面,地面处理中提取相位同步误差,补偿辅星回波,完成相位同步。
相位同步过程中的时间关系如图 2所示。在t时刻,卫星1发射相位同步脉冲信号,经过传播延迟τ12后被卫星2接收。经过系统内部延迟τsys后卫星2在t+τsys时刻发射同步脉冲,经传播延迟τ21后被卫星1接收,以上过程在雷达开机时间内以同步脉冲重复频率fsyn反复进行。
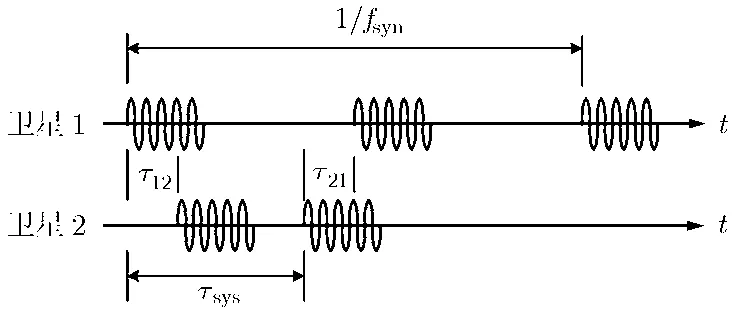
图2 相位同步的时间关系
[9]可知,同步脉冲重复频率一般可取为10 Hz左右,采用GPS驯服晶振后可保证主星与辅星的X波段雷达载波频率差小于1 Hz,从而使同步脉冲重复频率对相位误差的采样满足 Nyquist采样率,大大简化地面处理中相位同步误差的提取难度,这正是本文方案优于Younis等人方案的特征之一。
GPS驯服晶振将石英晶体振荡器优良的短期稳定特性和GPS信号良好的长期稳定特性结合起来,GPS驯服晶振的原理如图3所示。驯服电路实际上是一个锁相环,被驯晶振的输出经过分频整形后产生秒脉冲(PPS)信号,将其与 GPS接收机输出的PPS脉冲比相得到相位差,对该相位差进行数字滤波,并经D/A转换后得到误差电压,控制被驯晶振的压控端实现频率调整。
2.2 相位同步性能分析
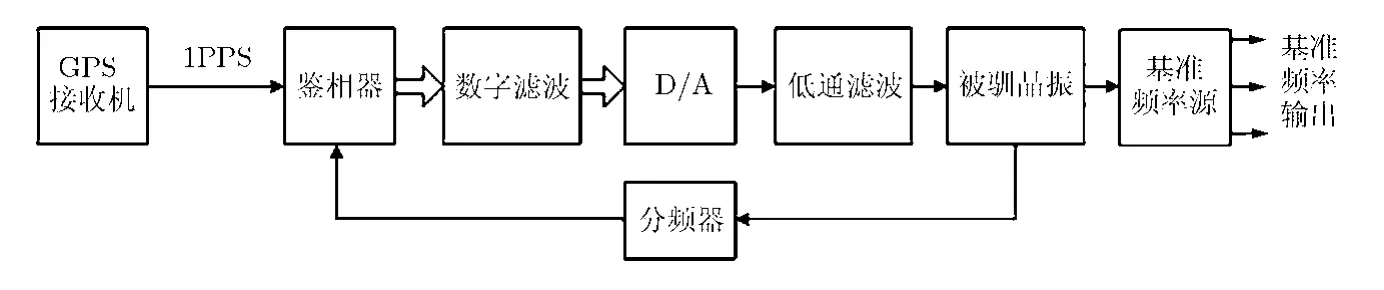
图3 GPS驯服晶振原理框图
根据前述相位同步实现方案,相位同步链路的硬件模型如图4所示。从图中可以看出,在相位同步脉冲传输过程中,造成相位变化的因素包括:发射和接收端的基准频率差Δfi,相位噪声nϕi,发射通道和接收通道的相位抖动ϕsysTi与ϕsysRi,同步喇叭天线相位方向图引入的相位变化ϕanti,接收机噪声引起的相位误差ϕSNRi,主星与辅星相对运动的多普勒效应引起的相位变化2πΔd/λ等,其中i=1或2分别代表主星或辅星。
若令主星与辅星的雷达载波频率为fi=f0+Δfi,其中f0为标称频率,Δfi为卫星i的频率偏差。则t时刻卫星i的雷达载波相位为

其中ϕ0i为卫星i的雷达载波初相,nϕi为载波相位噪声。

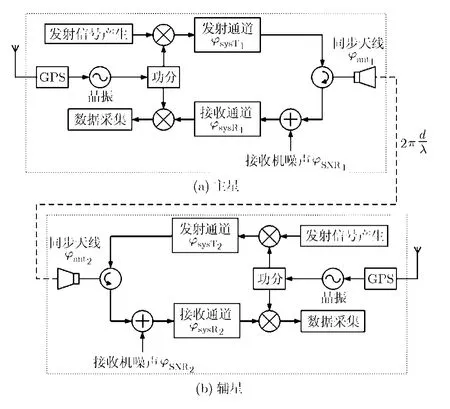
图4 相位同步链路的硬件模型
提取补偿相位的目的是获取主星与辅星频率偏差和相位噪声引起的相位同步误差,在此过程中引入的其它相位将成为影响相位同步性能的干扰相位。从式(2)中可知,第3项为主星与辅星频率偏差形成的相位差,第5, 6项是相位噪声形成的相位差,这些正是补偿辅星回波相位,实现相位同步需要的成分。其它项均是在双向同步脉冲传输过程中引入的额外相位误差,将形成相位同步后的剩余相位误差。其中第7项为接收机噪声引入的相位误差,第8, 9项为雷达收发通道相位抖动引入的相位误差,第10, 11项为一次相位同步脉冲对传过程中,主星与辅星相对位置发生变化而又同步喇叭天线方向图引入的相位误差,式(2)等号右边第1项为由卫星相对运动的多普勒效应引入的相位误差。
根据分析,同步天线方向图引入的相位误差远小于1°,可以忽略;根据工程经验,雷达收发通道的相位抖动一般可以控制在1°以内,对相位同步性能影响也较小[10];当卫星相对运动的速度稳定或变化不大时,多普勒效应引入的相位近似为常数,对相位同步性能影响较小,因此影响相位同步性能的主要因素将是接收机噪声。
2.3 相位同步方案的工程实现
在相位同步方案的工程化实现过程中,需要考虑以下几个问题,即相位同步脉冲定时的设计、同步脉冲的增益控制策略,以及同步脉冲的数据压缩考虑。
(1)相位同步脉冲的定时设计 在相位同步脉冲传输时,雷达信号需要从SAR天线切换到同步喇叭天线,为了给信号通路切换和天线状态切换留出足够的时间,需要同步脉冲发射时刻滞后于对地发射探测脉冲的时刻,同时控制数据采集起始的定时脉冲也与采集地面回波的时刻不同,因此需要定时信号周期性改变脉冲出现时刻。
(2)相位同步脉冲的增益控制 星载 SAR接收地面回波时,考虑到不同地物后向散射特性的不同,需要采取增益控制措施保证接收通道增益与回波信号电平匹配。相位同步脉冲传输时,由于主星与辅星相对距离和相对角度的变化,使得接收信号也会发生变化。考虑到雷达一次开机期间卫星之间距离变化不大,并且相位同步信号传输链路始终位于同步喇叭天线的3 dB波束宽度内,使得同步脉冲信号电平变化范围不大,因此可以采用固定增益实现同步脉冲的接收。
(3)相位同步脉冲的数据压缩 星载 SAR接收地面回波时,一般会对回波数据采用分块自适应量化(BAQ)算法进行压缩以降低数据率。BAQ是针对SAR原始数据零均值高斯分布的统计特性专门设计的压缩算法,对SAR原始数据的压缩性能较好。而相位同步脉冲在距离向只有一个脉冲的时间宽度,而且其幅度的统计特性与地面回波不同,因此不宜采用 BAQ压缩算法。考虑到同步脉冲传输时之需要采集一个脉冲宽度的数据,每个脉冲的数据量小于地面回波,因此可以考虑对相位同步脉冲不做数据压缩,直接下传。
3 相位同步性能验证
按照以上相位同步方案,研制了具有相位同步功能的主星与辅星的X波段雷达中央电子设备,开展了相位同步的地面验证试验。试验中首先测试了基于 GPS驯服晶振的主星与辅星射频基准频率的准确度,之后将两套中央电子设备之间的相位同步链路连接好,开展了相位同步性能的测试。
测量 GPS驯服晶振的频率准确度时,将 100 MHz的GPS驯服晶振信号通过中央电子设备的基准频率源倍频到射频基准频率9300 MHz,待GPS驯服晶振锁定并稳定一段时间后,利用频率计测量倍频后的信号频率,共获得5组测量数据,每组测量数据大约为半小时的测量结果,图5给出了各次测量结果的变化曲线,表1给出了5组测量结果的统计值,从表中可知,经过GPS驯服后,X波段的基准频率偏差小于1 Hz,这位相位同步误差的提取奠定了较好的基础。
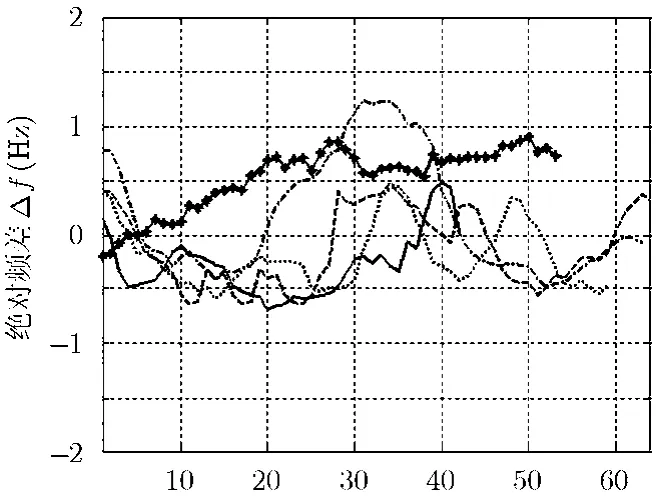
图5 X波段基准频率的测量结果
测试相位同步性能时需要的设备及其连接关系见图6所示。利用发射的LFM信号经过衰减后分别模拟回波信号和相位同步脉冲信号,对记录的雷达数据进行分析后可以获得相位同步性能:图7为主星和辅星回波相位历程,其中实线为主星回波相位历程,虚线为辅星回波相位历程。从图中可以看出,由于主星为自发自收工作,其相位基本不随时间变化,而辅星接收信号是由主星发出的,其相位随时间波动。从图8可看出,补偿相位的变化历程能够较准确地反映主辅星相位历程差的变化趋势;图 9给出了主辅星相位历程差与补偿相位历程的比较,以及利用补偿相位补偿辅星回波相位后剩余的相位同步误差,其中图9 (a)中实线为补偿相位,虚线为回波相位差,可以看出,补偿相位曲线与主辅星回波相位差曲线变化趋势非常接近,说明补偿相位可以较准确地补偿相位同步误差;图9(b)是相位补偿后的剩余相位同步误差,补偿后剩余的相位同步误差小于5.5°,可以满足分布式卫星SAR系统的需求。
4 结论
实现主星与辅星雷达信号的相位同步是分布式卫星SAR正常工作的前提之一,为了简化地面处理中相位同步误差提取和补偿的复杂度,本文提出了一种相位同步的改进方案,分析了影响相位同步性能的因素,讨论了工程实现时需要考虑的几个问题,最后通过地面试验验证了本文提出方案的性能。

表1 5组测量结果的统计值(Hz)
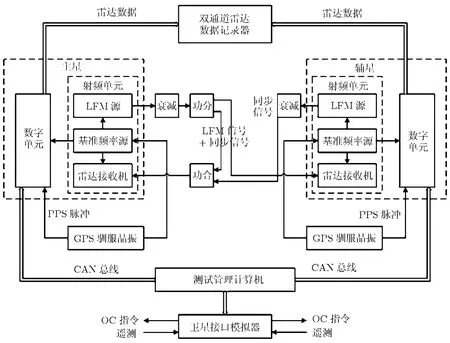
图6 相位同步性能测试框图
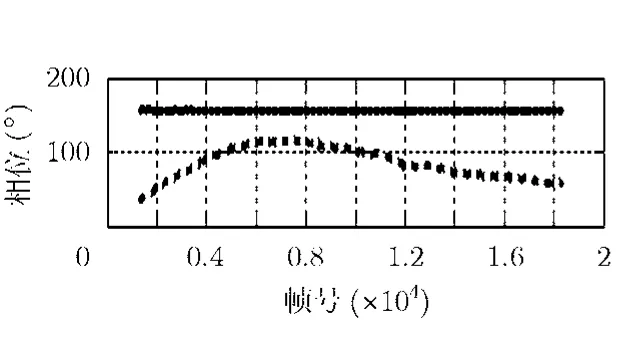
图7 主星和辅星回波相位历程

图8 主辅星回波相位差与补偿相位历程
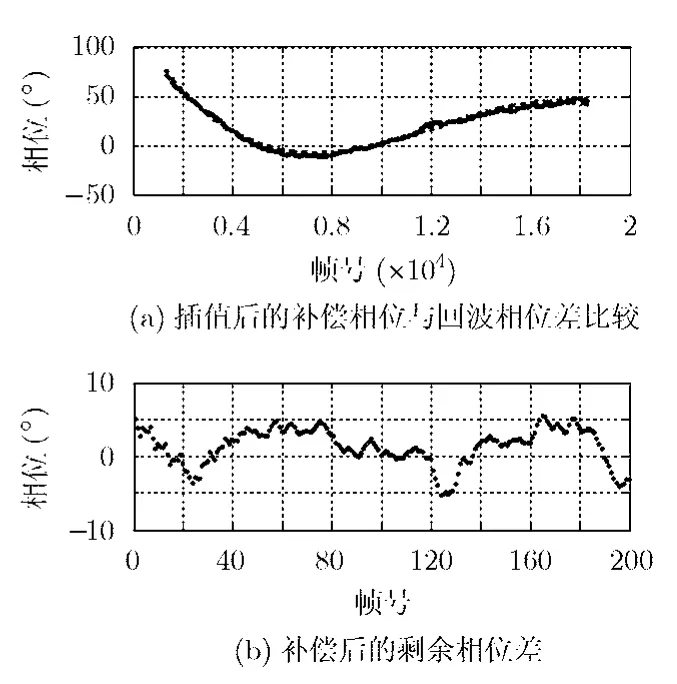
图9 相位同步后的剩余相位误差
参 考 文 献
[1]Bamler R and Hartl P. Synthetic aperture radar interferometry[J].Inverse Problems, 1998, 14(4): R1-R54.
[2]Weiβ M. Time and frequency synchrozisation aspects for bistatic SAR systems[C]. Proceedings of EUSAR, Ulm Germany, 2004: 395-398.
[3]Krieger G and Younis M. Impact of oscillator noise in bistatic and multistatic SAR[J].IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 424-428.
[4]Krieger G, Hajnsek I, Papathanassiou K P,et al..Interferometric synthetic aperture radar (SAR)missions employing formation flying[J].Proceedings of IEEE, 2010,98(5): 816-843.
[5]Younis M, Metzig R, and Krieger G. Performance prediction of a phase synchronization link for bistatic SAR[J].IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 429-433.
[6]Younis M, Metzig R, Krieger G,et al.. Performance prediction and verification for the synchronization link of TanDEM-X[C]. Proceedings of EUSAR, Dresden Germany,2006: 5206-5209.
[7]Krieger G, Moreira A, Fiedler H,et al.. TanDEM-X: a satellite formation for high-resolution SAR interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2007, 45(11): 3317-3341.
[8]刘基余. GPS卫星导航定位原理与方法[M]. 北京: 科学出版社, 2003, 2, 3节.
[9]Brautigam B, Gonzalez J H, Schwerdt M,et al.. TerraSAR-X instrument calibration results and extension for TanDEM-X[J].IEEE Transactions on Geoscience and Remote Sensing,2010, 48(2): 702-715.
[10]Gonzalez J H, Bachmann M, Krieger G,et al.. Development of the TanDEM-X calibration concept: analysis of systematic errors [J].IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 716-726.

