井壁稳定性评价准则分析

冯永存，邓金根，李晓蓉，蔚宝华

（中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

井壁稳定性评价准则分析

冯永存，邓金根，李晓蓉，蔚宝华

（中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

井壁坍塌失稳大多由于井周岩石的剪切破坏造成，而剪切破坏准则的选择是井壁稳定性预测的关键因素。通常使用的Mohr-Coulomb准则和Drucker-Prager准则都存在明显的缺点，致使井壁稳定性预测结果不准确。于是，引进了一种新的破坏准则——Mogi-Coulomb准则。该准则较为合理地考虑了中间主应力对岩石强度的影响，使强度预测结果更加准确。为验证其优势，利用岩石真三轴试验数据对3种准则的强度预测结果进行了对比分析。结果表明：在真三轴应力状态下，Mogi-Coulomb准则预测岩石强度的精度要高于Mohr-Coulomb准则和Drucker-Prager准则，且具有表达简单、使用方便、预测结果准确等优点。因此，建议推广使用Mogi-Coulomb准则预测井壁稳定性。

破坏准则；Mogi-Coulomb准则；中间主应力；真三轴试验数据；井壁稳定性

钻井过程中，井壁失稳问题严重制约着钻井速度，并造成了巨大的经济损失［1］。统计表明，全球每年由井壁失稳造成的经济损失超过1亿美元，甚至可能高达10亿美元［2-3］。钻井实际中，经常遇到的一类井壁失稳问题是脆性地层中的井壁坍塌［4］。井壁坍塌一般为剪切破坏［5］，可以通过井周应力分析结合适当的剪切破坏准则进行预测。而破坏准则的选取是井壁稳定性预测的关键，国内外学者提出了很多不同的破坏准则，但大多存在明显的不足之处，令钻井工程师难以选择。Mohr-Coulomb（M-C）准则是最简单，也是最常用的准则。该准则忽略了中间主应力σ2对岩石强度的影响，然而很多学者通过试验证明，在很多情况下这一影响不能忽略［6-9］。Drucker-Prager（D-P）准则考虑了中间主应力σ2的影响，但是学者们认为该准则预测的岩石强度过高［10-11］。近年来，Al-Ajmi和Zimmerman提出利用Mogi-Coulomb（MG-C）准则分析脆性地层的井壁稳定性［12-16］，但很少有学者对该准则预测岩石强度的准确性进行研究。

为选择出最能反映钻井实际中脆性地层破坏行为的强度准则，根据调研到的前人所作的真三轴试验数据，对3种准则预测岩石强度的准确性进行了对比，为井壁稳定性预测中破坏准则的选取提供了理论依据。

1 岩石剪切破坏准则

岩石剪切破坏准则按其数学表达形式，可分为线性准则和非线性准则；按其是否考虑中间主应力σ2的影响，可分为未考虑σ2影响的“常规三轴”（或“拟三轴”）准则和考虑σ2影响的“真三轴”准则。

M-C准则是一种线性、“拟三轴”准则，可用最大剪应力τmax与有效平均正应力σm，2的关系来表示：

式中：τmax为岩石所受最大剪应力，MPa；σm，2为有效平均正应力，MPa；a，b为材料常数；c为岩石黏聚力，MPa；φ为岩石内摩擦角，°；σ1为最大主应力，MPa；σ3为最小主应力，MPa。

D-P准则是一种线性、“真三轴”准则，可用八面体剪应力τoct与八面体正应力σoct的关系来表示：

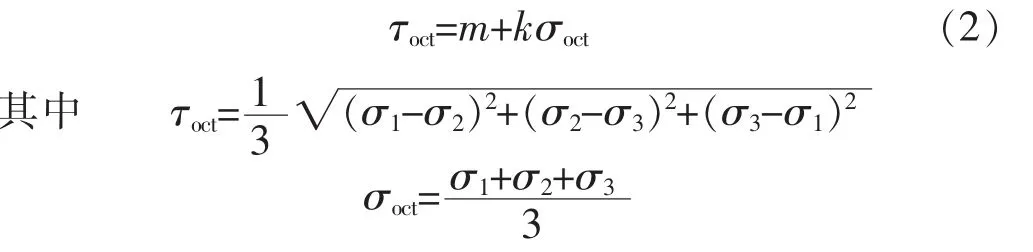
式中：τoct为八面体剪应力，MPa；σoct为八面体正应力，MPa；m，k为材料常数，可由τoct-σoct平面内直线的截距和斜率求得。

Mogi［17］通过试验，一方面证明了中间主应力σ2的确对岩石强度有一定影响，剪切破坏准则中不能忽略σ2对剪切强度的影响；另一方面，还证明了脆性岩石剪切破坏时，破裂面走向总是与σ2的方向相同。因此，Mogi认为作用在剪切破坏面上的应力是有效平均正应力σm，2，而不是八面体正应力σoct，但这并不等同于σ2对岩石强度没有影响。于是，提出了考虑中间主应力σ2影响的Mogi准则：

式中：f为一个单调递增函数，可以是线性函数，也可以是非线性函数。

Al-Ajmi和Zimmerman［15］建议采用Mogi准则的线性形式分析岩石破坏行为，并将线性Mogi准则称为Mogi-Coulomb（MG-C）准则，表达式为

式中：p，q为材料常数。

2 破坏准则对比

实际情况中，井壁围岩应力状态通常为真三轴应力状态（σ1＞σ2＞σ3）。 但是在实验室中，由于设备的限制，一般只能通过常规三轴试验（σ1＞σ2=σ3）来研究岩石的破坏。这样做的假设是，常规三轴试验结果可以代表实际情况中岩石的破坏行为。通常的做法是：先利用常规三轴试验数据对破坏准则进行拟合，再用拟合好的准则来预测真三轴应力状态下的岩石强度。通过以下步骤对上述3种准则的预测精度进行对比：

1）利用常规三轴试验数据，分别在τmax-σm，2，τoct-σoct和τoct-σm，2平面内绘出M-C，D-P和MG-C准则的拟合曲线。

2）利用真三轴实测数σ1，σ2，σ3，根据拟合曲线，计算出τmax和τoct的理论值（预测值）τtmax和τtoct。

3）利用真三轴实测数 σ1，σ2，σ3，根据表达式τmax=计算出τmax和τoct的试验值（实际值）τpmax和τpoct。

4）将真三轴试验数据叠加到各个平面上，观察它们与拟合曲线的吻合情况。

由于现有试验设备难以满足真三轴试验的要求，本文利用的真三轴试验数据均是调研前人的试验结果。文献［12］和［18］中统计了大量自1970年以来，学者们所做的真三轴试验数据。笔者选择了KTB角闪岩、Dunham白云岩、Solenhofen石灰岩、Shirahama砂岩、Yuubari页岩和Westerly花岗岩6组试验数据。

表1给出了M-C，D-P和MG-C准则在6组岩石中的常规三轴试验数据拟合方程，同时给出了预测相对误差Re的平均值。可以看出，M-C准则对6组岩石的预测误差大致在5.2%～7.8%；D-P准则的预测误差较大，基本在10.0%以上；MG-C准则的预测误差值最小，且相对稳定，大致在2.9%～4.3%。

表1 3种准则的拟合公式及预测相对误差

图1—3为3种破坏准则常规三轴试验数据拟合曲线与真三轴试验数据的对比图，由于6组岩石的对比规律大致相同，这里只给出Shirahama砂岩的对比。

图1 M-C准则拟合曲线与真三轴试验数据对比

由图1可以看出，M-C准则拟合曲线位于真三轴试验数据的下方，说明该准则低估了岩石强度，并且随σm，2的增大，试验值τpmax更加偏离理论值τtmax。

图2 D-P准则拟合曲线与真三轴试验数据对比

由图2可以看出，D-P准则拟合曲线位于真三轴试验数据的上方，且偏离较大，说明该准则过高地估计了岩石强度。

图3 MG-C准则拟合曲线与真三轴试验数据对比

由图3可以看出，MG-C准则拟合曲线与真三轴试验数据基本一致，既不像M-C准则低估了岩石强度，也不像D-P准则高估了岩石强度。

3 讨论

地应力是影响井壁稳定性最为关键的因素之一。通常情况下，地应力是非均匀的。在油气钻井所涉及的地层深度内，水平最小地应力与上覆岩层压力之比（σh/σv）通常为0.3～1.5；水平最大地应力和水平最小地应力之比（σH/σh）通常为1.0～2.0［19-20］。 可见，井周岩石在未钻开之前就处于真三轴应力状态（σ1＞σ2＞σ3）下。另外，井眼钻开导致井周出现应力集中，加剧了井周应力的非均匀性。因此，很多学者认为，在分析井壁稳定性时，尤其是在地应力非均匀性较大的地区，中间主应力σ2的影响不能忽略。

地应力非均匀性较大时，M-C准则是不可取的，因为它忽略了σ2的影响，低估了岩石强度，计算的地层坍塌压力过高，降低了钻井信心。而D-P准则虽然考虑了σ2的影响，但它用八面体正应力σoct代替了有效平均正应力σm，2，导致岩石预测强度过高，计算的坍塌压力太低，不具有实际参考意义。Mogi通过试验发现，岩石在剪切破坏前的屈服才是σoct的函数，因此，他认为D-P准则只是一种屈服准则，把它当成剪切破坏准则来用不太合理。由于MG-C准则在预测岩石真三轴强度方面比M-C和D-P准则准确得多，因此有理由认为在实际情况下，尤其是地应力非均匀性较强时，MG-C准则是这3种准则中的首选。

以下讨论常规应力状态（σ1＞σ2=σ3）时MG-C准则与M-C准则的关系。此时，MG-C准则（式（4））退化为

对比式（5）和M-C准则（式（1））可以看出，当σ2＝σ3时，两准则都仅是σ1和σ3的方程，如果取

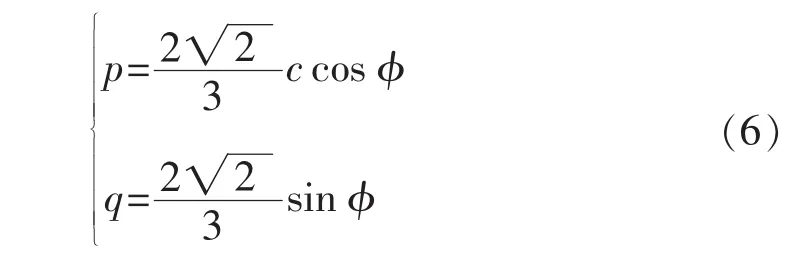
那么，σ2＝σ3时，两准则的形式完全一致，MG-C准则退化为M-C准则。因此，可以认为MG-C准则是MC准则从常规三轴应力状态向真三轴应力状态的推广，后者只是前者的一种特殊情况。

观察式（6），MG-C准则中的系数p，q与M-C准则中的参数c，φ直接相关。这一关系是在常规三轴应力状态下对比得出的。大量试验证实：在常规三轴应力状态下，M-C准则能很好地反映岩石的剪切破坏情况。所以，此时采用式（6）计算p，q是可行的。那么在真三轴应力状态下，是否仍然可以利用式（6）计算系数p，q呢？为此首先利用常规三轴试验数据，根据M-C准则计算出c，φ，然后利用式（6）计算出p，q，代入MG-C准则预测真三轴应力状态下的岩石强度，预测结果与表3中的结果极为相近。因此不论在何种应力状态下，式（6）都是成立的。

2个准则的系数相关这一特点给MG-C准则的使用提供了极大方便。由于试验设备的限制，通常只能进行常规三轴试验。但有了式（6）所表示的系数相关关系，可以利用常规三轴试验数据直接对MG-C准则进行拟合；还可以先根据常规三轴试验数据确定M-C准则中的参数c，φ，然后根据式（6）确定MG-C准则中的系数p，q。更重要的一点是，可以利用测井资料确定连续地层段上的 c，φ值［21］，进而根据式（6）确定 p，q，得到整个地层段上的MG-C准则，从而对地层强度进行连续预测。

4 建议

近年来，Al-Ajimi和 Zimmerman等人开始利用MG-C准则建立井壁稳定性预测模型，并在澳大利亚的Wanaea油田、印度尼西亚的Pagerungan岛气田、英国的Cyrus油田及阿拉伯湾等地区进行了实际应用，均取得了令人满意的效果。而国内迄今为止还未见有使用MG-C准则预测井壁稳定性的报道，鉴于M-C准则和D-P准则存在的诸多缺点，以及国外成功使用MG-C准则预测井壁稳定性的范例，建议国内推广使用MG-C准则预测脆性地层的井壁坍塌失稳。

5 结论

1）中间主应力σ2对岩石强度有一定影响，尤其在地应力非均匀性较强的地区，σ2对井壁稳定性的影响不能忽略。

2）M-C准则没有考虑σ2对岩石强度的影响，低估了岩石强度，井壁稳定性预测结果过于保守；D-P准则用八面体正应力σoct代替了有效平均正应力σm，2，导致岩石预测强度过高，井壁稳定性预测结果过于乐观。

3）MG-C准则适当地考虑了σ2对岩石强度的影响，岩石强度预测精度比M-C准则和D-P准则高得多，特别适合在地应力非均匀性较强的地区使用。在常规三轴应力状态下MG-C准则退化为M-C准则，可以看成MG-C准则是由常规应力状态向真三轴应力状态的延伸。MG-C准则表达简单，并且它的系数与M-C准则中参数的c，φ有简单的相关关系，极大地方便了该准则的使用。

［1］杨振杰，李家芬，苏长明，等.井壁加固技术研究进展［J］.断块油气田，2008，15（3）：99-102. Yang Zhenjie，Li Jiafen，Su Changming，et al.Advances in side wall strengthening technology［J］.Fault-Block Oil&Gas Field，2008，15（3）：99-102.

［2］Al-Ajmi A M，Sultan Qaboos U，Zimmerman R W.Stability analysis of deviated boreholes using the Mogi-Coulomb failure criterion，with applications to some oil and gas reservoirs［A］.SPE 104035，2006.

［3］朱荣东，陈平，夏宏泉，等.裂缝井壁力学稳定性研究［J］.断块油气田，2007，14（5）：56-58. Zhu Rongdong，Chen Ping，Xia Hongquan，et al.Study on stability of fractured borehole wall［J］.Fault-Block Oil&Gas Field，2007，14（5）：56-58.

［4］谭强，邓金根，张勇，等.各向异性地层定向井井壁坍塌压力计算方法［J］.断块油气田，2010，17（5）：608-610. Tan Qiang，Deng Jingen，Zhang Yong，et al.Calculation method of directional borehole collapse pressure in anisotropic formations［J］. Fault-Block Oil&Gas Field，2010，17（5）：608-610.

［5］邓金根，张洪生.钻井工程中井壁失稳的力学机理［M］.北京：石油工业出版社，1998：30-33.Deng Jingen，Zhang Hongsheng.Mechanical mechanism of wellbore instability during drilling［M］.Beijing：Petroleum Industry Press，1998：30-33.

［6］Takahashi M，Koide H.Effect of the intermediate principal stress on strength and deformation behavior of sedimentary rocks at the depth shallower than 2，000 m［C］.Pau：International Society for Rock Mechanics，1989.

［7］Haimson B C，Chang C.A new true triaxial cell for testing mechanical properties of rock，and its use to determine rock strength and deformability of Westerly granite［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37（1）：285-296.

［8］Haimson B C，Chang C.True triaxial strength of the KTB amphibolite under borehole wall conditions and its use to estimate the maximum horizontal in situ stress［J］.Journal of Geophysical Research：Solid Earth，2002，107（B10）：2257-2271.

［9］Song I，Haimson B C.Polyaxial strength criteria and their use in estimating in situ stress magnitudes from borehole breakout dimensions［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（3/4）：498.

［10］McLean.M R，Addis M A.Wellbore stability analysis：A review of current methods of analysis and their field application［A］.SPE 19941，1990.

［11］Santarelli F J.Theoretical and experimental investigation of the stability of the axisymmetal wellbore［D］.London：University of London，1987.

［12］Al-Ajmi A M，Zimmerman R W.Relationship between the parameters of the Mogi and Coulomb failure criterion［J］.International Journal of Rock Mechanics and Mining Sciences，2005，42（3）：431-439.

［13］Al-Ajmi A M，Zimmerman R W.Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion［J］.International Journal of Rock Mechanics and Mining Sciences，2006，43（8）：1200-1211.

［14］Al-Ajmi A M，Zimmerman R W.A new 3D stability model for the design of non-vertical wellbores［A］.ARMA 06-961，2006.

［15］Al-Ajmi A M，Zimmerman R W.The Mogi-Coulomb true-triaxial failure criterion and some implications for rock engineering［M］.London：Taylor&Francis Ltd.，2007：475-479.

［16］Islam M A，Skalle P，Al-Ajmi A M，et al.Stability analysis in shale through deviated boreholes using the Mohr and Mogi-Coulomb failure criteria［A］.ARMA 10-432，2010.

［17］Mogi Kiyoo.Fracture and flow of rocks under high triaxial compression［J］.Journal of Geophysical Research，1971，76（5）：1255-1269.

［18］Colmenares L B，Zoback M D.A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks［J］.International Journal of Rock Mechanics and Mining Sciences，2002，39（6）：695-729.

［19］Chen X，Tan C P，Haberfield C M.A comprehensive，practical approach for wellbore instability management［A］.SPE 80146，2002.

［20］Tan C P.An analytical method for determining horizontal stress bounds from wellbore data［J］.International Journal of Rock Mechanics and Mining Sciences，1993，30（7）：1103-1109.

［21］陈勉，金衍，张广清.石油工程岩石力学［M］.北京：科学出版社，2008：299-305. Chen Mian，Jin Yan，Zhang Guangqing.Petroleum engineering related rock mechanics［M］.Beijing：Science Press，2008：299-305.

（编辑 赵卫红）

Analysis of failure criterions on wellbore stability prediction

Feng Yongcun,Deng Jingen,Li Xiaorong,Wei Baohua
(MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing 102249,China)

Wellbore collapse is mostly caused by the shear failure of the rock around borehole.One of the key considerations on wellbore stability prediction is the choice of shear failure criterion.The commonly used Mohr-Coulomb and Drucker-Prager failure criterions have obvious shortcomings,which leads to the unrealistic predicting results.Therefore,a new failure criterion,Mogi-Coulomb criterion,is introduced in this paper.The advantage of this criterion is that it properly evaluates the effect of intermediate principal stress on rock strength,thus it has more accurate prediction result.In order to present its advantage,the prediction results of rock strength predicted by the three criterions above are compared based on true triaxial test data.The results indicate that,under true triaxial stress state,it is more precise to predicate rock strength using the Mogi-Coulomb criterion rather than using the Mohr-Coulomb and Drucker-Prager failure criterions.In view of the advantages of the Mogi-Coulomb criterion,such as simple expression, easy to use and high prediction accuracy,it is highly recommended to use the shear failure criterion in the analysis of future wellbore stability.

failure criterion;Mogi-Coulomb failure criterion;intermediate principal stress;true triaxial test data;wellbore stability

国家科技重大专项“大型油气田及煤层气开发”子课题“煤层气钻井工程技术及装备研制”（2008ZX05036）

TE21

：A

1005-8907（2012）02-0244-05

2011-08-20；改回日期：2012-01-13。

冯永存，男，1986年生，在读硕士研究生，2009年毕业于中国石油大学（北京）石油工程专业，主要从事石油工程岩石力学研究。电话：（010）89733911-18，E-mail：yongcun_feng@163.com。

冯永存，邓金根，李晓蓉，等.井壁稳定性评价准则分析［J］.断块油气田，2012，19（2）：244-248. Feng Yongcun，Deng Jingen，Li Xiaorong，et al.Analysis of failure criterions on wellbore stability prediction［J］.Fault-Block Oil&Gas Field，2012，19（2）：244-248.