最小二乘法修正管线探测埋深分析与应用

胡应清，江周勇

(重庆市勘测院，重庆 400020)

最小二乘法修正管线探测埋深分析与应用

胡应清∗，江周勇

(重庆市勘测院，重庆 400020)

管线探测埋深修正一直是管线探测者的难题，本文提出了利用数学上的最小二乘法来修正管线探测埋深。最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳匹配函数。管线探测埋深和部分通过开挖手段获取的实际埋深可以看成一系列数据组，利用最小二乘法，获取这些数据组的最佳匹配函数，求取未知点的实际埋深。本文基于以上思路，通过理论研究和实践应用来分析该方法的可行性。

管线探测埋深；埋深修正；最小二乘法

1 引 言

城市地下管线探测工程中，隐蔽管线点埋深最常用的探查方法是电磁法，即使用专业的管线探测仪，用发射机给目标管线施加某种高频电磁信号，利用接收机接受目标管线的信号，并分析其变化规律，从而实现对目标管线定深。目前，国内外流行的管线探测仪(如RD4000、LD6000、富士PL－960等)对目标管线进行测深时，都要求探测者在已知区域进行方法试验，确定修正系数。但现实管线探测工程中，目标管线的地球物理环境千差万别，管线埋深也不一致，探测深度与管线的实际埋深有一定的出入，这种出入的大小也不固定。为了得到最接近实际的埋深，本文提出了一种管线探测埋深修正方法。

2 最小二乘法原理

最小二乘法可以用来处理一组数据，可以从一组测定的数据中寻求变量之间的关系，这种函数关系也通常称为经验公式。假定两变量x、y之间近似呈线性关系，实验测定n组数据，(x1，y1)、(x2，y2)、……、(xn，yn)，这n组数据在平面上可以展绘出n个点(xi，yi)，这些点大致分布在某直线附近，我们称x、y近似为一线性函数，定义为y＝ax＋b，a、b为待定常数。记Ei＝yi－axi－b，它反映了用直线y＝ax＋b描述点列(xi，yi)单个偏差的大小。最小二乘法运用来度量总偏差的大小，即通过确定线性函数y＝ax＋b中的常数a和b，使取值最小。由极值原理得即:

解上述方程得:

3 最小二乘法修正管线探测埋深的实现

电磁法探查目标管线埋深的理论依据是电磁场理论，通常都是通过在地面测定目标地下管线在一次场作用下，感应电流产生的二次场的变化来确定目标地下管线的空间位置。理想情况下，较平直的管线产生的交变电磁场，可以看成无限长直导线产生的电磁场，根据比奥－萨法尔定理，在地面上离开管线中心距离r处的磁场强度(H)为:

式中，I为流经管线的交变电流；

r为管线中心至地面某点的距离；

K为常数，大小为

图1 管线探测与埋深关系示意图

在管线探查工程中一般都是通过测定管线在地表产生的水平分量或垂直分量，根据其变化规律来确定管线在地表的平面位置和中心埋深，在磁偶源发射条件下，目标管线中产生感应电流大小为:

式中，C为常数，与发射线圈的大小、形状、匝数、材料等参数有关；α为线圈面法线方向和二次场方向之间的夹角。

在实际工程中，最常用的发射方式有两种，即:

水平发射线圈，此时目标管线中的感应电流为:

当线圈处于目标管线在地面的投影位置O处(x＝0)，垂直线圈与目标管线无耦合，水平线圈与目标管线有最佳耦合，则有:

在实际管线探查中，用某种探查方法探查的目标管线埋深(未修正)我们姑且称之为视埋深，记为h′，管线的实际埋深记为h。探查埋深误差与管道埋深相关，这种关系可以近似表示为比例关系。同时，管线探测工作中，视埋深h′一般为管线视中心埋深，规范要求所求埋深一般是管顶埋深，特别对管径较大的管道，视中心一般不是管道断面的几何中心，不能简单地通过减掉管道半径求取管顶埋深。不同的地球物理环境，也会造成视埋深h′与实际埋深h相差某个常数。

综上所述，实际埋深h可以近似地用视埋深h′的一次多项式拟合，即表示为:

式中，a，b为某一常数。

某些重点管道探测工程中，通过明显点方法实验或开挖、钎探总能够获得部分目标管线点(设共有m个，m>2)实际埋深hi，同时这些点全部探查有视埋深h′i，这些点记为(h′1，h1)、(h′2，h2)、……、(h′m，hm)，称为管线埋深校正点。分别代入上式，得:

运用最小二乘法，求解上述方程组，求取常数a、b的值，得:

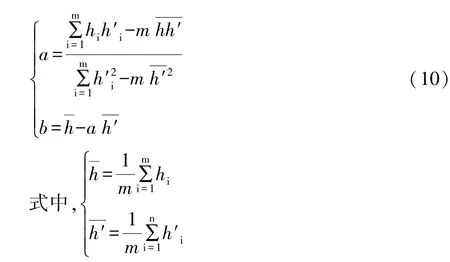
为保证修正参数的正确性，管线埋深误差满足规程要求，可以做如下检验。

第一，多个管线校正点中选取至少1个点不参与埋深修正参数计算，把该点作为修正检校点，记为(h′k，hk)。当Ek＝｜hk－ah′k－b｜值小于0.15hk，校正合格。

第二，记Ei＝｜hi－ah′i－b｜，当某个Ei＝｜hi－ah′i－b｜值大于0.15hi，剔除该点，重新用剩下的点计算常数a、b的值，直至Ei＝｜hi－ah′i－b｜全部小于0.15hi。

这样，通过检验，最终计算的常数a、b值代入式(8)，就可以修正其他点视埋深了。

4 工程实例

在某新建立交桥场地施工管线探测工程中，场地内有一根DN1400钢质给水管道穿越，管道埋深处于1 m～3 m之间，全长约1.6 km，中间区域有一检修井，其余部分为埋地管道。管道穿越处地球物理条件基本相同，均为回填土。场地部分区域不利于开挖，施工方需要管道准确埋深，以便确定施工方案。

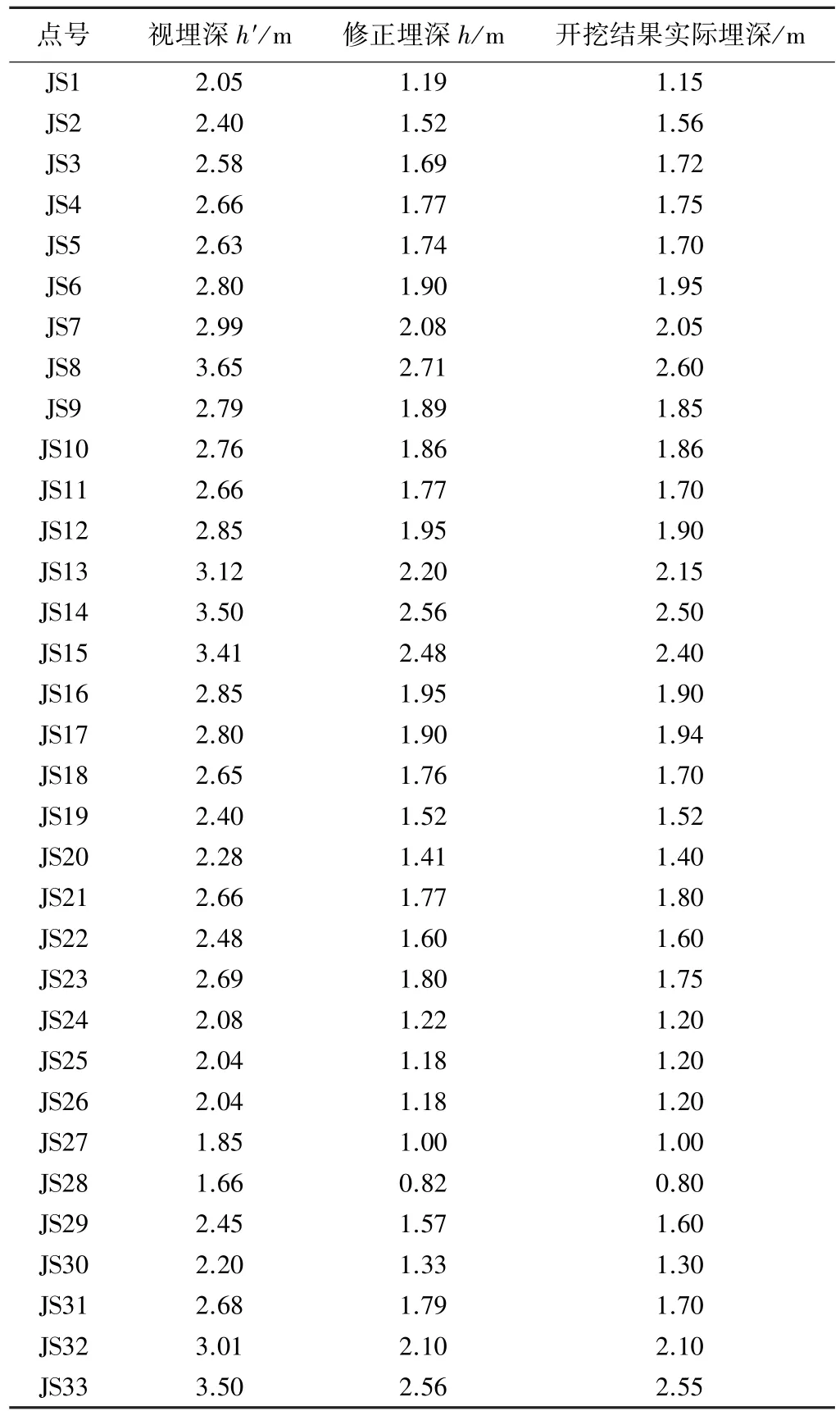
初始探测时，在管线中部检修井处使用直连法给管线施加信号，探测发现仅能探查100 m远，信号就消失，只能采用感应法继续探测。共探测管线点33点，每点采用相同的探测方法求取埋深，开挖6点，获取其实际埋深，数据如表1所示。

埋深修正实例 表1

将点号为JS2、JS10、JS19、JS28、JS33的管线点实际埋深和探测埋深(点号为JS17的管线点作为修正检校点，不参与修正参数计算)代入式(9)得:

Ei＝hi－ah′i－b全部小于0.15hi(i＝2，10，19，28，33)，合格。

得到管线埋深修正公式:

根据式(12)，管线点修正埋深见(表1)。工程后期，管线全部开挖验证表明(开挖验证结果如表2所示)，修侧结果完全满足规程要求。

管线开挖验证结果 表2

5 结 论

本文所述的管线探测埋深修正方法，特别适用于管径较大的单一管道探测，修正后的管线埋深非常接近管线的实际埋深。不足之处，在于必须有部分管线点利用开挖或钎探验证能得到实际埋深，以便能进行修正。

参考文献

[1] CJJ61－2003.城市地下管线探测技术规程[S].

[2] 同济大学应用数学系.高等数学[M].上海:同济大学出版社，2008.

[3] 黄云清，舒适，陈艳萍等.数值计算方法[M].北京:科学出版社，2010.

[4] RISN－TG011－2010[S].城市地下管线探测工程监理导则.

[5] 区福邦.城市地下管线普查技术研究与应用[M].南京:东南大学出版社，1998.

Analysis and Application of the Least Squares Method to Fix the Pipeline Detection Depth

Hu Yingqing，Jiang Zhouyong
(Chongqing Surver Institute，Chongqing 400020，China)

Pipeline detection depth correction has been the problem of pipeline detection，this paper proposes a method－the clever use of the mathematical least squares method to fix the pipeline detection depth.The least squares method is a mathematical optimization techniques by minimizing the sum of the error squares to find the best matching function of the data.The pipeline probing depth and partial excavation means to obtain the actual depth can be seen as a series of data sets，using the least squares method to obtain the best matching function for these data sets，to strike the actual depth of the unknownpoint.Based on the above ideas，through theoretical study and practical application to analyze the feasibility of this method.

The pipeline detection depth；Depth correction；Least squares method

2012—02—09

胡应清(1978—)，男，工程师，主要从事城市工程物探和工程测量方面的技术工作。

1672－8262(2012)05－151－04

P631.3＋3，TU990.3

B