某雷达天线座稳速控制精度改进设计

李宝龙 张永梅

(西安电子工程研究所 西安 710100)

1 引言

车载搜索雷达一般具有多平台装载、机动性能好等特点。典型的装载方式为搜索雷达直接安装在载体上，搜索雷达随载体可以全方位旋转;同时，为了满足机动性能的要求，在搜索雷达工作过程中需要抵消载体姿态变化带来的影响。由于该搜索雷达为相控阵雷达，当载体姿态变化时，可以通过相位扫描方式来补偿俯仰上的变化量，而方位上的变化量则需要伺服控制来补偿，即保证方位运转的匀速性。所以，必须对搜索波束的方位运转速度进行稳定，使波束的方位扫描速度在大地坐标系中始终保持匀速，因此，提高搜索雷达天线座方位转速的稳定性就成为伺服分系统研究的主要问题。

2 影响天线座伺服分系统稳速特性的因素分析

2.1 干扰力矩分析

直流力矩电动机系统具有良好的控制特性、大的峰值力矩和高可靠性等优点，因而在高精度速率和位置伺服系统中得到了广泛的应用，但是各种干扰力矩的存在影响着系统的速率和位置精度。由控制理论可知，加入积分校正的系统可以对常值力矩干扰有效抑制，但对电机波动力矩抑制能力不够。从结构上讲，电机波动力矩主要包括齿槽波动力矩和电磁波动力矩两种。通过采用磁极错位、齿极合理配合以及分数槽绕组的结构，使齿槽力矩被抑制在一个很低的水平，特别是本文所述系统采用的是III型系统，齿槽力矩引起的转台角速率波动的绝对值和相对值都较小。因此电磁力矩波动成为抑制的重点。

在理想状态下，转子采用高电阻率、低磁导率的稀土永磁磁钢，转子上的感应电流可以忽略。若同时忽略饱和、涡流等影响，电机的电磁力矩可以表示为:

式中:P为电机极对数;ωe为电机电气角速度;且ωe= Pωr、ωr为机械角速度;m为电机相数;ej为第j相的反电势;ij为第j相的反电流。

若设电动机的反电势及相电流波形均为正弦形状，则有:

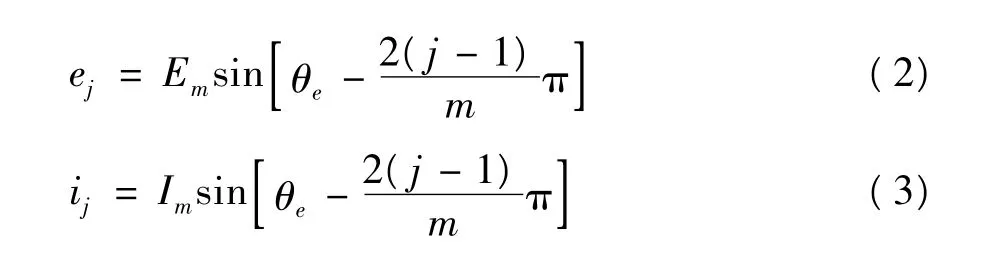
式中Em、Im分别为反电势、相电流幅值。

速率转台伺服控制系统结构框图如图1所示，其中r(s)表示输入位置指令;TL表示折算到电机轴上的扰动力矩(主要包括摩擦力矩和波动力矩);u1表示位置环控制器输出;u2为速度环控制器输出;R为绕组等效电阻;L为绕组等效电感;KT为电机力矩系数;Ke为电机反电势系数;Kc为电流环控制器等效增益;τ 为惯性环节时间常数。

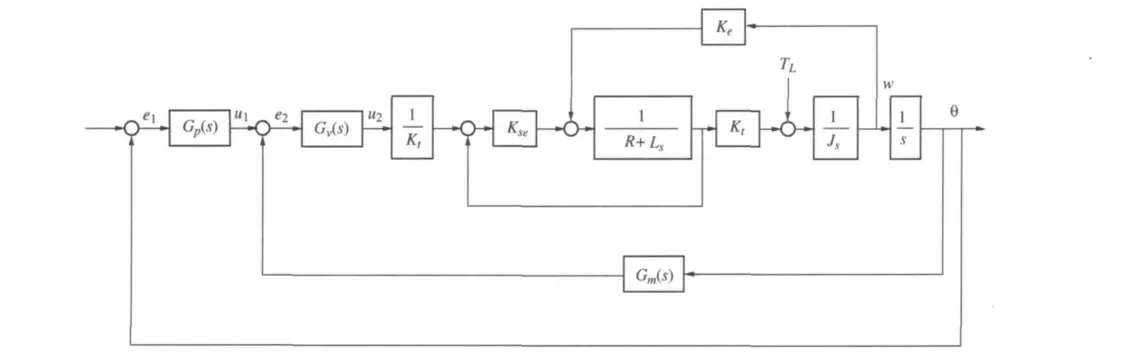
图1 速率伺服控制系统结构框图

考虑位置环控制器的输出:

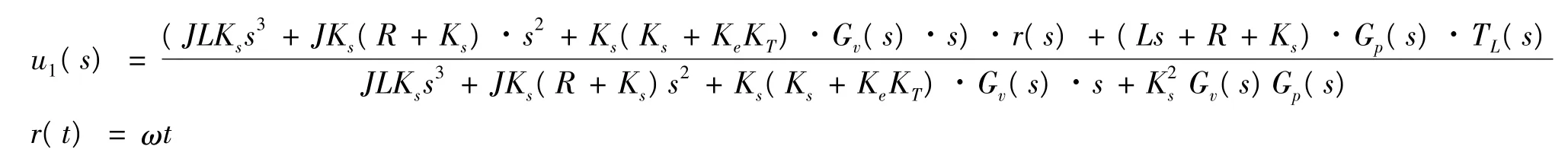
当输入指令，其中ω 为角速度，则r(s)=ω/s2。系统运行进入稳态时，不考虑干扰力矩TL(s)的影响，根据中值定理，则控制器的输出u1=(Ks+KeKT)/Ksω，ω 为常值，所以折算到电机轴上的扰动力矩可以由u1来反应。

在速率伺服系统中，有刷直流电机系统的角速度是一个被测量，可以得到速率波动Δω 和波动力矩［Tv-T］的关系:

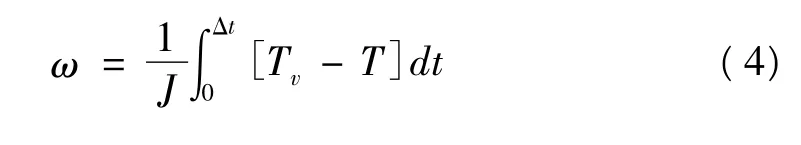
根据所建立的波动力矩的数学模型，可以得到对应某一频率成分的电机波动力矩引起转速波动Δω 的相对值为:

式中:ω 为机械角速率;γ= vP为每机械圆周波动力矩的波动次数，v=1，2，3，…，n;Tv为vP次波动力矩的幅值;P为电机极对数;J为系统惯量;T为平均力矩;Δt为表示波动力矩周期。

2.2 与光纤陀螺相关的误差分析

本系统通过光纤陀螺作为系统速度环的主要反馈元件，因此，由光纤陀螺提供的反馈信号的好坏直接影响速率伺服系统精度的好坏。反馈元件的误差是一种有规律的误差，这将引起天线座产生有规律的速度波动，但是由于这种误差产生于反馈回路上，因而这种速度误差不能通过改变控制系统的参数来消除或减小，需要通过数值补偿算法减小光纤陀螺的自身误差，是提高系统精度的关键。

静基座上，陀螺的量测轴垂直于水平面，实际测量某一光纤陀螺的输出为:

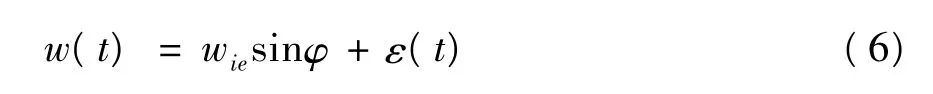
其中，wie为地球自转角速率，φ 为测试点的地理纬度，ε(t)为陀螺漂移。陀螺漂移由常值分量、周期分量和白噪声组成，即:

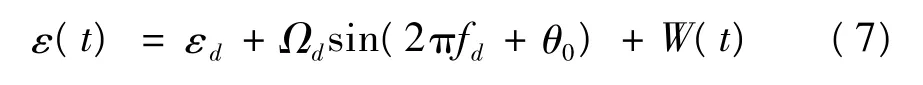
其中，εd为零偏，短时间内近似为一个常数;Ωd为周期分量的幅值;fd为周期分量的频率;θ0为初始相位;W(t)为陀螺噪声。图2 是光纤陀螺的典型结构和相关误差源。造成光纤陀螺噪声W(t)过大的主要误差源有以下几种:

A.克尔效应:克尔效应是一种非线性光学效应。当陀螺光纤环中两束反向传输光波的功率不同时，会引起各自传播常数的不同，导致非互易相位误差，寄生在Sagnac 相移中，对光纤陀螺的偏置稳定性有影响;

B.背向瑞利散射:瑞利散射归因于光纤内部介质密度或应力不均匀而导致的折射率不均匀性。位于光纤环中心一段长为Lc(光源相干长度)的光纤产生的瑞利散射波和主波干涉，会引起不可忽略的漂移量，影响光纤陀螺的偏置稳定性;

C.法拉第磁场效应:光纤陀螺中光波的偏振状态受地磁场影响而发生变化，这种变化与光的传播方向有关，称之为法拉第效应;

D.光路中的偏振噪声:在光纤陀螺中，偏振器的不理想、光纤线圈的偏振交扰，以及其它器件的偏振波动效应等对光纤陀螺的偏置稳定性影响很大;

E.信号检测误差:

a.随机噪声，如前放噪声、乘法检波噪声、输出放大误差;

b.电路参数设计与实现因素，如开环增益，采样和控制频率等;

c.闭环系统校正网络参数设计和系统带宽、稳定裕度等。

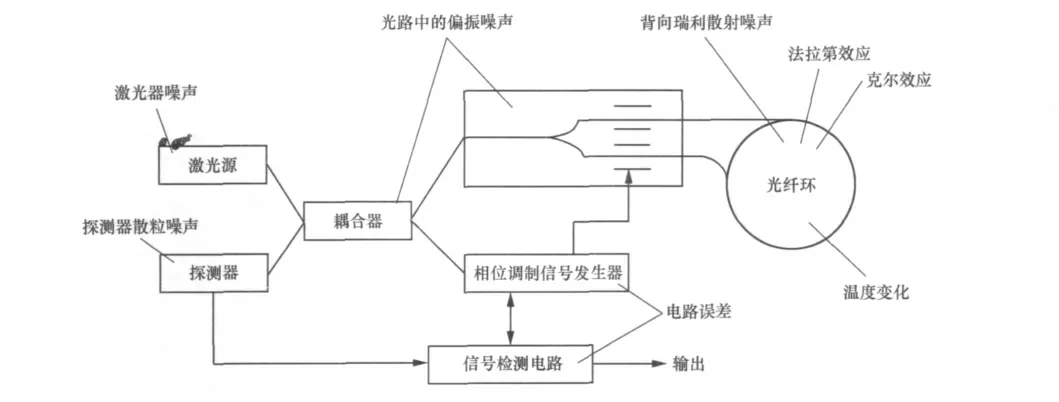
图2 光纤陀螺的典型结构和相关误差

3 天线座稳速伺服分系统设计

3.1 基于重复控制的高精度速率伺服控制系统设计

针对之前对电机电磁波动力矩的分析，以及电磁波动力矩的数学模型，可以采用插入式重复控制器来解决。采用这种结构的优点是:原始控制器的设计和重复控制器的设计相互独立，对于一些没有采用重复控制方法的系统，不必对控制器进行任何修改而仅需增加一个相加环节，就可以将重复控制器加入原系统中，从而大幅度地提高系统的稳态精度。图3 为插入式重复控制器典型框图，关于这类重复控制系统的设计问题，目前已有一些文献给出了设计方法［4］。

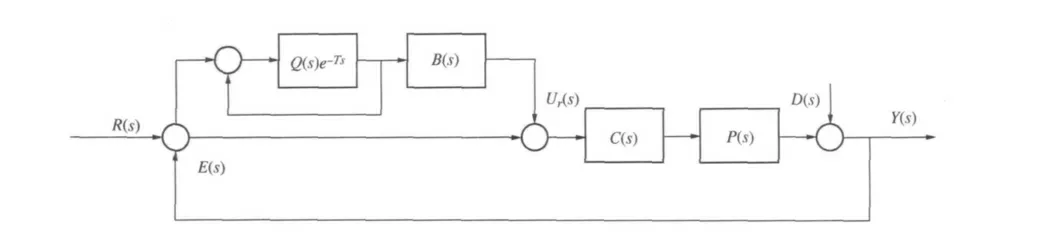
图3 插入式重复控制系统框图

其中R(s)、E(s)、D(s)、Y(s)分别为参考信号、误差信号、扰动信号和系统输出;Ur(s)为重复控制器输出;C(s)、P(s)分别为原始控制器和被控对象的传递函数，一般称G(s)= C(s)P(s)为广义被控对象;Q(s)、B(s)分别为低通滤波器和动态补偿器。

重复控制系统的设计指标分为稳态和暂态两部分，设原始系统的灵敏度函数为So(s)，加入重复控制器后系统的灵敏度函数为Sr(s)，则要求有:

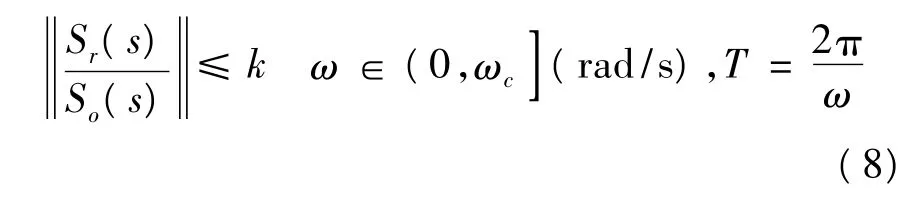
除此之外，则需要系统重构谱的峰值小于并接近于1，以保证系统有一定的稳定裕度并有较好的暂态特性。这里指定暂态性能指标为:

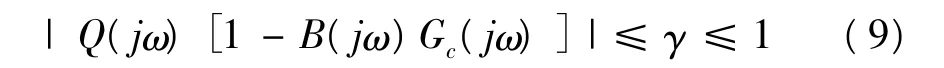
现有的插入式重复控制方法采用先设计低通滤波器Q(s)，然后设计动态补偿器B(s)的方式。这样的设计方式带有较大的保守性。为了减小设计的保守性，采用下面的方法，其设计步骤为:

a．根据系统暂态指标(8)要求以及所选定的低通滤波器的结构形式，确定B(s)带宽并进一步确定其参数。

b．选择Q(s)以保证系统的稳态性能。

实际的机电伺服系统具有低通的特性，在中、低频段可以得到:

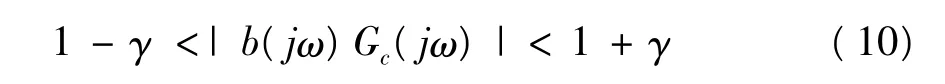
所以只需要对b(jω)Gc(jω)进行相角补偿，就可以使式(9)成立，其补偿条件为:

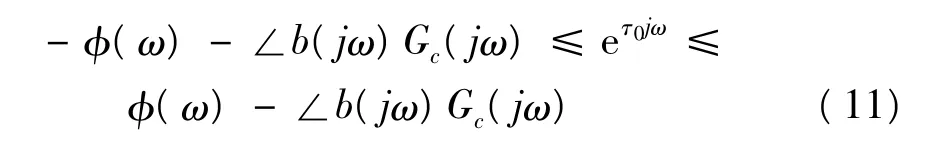
通过求满足(11)式的τ0值，就可以确定一个合理的超前相角补偿系数，为便于在实际系统中应用，b(s)取为的形式，其中T的数值由重复控制器的带宽ωc确定。

低通滤波器的设计也就是在式(8)的条件下Q(s)的形式和参数选择问题，由一个低通滤波器q(s)和一个线性相位超前补偿eτ1s组成。其中q(s)为有理真分式形式，根据实际应用的特点，选择q(s)具有:

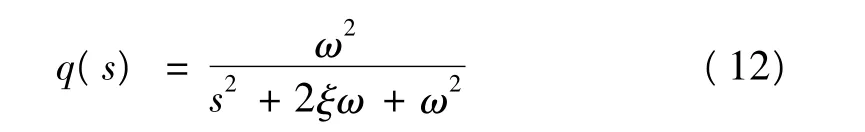
其中ξ=0.707。

为了得到比较理想的超前补偿系数，取:

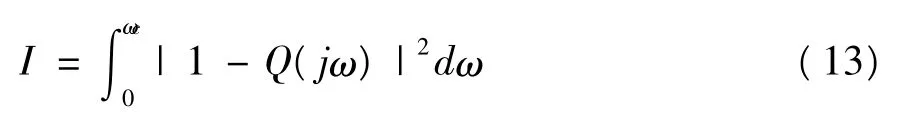
为指标函数对τ1进行优化，当I的值越小时，系统抑制干扰，跟踪输入指令的效果越好，从而求得理想的超前补偿系数。

3.2 陀螺信号处理

速率陀螺作为速度闭环的反馈测量元件，是确保控制效果的关键一环，而其输出信号精度却受到自身零点漂移和外界环境干扰等很多因素的影响。为了提取有用的信号，保证稳定环路的输出精度，必须对陀螺输出信号进行滤波预处理。由于陀螺信号噪声具有不稳定性和随机性的特点，采用传统以傅里叶变换为核心的数字滤波算法并不能收到好的效果。因此，本系统采用了小波阈值去噪滤波算法，同时在对小波系数估计中，采用了软、硬阈值折中的方法，收到了比一般软阈值或硬阈值好的效果。其主要实现步骤如下:

a.对陀螺输出信号ω(t)进行小波变换，得到一组小波系数dj，k。设信号离散采样后得到N点离散信号ω(n)，其小波变换为:

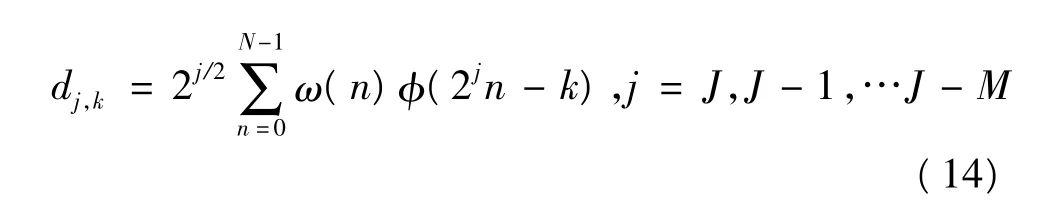
由于式(14)的计算量比较大，且φ(t)一般没有显示表达式，因此运算时采用Mallat 快速分解算法，可以得到简化的小波变化递归实现方法:

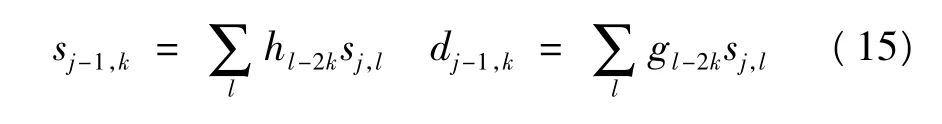
其中，h和g分别为对应于尺度函数和小波函数的低通和高通滤波器，{sj，k}k∈Z为不同尺度空间下的尺度系数。

b.对小波系数dj，k进行阈值处理，得到一组新的估计小波系数(EWC)，阈值估计方法采用软、硬阈值折中法，其规则为:

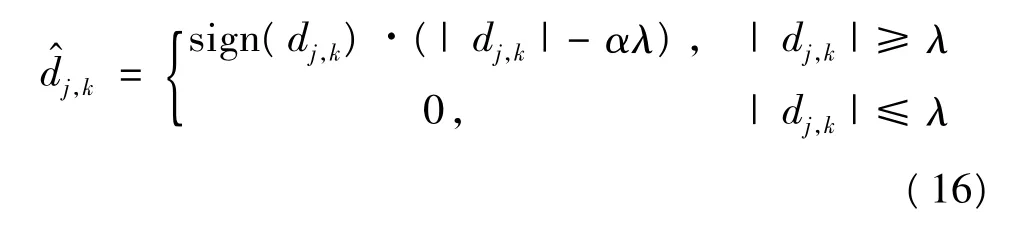
其中，λ 是阈值;α 为调节因子，且0 ≤α ≤1。由上式可知，当α=0 时，原式即为硬阈值估计法，其缺点为:在λ 处不连续，因此利用重构的信号会产生振荡;当α=1 时，原式即为软阈值估计法，其缺点为EWC的绝对值总比原系数小λ，造成重构信号与真实信号之间有固定偏差。而由式(16)估计所得的介于|dj，k|-λ 与|dj，k|之间，使得EWC更趋近于真实值，因此只要适当选择α 的大小，就可获得很好的去噪效果。

c．最后，由EWC 进行小波重构，得到估计信号即为去噪后的信号。小波重构递推公式为:

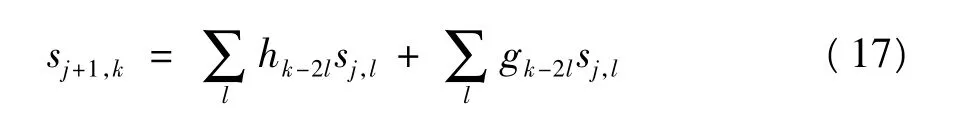
实际应用时，以10 ms 为周期进行一次解算，小波滤波器采用了Daubechie-5 小波基，分解最大尺度选为6 级，阈值λ 采用了Stein 无偏风险估计准则(sure 阈值)，这样每一尺度上的阈值不同，有利于减小计算误差。

图4 为光纤陀螺输出的同一组数据进行了小波滤波输出效果图。可以看到，原始信号中有许多毛刺儿，明显地受到了噪声干扰。从图中可以看出小波阈值滤波方法有效的去除了噪声信号，保留了有效信号。经过滤波，陀螺原始信号方差可降至45%左右。虽然理论上小波滤波算法中的分解尺度越大，滤波效果越好，但是在实验中发现，尺度越大，计算量越大，势必造成计算误差增大，也会使计算输出时间增大，造成实际应用效果反而不好。因此实际应用中，应该在保证目标精度的前提下，尽量减小计算量，选用合适的分解尺度。此外，滤波算法中调节因子α 的选择也影响到小波滤波效果的好坏，经过多次试验，α 为0.5 时可以获得较好的效果。

图4 小波去噪效果图

4 系统测试结果

当系统设定为180°/s 运转时，设计20ms 一个周期的采样周期，通过对转台编码增量的计算，即每20ms 时，实际编码增量相对与60mil 增量的误差，图5 显示了采用上述措施前后编码误差。结果显示，实现了系统稳速目标，改善了系统稳速的稳定性、且保持了较高的稳速精度。其稳速精度在2%以内。

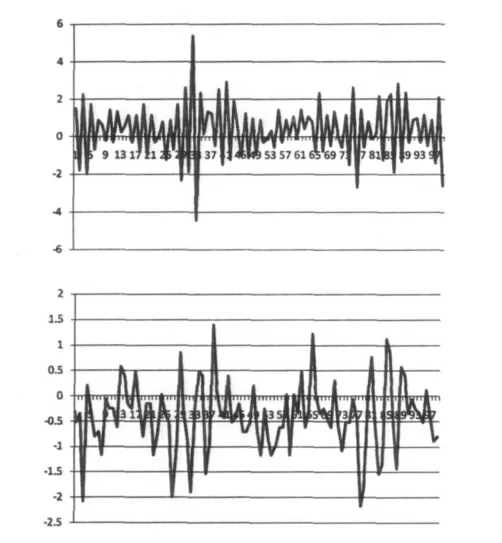
图5 采用措施前后编码误差

5 结论

本文针对影响天线座稳速稳定性的原因，根据转台系统的实际工作情况，提出了基于插入式重复控制方案，并且采用优化过的重复控制设计方法，重复控制器中的低通滤波器Q(s)和动态补偿器B(s)都易于实现，实用性强。同时，采用对速率陀螺的反馈信号进行信号滤波预处理，很好地去除了噪声，并且真实地反映了信号的边界和趋势，实现了信噪分离。有效的解决了某雷达在批量生产过程中出现天线座方位运动速度稳定性差、精度低等问题。

［1］叶自清.船载天线自动跟踪系统测控技术研究［J］.中南林学院硕士学位论文，2003.10.

［2］候志强，王祖林.车载天线定向系统设计［J］.电子测量技术，2006，8，29(4).

［3］夏承光，肖锦等.位置伺服系统的学习控制研究［J］.自动化学报，1992.

［4］师黎，孔全生.反馈控制系统导论［M］.北京:科学出版社，2005:20-33.

［5］张智永.移动载体稳定跟踪平台测控技术研究［D］.长沙:国防科学技术大学，2002.

［6］徐邦荃，李浚源，詹琼华.直流调速系统与交流调速系统［D］.武汉:华中科技大学出版社，2000:35 ～39.

［7］Fourati W，Kammoun F，Bouhlel M S.Medical image denoising using wavelet thresholding［J］.Journal of Testing and Evaluation，2005，33(5):364-369.

［8］周涌.非线性系统的神经网络内膜控制研究［D］.南京理工大学博士学位论文，2003，33-35.

［9］龚晓风，高矜畅，周春晖.时滞系统PID 控制器内模整定方法的扩展［D］.控制与决策，1998，13(4):337-341.